NCERT Solutions for Class 9 Maths Chapter 9 - Exercise 9.1 Areas of Parallelograms and Triangles
Q1. Which of the following figures lie on the same base and between the same parallels.
In such a case, write the common base and the two parallels.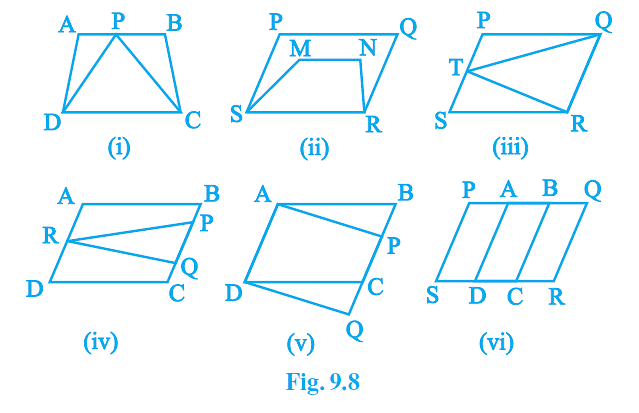
Ans: The figures (i), (iii), and (v) lie on the same base and between the same parallels.
| Common base | Two parallels | |
| Fig. (i) Fig. (iii) Fig. (v) | DC QR AD | DC and AB QR and PS AD and BQ |
Parallelograms on the same Base and between the same Parallels
Let us recall that “A diagonal of a parallelogram divides it into two triangles of equal area.” In case of a parallelogram, any side can be called its base, whereas the length of the line segment which is perpendicular to the base from the opposite side is called the altitude or height of the parallelogram corresponding to the given base.
In the figure,
- DP is the altitude of parallelogram ABCD, corresponding to the base AB.

- DQ is the altitude of parallelogram ABCD, corresponding to the base BC.
- BR is the altitude of parallelogram ABCD, corresponding to the base AD.
- CS is the altitude of parallelogram ABCD, corresponding to the base AB.
Theorem
Parallelograms on the same base (or on equal bases) and between the same parallels are equal in area.Proof
Let us have two parallelogram ABCD and ABEF on the same base AB and between the same parallel lines AB and FC.

In ΔADF and ΔBCE, AD = BC [Opposite sides of a parallelogram]
AF = BE [Opposite sides of a parallelogram]
∠DAF = ∠CBE [Since AD || BC and AF || BE]
∴ ΔADF ≌ ΔBCE [SAS criteria]

But congruent triangles are equal in area. ∴
ar (ΔADF) = ar (ΔBCE) Adding ar (ABED) to both sides, we have
ar (ΔADF) + ar (ABED) + ar (BCE) + ar (ABED)
⇒ ar (parallelogram ABEF) = ar (parallelogram ABCD).
Remember
- Area of a parallelogram is the product of its any side and the corresponding altitude.
- Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.
- Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels.
|
276 docs|149 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 9 - Exercise 9.1 Areas of Parallelograms and Triangles
| 1. What are the properties of parallelograms on the same base and between the same parallels? |  |
| 2. How can I find the area of parallelograms on the same base and between the same parallels? |  |
| 3. Can the area of parallelograms on the same base and between the same parallels be negative? |  |
| 4. What is the significance of parallelograms on the same base and between the same parallels? |  |
| 5. Can parallelograms on the same base and between the same parallels have different shapes? |  |

|
Explore Courses for Bank Exams exam
|

|

















