Expression Parsing | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Introduction
The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are:
- Infix Notation
- Prefix (Polish) Notation
- Postfix (Reverse-Polish) Notation
These notations are named as how they use operator in expression. We shall learn the same here in this chapter.
Infix Notation
We write expression in infix notation, e.g. a - b + c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption.
Prefix Notation
In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.
Postfix Notation
This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.
The following table briefly tries to show the difference in all three notations −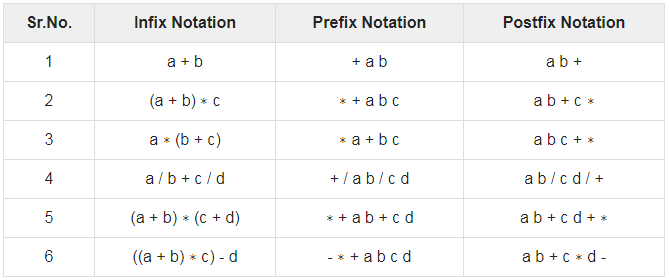
Parsing Expressions
As we have discussed, it is not a very efficient way to design an algorithm or program to parse infix notations. Instead, these infix notations are first converted into either postfix or prefix notations and then computed.
To parse any arithmetic expression, we need to take care of operator precedence and associativity also.
Precedence
When an operand is in between two different operators, which operator will take the operand first, is decided by the precedence of an operator over others. For example: As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later.
As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later.
Associativity
Associativity describes the rule where operators with the same precedence appear in an expression. For example, in expression a + b − c, both + and – have the same precedence, then which part of the expression will be evaluated first, is determined by associativity of those operators. Here, both + and − are left associative, so the expression will be evaluated as (a + b) − c.
Precedence and associativity determines the order of evaluation of an expression. Following is an operator precedence and associativity table (highest to lowest) −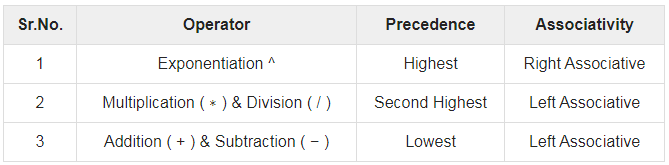
The above table shows the default behavior of operators. At any point of time in expression evaluation, the order can be altered by using parenthesis. For example −
In a + b*c, the expression part b*c will be evaluated first, with multiplication as precedence over addition. We here use parenthesis for a + b to be evaluated first, like (a + b)*c.
Postfix Evaluation Algorithm
We shall now look at the algorithm on how to evaluate postfix notation:
Step 1: scan the expression from left to right
Step 2: if it is an operand push it to stack
Step 3: if it is an operator pull operand from stack and perform operation
Step 4: store the output of step 3, back to stack
Step 5: scan the expression until all operands are consumed
Step 6: pop the stack and perform operation
|
158 docs|30 tests
|
FAQs on Expression Parsing - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is expression parsing? |  |
| 2. Why is expression parsing important? |  |
| 3. What are the different types of expressions that can be parsed? |  |
| 4. How is expression parsing typically implemented in programming languages? |  |
| 5. What are some challenges in expression parsing? |  |





















