Expression Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Introduction
The expression tree is a binary tree in which each internal node corresponds to the operator and each leaf node corresponds to the operand so for example expression tree for 3 + ((5+9)*2) would be: Inorder traversal of expression tree produces infix version of given postfix expression (same with postorder traversal it gives postfix expression)
Inorder traversal of expression tree produces infix version of given postfix expression (same with postorder traversal it gives postfix expression)
Evaluating the expression represented by an expression tree:
Construction of Expression Tree:
Now For constructing an expression tree we use a stack. We loop through input expression and do the following for every character.
- If a character is an operand push that into the stack
- If a character is an operator pop two values from the stack make them its child and push the current node again.
In the end, the only element of the stack will be the root of an expression tree.
Below is the implementation of the above approach:
- C++




- Java




- Python



- C#




- JavaScript



Output
infix expression is
a + b - e * f * g
Evaluation of Expression Tree
Given a simple expression tree, consisting of basic binary operators i.e., + , – ,* and / and some integers, evaluate the expression tree.
Examples:
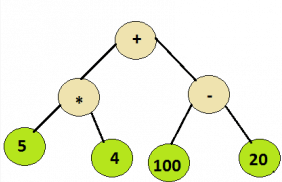
- Input:
Root node of the below tree
Output:
100 - Input:
Root node of the below tree Output:
Output:
110
As all the operators in the tree are binary hence each node will have either 0 or 2 children. As it can be inferred from the examples above , the integer values would appear at the leaf nodes , while the interior nodes represent the operators.
To evaluate the syntax tree , a recursive approach can be followed.
Algorithm

The time complexity would be O(n), as each node is visited once.
Below is a C++ program for the same:
- C/C++




- Python



Output:
- 60
- 110
|
119 docs|30 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|

















 Output:
Output:























