Factoring Polynomials | Preparation for EmSAT Grade 10 PDF Download
Factoring Polynomials means decomposing the given polynomial into a product of two or more polynomials using prime factorization. Factoring polynomials help in simplifying the polynomials easily. The first step is to write each term of the larger expression as a product of its factors. As a second step, the common factors across the terms are taken out in common to create the required factors. Let's discuss the methods of factoring polynomials, and some of the important concepts related to factoring polynomials: remainder theorem, factor theorem, GCF, long division.
What is Factoring of Polynomials?
The process of factoring polynomials involves expressing the polynomial as the product of its factors. Factoring polynomials help in finding the values of the variables of the given expression or to find the zeros of the polynomial expression. A polynomial is of the form axn + bxn - 1 + cxn - 2+ .........px + q, which can be factorized using numerous methods: grouping, using identities and substituting.
Here in this polynomial, the exponent of x is n and it has n factors. The number of factors is equal to the degree of the variable in the polynomial expression. Higher degree polynomials are reduced to a simpler lower degree, linear or quadratic expressions to obtain the required factors. Factoring polynomials can be understood with the help of a simple example. The quadratic polynomial x2 + x(a + b) + ab can be factorized as (x + a)(x + b).
Process of Factoring Polynomials
The following steps help for the process of factoring polynomials. Follow the below sequence of steps to factorize a polynomial.
- Factor out if there is a factor common to all the terms of the polynomial.
- Identify the appropriate method for factoring polynomials. You can use regrouping or algebraic identities to find the factors of the polynomial.
- Write polynomial as the product of its factors.
Methods of Factoring Polynomials
There are numerous methods of factoring polynomials, based on the expression. The method of factorization depends on the degree of the polynomial and the number of variables included in the expression. The four important methods of factoring polynomials are as follows.
- Method of Common Factors
- Grouping Method
- Factoring by splitting terms
- Factoring Using Algebraic Identities
Let us discuss each of the methods of factoring polynomials.
Method of Common Factors
This is the simplest method of factoring an algebraic expression by taking common factors of each of the terms of the given expression. As a first step, the factors of each of the terms of the algebraic expression are written. Further, the common factors across the terms are taken to obtain the possible factors. This is equivalent to using the distributive property in reverse. Let us understand this better with the help of an example.
Consider a simple example: 3x + 9
By factoring each term we get, 3 x + 3.3
By distributive law, 3x + 9 = 3.x + 3.3 = 3(x+3)
Factoring Polynomials By Grouping
The method of grouping for factoring polynomials is a further step to the method of finding common factors. Here we aim at finding groups from the common factors, to obtain the factors of the given polynomial expression. The number of terms of the polynomial expression is reduced to a lesser number of groups.
First, we split each term of the given expression into its factors and further aim at taking common terms to find the group of factors. Let us try to understand grouping for factorizing with the help of the following example. Let us solve an example problem to more clearly understand the process of factoring polynomials. Consider a polynomial: 8ab +8b + 28a + 28.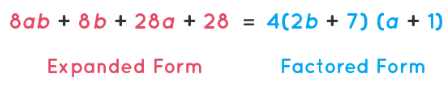
Notice that 4 is a single factor common to all the terms of this polynomial.
So, we can write 8ab+8b+28a+28 =4(2ab+2b+7a+7)
Let us group 2ab+2b and 7a+7 in the factor form separately.
2ab + 2b = 2b(a + 1), and 7a + 7 = 7(a + 1)
Now we have 8ab+8b+28a+28 = 4(2ab+2b+7a+7)
= 4 (2b(a + 1) + 7(a + 1))
= 4(2b + 7)(a + 1)
Thus the factoring polynomials is done by grouping. 8ab + 8b + 28a + 28 = 4(2b + 7)(a + 1)
Factoring Polynomials by Splitting Terms
The process of factoring polynomials is often used for quadratic equations. While factoring polynomials we often reduce the higher degree polynomial into a quadratic expression. Further, the quadratic equation has to be factorized to obtain the factors needed for the higher degree polynomial. The general form of a quadratic equation is x2 + x(a + b) + ab = 0, which can be split into two factors (x + a)(x + b) = 0. Consider the quadratic polynomial of the form x2 + x(a + b) + ab.
=x.x + ax + bx + ab
=x(x + a) + b(x + a)
=(x + a)(x + b)
Here in the above polynomial, the middle term is split as the sum of two factors, and the constant term is expressed as the product of these two factors. Thus the given quadratic polynomial is expressed as the product of two expressions. Let us understand this better, by factoring a quadratic polynomial x2 + 7x + 12.
x2 + 7x + 12
= x.x + 3x + 4x + 3.4
= x(x + 3) + 4(x + 3)
x2 + 7x + 12 = (x + 3)(x + 4)
Thus factoring polynomials is done using splitting the middle terms as in a quadratic polynomial.
Factoring Polynomials Using Algebraic Identities
The process of factoring polynomials can be easily performed using algebraic identities. The given polynomial expressions represent one of the algebraic identities. Also sometimes the given expression has to be modified so as to match with the expression of the algebraic identities. A few of the algebraic identities are helpful in factoring polynomials.
- a2 - b2 = (a + b)(a - b)
- a3 - b3 = (a - b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 - ab + b2)
- a4 - b4 = (a2 + b2)(a + b)(a - b)
Let's factorize the polynomial 4z2 - 12z + 9
Observe that 4z2 =(2z)2, 12z = 2 × 3 × 2z, and 9 = 32
So, we can write 4z2 - 12z+9 = (2x)2 + 2(2x)(3) + 32
= (2z - 3)2
Concepts Relating to Factoring Polynomials
The following concepts are helpful in factoring polynomials.
Remainder Theorem
The remainder theorem is helpful to find the remainder on dividing an algebraic expression with another expression, without actually performing the division. The remainder obtained when the algebraic expression f(x) is divided by ( x - a) is f(a). If f(a) = 0, then (x - a) is a factor of f(x). For a polynomial expression f(x) = 12x3 - 9x2 + 5x + 17, the remainder obtained on dividing it with (x - 2) is f(2) = 12(2)3 - 9(2)2 + 5(2) + 17 = 12(8) -9(4) + 10 + 17 = 96 - 36 + 27 = 87.
Factor Theorem
The factor theorem helps in connecting the factors and zeros of polynomials. If f(x) is a polynomial of degree n , a is a real number such that (x - a) is a factor of f(x), then f(a) = 0. Also if f(a) = 0 then (x - a) is a factor of f(x). The factor theorem is helpful to find if a given expression is a factor of a higher degree polynomial expression without actually performing the division.
Greatest Common Factors
The process of obtaining the greatest common factor for two or more terms includes two simple steps. First, split each of the terms into its prime factors, and then take as many common factors as possible from the given terms. Let us understand this by taking a simple expression of two terms 12x2 + 9x. Here we split the terms into its prime factors 12x2 + 9x = 2.2.3.x.x + 3.3.x. Among these two terms, we can take the maximum common terms to obtain the greatest common factors. Here we have the maximum common factor as 3x, and hence 12x2 + 9x = 2.2.3.x.x + 3.3.x = 3x(4x + 3).
Long Division
The process of long division involving polynomials is similar to the process of long division of natural numbers. Long division of polynomials is greatly helpful to find the factors of the given algebraic expression. The division resulting in a remainder of zero has the divisor as a factor of the polynomial expression. Divisions resulting in a remainder of zero can be written as Dividend = Divisor × Quotient. Thus the given polynomial expression gets divided into two factors. Further, the division of the below polynomial expression can be written as 4x2 - 5x - 21 = (x - 3)(4x + 7).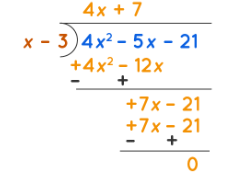
|
29 videos|254 docs|56 tests
|















