Factorization of Polynomials | Mathematics (Maths) Class 9 PDF Download
Factor theorem:
Let p(x) be a polynomial of degree n ≥ 1 and a be any real number such that,
(i) p(a) = 0, then (x − a) is a factor of p(x) conversely,
(ii)If (x − a) is a factor of p(x), then p(a) = 0
 Factor Theorem
Factor Theorem
Proof:
(i) Given p(a) = 0
Now, suppose p(x) is divided by (x − a), then quotient is g(x).
By remainder theorem, when p(x) is divided by (x − a), then remainder is p(a).
Dividend = Divisor × Quotient + Remainder
∴ p(x) = (x − a). g(x) + p(a)
p(x) = (x − a). g(x) + 0 [∵ p(a) = 0]
So, (x − a) is a factor of p(x)
(ii) Let (x − a) be a factor of p(x)
On dividing p(x) by (x − a), let g(x) be the quotient.
∴ p(x) = (x − a). g(x)
On putting x = a, we get
p(a) = (a − a). g(a)
p(a) = 0. g(a)
p(a) = 0
Thus, if (x − a) is a factor of p(x), then p(a) = 0
Examine whether x + 1 is a factor of p (x) = x3 + 3x3 + 5x + 6
Let p(x) = x3 + 3x2 + 5x + 6
By factor theorem, (x − a) is a factor of p(x) if p(a) = 0.
Therefore, in order to check that (x + 1) is a factor of p(x), it is sufficient to check that if p(−1) = 0 then it is a factor otherwise not.
p(x) = x3 + 3x2 + 5x + 6
p(– 1) = (– 1)3+ 3(– 1)2 + 5(– 1) + 6
p(– 1) = −1 + 3 − 5 + 6
p(– 1) = −6 + 9
p(– 1) = 3 ≠ 0
Thus, x + 1 is NOT a factor of p(x) = x3 + 3x2 + 5x + 6
Find the value of a if x-a is a factor of x3 - a2x + x + 2
Let p(x) = x3 − a2x + x + 2
By factor theorem, (x − a) is a factor of p(x) if p(a) = 0
Now, p(a) = a3 − a2 × a + a + 2
a3 − a2 × a + a + 2 = 0
a3 − a3 + a + 2 = 0
a + 2 = 0
a = 0 − 2
a = −2
Hence, (x − a) is a factor of the given polynomial, if a = −2
Factorisation of quadratic polynomial
Quadratic polynomial is represented as ax2 + bx + c, where a, b, c are constants and a ≠ 0. It can be factorised by different methods.
- By splitting the middle term
- By using factor theorem
(i) By splitting middle term
Let the factor of quadratic polynomial ax2 + bx + c be (px + q) and (rx + s). Then
ax2 + bx + c = (px + q)(rx + s)
= prx2 + (ps + qr)x + qs
Now,
Comparing x2, x and constant terms, we get
a = pr, b = ps + qr and c = qs
Here, b is the sum of two numbers ps and qr, whose product is (ps)(qr) = (pr)(qs) = ac
Thus, to factories ax2 + bx + c , write b as the sum of two numbers, whose product is ac.
Factorizing 2x2 + 7x + 3 by splitting the middle term
Given polynomial is 2x2 + 7x + 3 .
On comparing with ax2 + bx + c, we get
a = 2, b = 7 and c = 3
Now ac = 2 × 3 = 6
So, all possible pairs of factors 6 is 1 and 6, 2 and 3.
Pair 1 and 6 give 1 + 6 = 7 = b
∴ 2x2 + 7x + 3 = 2x2 + (1 + 6)x + 3
= 2x2 + x + 6x + 3
= x(2x + 1) + 3(2x + 1)
= (2x + 1)(x + 3)
(ii) By using factor theorem
Write the given polynomial p(x) = ax? + bx + c in the form
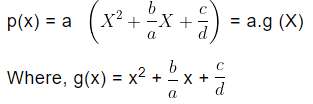
i.e. firstly make the coefficient of x2 equal to 1 if it is not 1.
Factories x2 - 5x + 6 by using factor theorem.
Let given polynomial be f(x) = x2 − 5x + 6
Here, the coefficient of x2 is 1, so we do not need to write it in the form of a. g(x).
Now, constant term is 6 and all factors of 6 are ±1, ±2, ±3 and ± 6
At x = 2,
f(2) = (2)2 − 5(2) + 6
f(2) = 4 − 10 + 6
f(2) = −6 + 6
f(2) = 0
At x = 3,
f(3) = (3)2 − 5(3) + 6
f(3) = 9 − 15 + 6
f(3) = −6 + 6
f(3) = 0
Hence, (x − 2) and (x − 3) are the factors of the given quadratic polynomial.
Factorisation of a cubic polynomial
We use the following steps to factorise a cubic polynomial,
Step I: Write the given cubic polynomial, p(x) = ax3+ bx2 + cx + d as,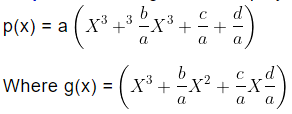
i.e., first make the coefficient of x= equal to 1 if it is not 1, then find the constant term.
Step II: Find all the possible factors of constant term (d/a) of g(X).
Step III: Check at which factor of constant term, p(x) is zero and get one factor of p(x), (i.e., x − α)
Step IV: Write p(x) as the product of this factor (x − α) and a quadratic polynomial i.e., p(x) = (x − α) (a1x2 + b1x + c1)
Step V: Apply splitting method of middle term or factor theorem in quadratic polynomial to get the other two factors. Thus, we get all the three factors of given the cubic polynomial.
Using factor theorem, factorise x3 + 13x2 + 32x + 20
Let p(x) = x3 + 13x2 + 32x + 20
Here the constant term = 20 and the coefficient of x3 is 1.
All possible factors of 20 are ±1, ±2, ±4, ±5, ±10, and ± 20
At x = −1,
p(x) = x3 + 13x2 + 32x + 20
p(−1) = (−1)3 + 13(−1)2 + 32(−1) + 20
= −1 + 13 − 32 + 20
= 33 − 33
= 0
So, we find p(−1) = 0 So, (x + 1) is a factor of p(x)
We can write the given polynomial x3+ 13x2 + 32x + 20 as, x3 + x2 + 12x2 + 12x + 20x + 20
x2+x2+12x2+12x+20x+20
= x2(x+1)+12x(x+1)+20(x+1)
= (x+1)(x2+12x+20) ........ (i) [Taking (x + 1) common]
Now, x2 + 12x + 20 can be factorised by splitting the middle term,
we get,
x2 + 12x + 20
= x2 + 10x + 2x + 20
= x(x + 10) + 2(x + 10)
= (x + 2)(x + 10) ...........(ii)
From equation (i) and (ii) we get,
x3+ 13x2+ 32x + 20 = (x + 1)(x + 2)(x + 10)
If p(y) = y3 −4y2 + y + 6 then show that p(3) = 0 and hence factorise p(y).
Given: p(y) = y3 − 4y2 + y + 6...... (i)
Put y = 3 in equation (i), we get
p(3) = (3)3 − 4(3)2 + 3 + 6
= 27 − 36 + 3 + 6 = 0
Since, p(3) = 0, therefore y – 3 is a factor of p(y).
∴ p(y) = (y − 3)(y2 − y − 2)
∴ p(y) = (y − 3)(y2 − 2y + y − 2)
[∵ −2 + 1 = −1 and − 2 × 1 = −2]
= (y − 3)[y(y − 2) + 1(y − 2])
= (y − 3)(y + 1)(y − 2)
|
44 videos|412 docs|54 tests
|
FAQs on Factorization of Polynomials - Mathematics (Maths) Class 9
| 1. What is the process of factorization of polynomials? |  |
| 2. How can I determine if a polynomial is factorizable? |  |
| 3. What are some common methods for factorizing polynomials? |  |
| 4. Can all polynomials be factorized completely? |  |
| 5. How can factorization of polynomials be useful? |  |

|
Explore Courses for Class 9 exam
|

|


















