Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Factorising Quadratics
Factorising Quadratics | Mathematics for GCSE/IGCSE - Class 10 PDF Download
| Table of contents |

|
| Factorising Simple Quadratics |

|
| Factorising Harder Quadratics |

|
| Difference of Two Squares |

|
| Quadratics Factorising Methods |

|
Factorising Simple Quadratics
What is a quadratic expression?
- A quadratic expression takes the form: ax2 + bx + c (where a ≠ 0).
- It ceases to be quadratic if it involves higher powers of x, such as x3.
- Monic vs. Non-Monic Quadratics:
- In the case where a = 1, it's termed a "monic" quadratic expression.
- For a ≠ 1, it's termed a "non-monic" quadratic expression.
How to Factorize Quadratics
Method 1: Factorizing "by inspection"
- This method involves finding a pair of numbers that multiply to a constant 'c' and add up to 'b'.
- For example, consider the quadratic expression: x2 - 2x - 8.
- To factorize, we need to find two numbers that multiply to -8 and add up to -2.
- These numbers are -4 and 2, which satisfy the conditions.
- Write these numbers in a pair of brackets, like this: (x - 4)(x + 2).
Method 2: Factorising "by grouping"
- This is best demonstrated with an example: factorizing x2 − 2x − 8.
- We need a pair of numbers that, for x2 + bx + c,
- multiply to c (in this case, -8)
- add to b (in this case, -2)
- The numbers 2 and -4 meet these conditions.
- Rewrite the middle term using 2x and −4x: x2 + 2x − 4x − 8
- Group and factorize the first two terms using 𝑥x as the common factor, and the second two terms using −4 as the common factor: x(x + 2) − 4(x + 2)
- Notice that both groups have a common factor of (x + 2), which can be factored out: (x + 2)(x − 4)
Method 3: Factorizing by Using a Grid
- This is best demonstrated with an example: factorizing x2 − 2x − 8.
- We need a pair of numbers that, for x2 + bx + c,
- multiply to c (which is -8)
- add to b (which is -2)
- The numbers -4 and +2 meet these conditions.
- Write the quadratic equation in a grid, splitting the middle term as −4x and 2x:
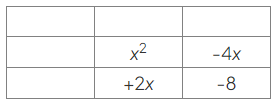
- Write a heading for the first row, using 𝑥x as the highest common factor of x2 and −4x:
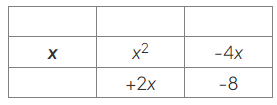
- Use this to find the headings for the columns, by asking "What does 𝑥x need to be multiplied by to give x2?":
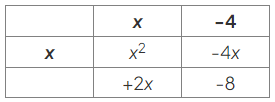
- Fill in the remaining row heading using the same idea, asking "What does 𝑥x need to be multiplied by to give 2x?":
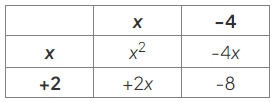
- Now, read off the factors from the column and row headings: (x + 2)(x − 4)
Which method should I use for factorising simple quadratics?
- The first method, by inspection, is the quickest and is recommended for simple quadratics (where a = 1) in an exam.
- However, the other two methods (grouping or using a grid) can be used for more difficult quadratic equations where a ≠ 1, so you should learn at least one of them as well.
Factorising Harder Quadratics
How to Factorise a Harder Quadratic Expression?
Factorising a ≠ 1 "by grouping"
- This is best demonstrated with an example: factorizing 4x2 − 25x − 21.
- We need a pair of numbers that, for ax2 + bx + c,
- multiply to ac (which is 4× − 21 = −84)
- add to b (which is -25)
- The numbers -28 and +3 meet these conditions.
- Rewrite the middle term using −28x and +3x:
4x2 − 28x + 3x − 21 - Group and factorize the first two terms using 4x as the highest common factor, and the second two terms using 3 as the factor:
4x(x − 7) + 3(x − 7) - Notice that these terms now have a common factor of (x − 7), so this whole bracket can be factored out, leaving 4x + 3 in its own bracket:
(x − 7)(4x + 3)
Factorising a ≠ 1 "by using a grid"
- This is best demonstrated with an example: factorizing 4x2 − 25x − 21.
- We need a pair of numbers that, for ax2 + bx + c,
- multiply to 𝑎𝑐ac (which in this case is 4× − 21 = −84)
- add to b (which in this case is -25)
- The numbers -28 and +3 meet these conditions.Write the quadratic equation in a grid, splitting the middle term as −28x and +3x:
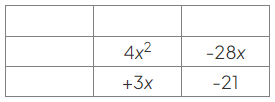
- Write a heading for the first row, using 4x as the highest common factor of 4x2 and −28x:
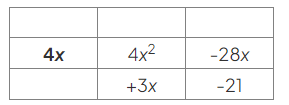
- Use this to find the headings for the columns, by asking "What does 4x need to be multiplied by to give 4x2?":
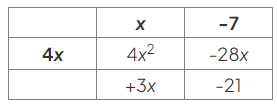
- Fill in the remaining row heading using the same idea, asking "What does x need to be multiplied by to give +3x?":
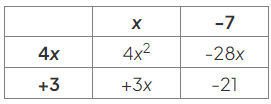
- Now, read off the factors from the column and row headings: (x − 7)(4x + 3)
Difference of Two Squares
- When a "squared" quantity is subtracted from another "squared" quantity, you get the difference of two squares.
- For example:
- a2 - b2
- 92 - 52
- (x + 1)2 - (x - 4)2
- 4m2 - 25n2, which is (2m)2 - (5n)2
How do I factorise the difference of two squares?
- Expand the brackets (a+b)(a−b):
- = a2 - ab + ba - b2
- Since ab is the same quantity as ba, −ab and +ba cancel out:
- = a2 - b2
- From the working above, the difference of two squares, a2 − b2, factorizes to:
(a + b)(a − b) - It is fine to write the second bracket first, (a − b)(a + b), but the a and the b cannot swap positions:
a2 − b2 must have the a’s first in the brackets and the b’s second in the brackets.
Quadratics Factorising Methods
How can we determine if a quadratic expression factorises?
- Method 1: Utilize a calculator to solve the quadratic expression set to 0. If the solutions are integers or fractions (without square roots), then the quadratic expression can be factorised.
- Method 2: Determine the value under the square root in the quadratic formula, b2 - 4ac (known as the discriminant). If this value is a perfect square number, then the quadratic expression factorises.
What factorization methods can be applied to quadratic expressions?
- Does it have 2 terms only?
- Yes, like x2 − 7x:
- Use "basic factorization" to take out the highest common factor:
x(x − 7)
- Use "basic factorization" to take out the highest common factor:
- Yes, like x2 − 9:
- Use the "difference of two squares" to factorize:
(x + 3)(x − 3)
- Use the "difference of two squares" to factorize:
- Yes, like x2 − 7x:
- Does it have 3 terms?
- Yes, starting with x2, like x2 − 3x − 10
- Use "factorizing simple quadratics" by finding two numbers that add to -3 and multiply to -10:
(x + 2)(x − 5)
- Use "factorizing simple quadratics" by finding two numbers that add to -3 and multiply to -10:
- Yes, starting with ax2, like 3x2 + 15x + 18
- Check if the 3 in front of x2 is a common factor for all three terms (which it is in this case), then use "basic factorization" to factor it out first:
3(x2 + 5x + 6) - The quadratic expression inside the brackets is now x2+…, which factorizes more easily:
3(x + 2)(x + 3)
- Check if the 3 in front of x2 is a common factor for all three terms (which it is in this case), then use "basic factorization" to factor it out first:
- Yes, starting with ax2, like 3x2 − 5x − 2
- The 3 in front of x2 is not a common factor for all three terms:
- Use "factorizing harder quadratics", such as factorizing by grouping or using a grid: (3x + 1)(x − 2)
- The 3 in front of x2 is not a common factor for all three terms:
- Yes, starting with x2, like x2 − 3x − 10
The document Factorising Quadratics | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|395 docs|19 tests
|
Related Searches



















