Factors and Common Factors | Year 5 Mathematics PDF Download
| Table of contents |

|
| Understanding Factors |

|
| Understanding Multiples |

|
| Understanding Common Factors |

|
| Understanding Prime Factors |

|
Understanding Factors
- Factors are numbers that divide into other numbers exactly, without any remainders.
- For instance, consider these eight ants. They can be grouped into one group of eight, or into two groups of four. Thus, the factors of eight are one, two, four, and eight. However, if you try to divide the eight ants into groups of three, you'll encounter problems, as eight doesn't divide evenly by three, leaving two ants without a group. So, three is not a factor of eight. It seems our hungry anteater wasn't expecting any leftovers.
How do we use factors?
- Factors are numbers that divide exactly into another number.
- For example, the factors of 8 are:
- 1, 2, 4, 8
- Factors can also be shown in pairs, with each pair multiplying to make 8.
- The factor pairs of 8 can be shown:
- 1 x 8 = 8
- 2 x 4 = 8
Understanding Multiples
Multiples of 2
- The multiples of 2 form the 2 times table, including numbers like 2, 4, 6, 8, 10, and so forth.
- All multiples of 2 end with: 2, 4, 6, 8, or 0.
- For instance, 2286 is a multiple of 2 because it ends with 6.

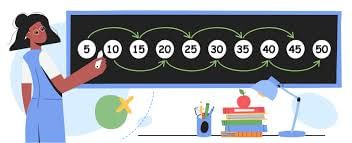
Multiples of 5
- Multiples of 5 are numbers that can be divided evenly by 5.
- They are part of the 5 times table, like 5, 10, 15, 20, 25, and so on.
- All multiples of 5 end with either 5 or 0.
- For instance, 465 is a multiple of 5 because it ends with 5.
Understanding Common Factors
- Definition of Factors: Factors are numbers that divide exactly into a given number. They represent the multiplication "facts" of that number.
- What are Common Factors: Common factors are those factors that are shared by two or more numbers.
- Example of Common Factor: For instance, the number 1 is a common factor for every single number because every number is divisible by 1.
Using an Ordered Method
To determine common factors without utilizing arrays, a systematic approach can be employed, known as an ordered method.
Examples
Example: 1
Let's consider an example scenario involving Bob the Baker who has prepared 9 doughnuts and 15 custard tarts and aims to distribute them equally into boxes. Each box can accommodate an equal number of doughnuts and custard tarts.
This problem necessitates identifying the common factor between 9 and 15.
Let's list down all factors of 9 and 15 and identify the factor they have in common:
Factors of 9: 1, 3, 9
Factors of 15: 1, 3, 5, 15 3 emerges as the common factor.
3 emerges as the common factor.
Thus, each box belonging to Bob the Baker can hold 3 doughnuts or 3 custard tarts.
Example: 2
Factors are numbers that can be multiplied together to get a specific number. Common factors are those that two or more numbers share.
Let's take an example to understand common factors: 16 and 48.
- Factors of 16: 1, 2, 4, 8, and 16.
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, and 16.
- Common factors of 16 and 48 are 1, 2, 4, 8, and 16.
Understanding Prime Factors
- A prime factor is a factor that is also a prime number, meaning it is divisible only by 1 and itself.
- Remember, 1 is not considered a prime number because it has only one factor.
- Prime factors play a crucial role in various mathematical concepts like prime factorization and finding the greatest common divisor.
Example: Common Prime Factors of 42 and 56
When finding the common prime factors between two numbers, such as 42 and 56, it's essential to first determine all factors of each number.
- Factors of 42: 1, 2, 3, 6, 7, 14, 21
- Factors of 56: 1, 2, 4, 7, 8, 14, 28
- By comparing the factors of 42 and 56, we can identify the common factors: 1, 2, 7, 14
However, not all common factors are prime numbers. Prime numbers are those that have only two factors: 1 and the number itself.
Prime Factors:
- 2 (as it has only factors 1 and 2)
- 7 (as it has only factors 1 and 7)
Therefore, the common prime factors of 42 and 56 are 2 and 7.
|
45 videos|42 docs|11 tests
|
FAQs on Factors and Common Factors - Year 5 Mathematics
| 1. What are factors and how do they relate to multiples? |  |
| 2. What are common factors and how are they determined? |  |
| 3. What are prime factors and how are they different from regular factors? |  |
| 4. How can understanding factors and multiples help in solving mathematical problems? |  |
| 5. How can students practice and improve their understanding of factors and multiples? |  |

|
Explore Courses for Year 5 exam
|

|
















