NCERT Solutions for Class 10 Maths Chapter 11 - Facts that Matter and Constructions (Exercise 11.1)
We know that:
- To divide a line segment in a given ratio m:n, we divide this segment into (m + n) equal parts. Then we take m parts on one side and n on the other.
- The idea of dividing a line segment in any ratio is used in the construction of a triangle similar to a given triangle, whose sides are in a given ratio with the corresponding sides of the given triangle.
- The scale factor means the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle.
Tangents to a Circle
Remember:
- If a point lies inside a circle, then there cannot be a tangent to the circle through this point.
- If a point lies on the circle, then there is only one tangent to the circle at this point and it is perpendicular to the radius through that point.
- If the point lies outside the circle, there will be two tangents to the circle from this point.
Note:
- For drawing a tangent at a point of a circle, simply draw the radius through this point and draw a line perpendicular to this radius through this point.
- The two tangents to a circle from an external point are equal.
Construction of Tangents to a Circle from a Point outside it.
Steps of construction:
- Let the centre of the circle be O and P be a point outside the circle.
- Join O and P.
- Bisect OP and let M be the midpoint of OP.
- Taking M as centre and MP or MO as radius, draw a circle intersecting the given circle at points A and B.
- Join PA and PB.
Thus, PA and PB are the required two tangents.
Note:
In case, the centre of the circle is not known, then to locate its centre, we take any two non-parallel chords and then find the point of intersection of their perpendicular bisectors.
Page No. 219 - 220
Exercise 11.1
In each of the following, give the justification of the construction also:
Q1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8.
Measure the two parts.
Ans: Steps of construction:
- Draw a line segment AB = 7.6 cm.
- Draw a ray AX making an acute angle with AB.
- Mark 13 (8 + 5) equal points on AX, and mark them as X1, X2, X3, ........, X13.
- Join ‘point X13’ and B.
- From ‘point X5’, draw X5C ║ X13B, which meets AB at C.
Thus, C divides AB in the ratio 5:8.
On measuring the two parts, we get: AC = 4.7 cm and BC = 2.9 cm.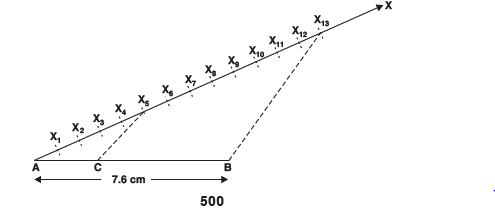
Justification:
In Δ ABX13 and Δ ACX5, we have
∴
⇒ AC : CB = 5 : 8.
Q2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Ans: Steps of construction:
- Draw a ∆ABC such that BC = 6 cm, AC = 5 cm and AB = 4 cm.
- Draw a ray BX making an acute angle ∠CBX.
- Mark three points X1, X2, X3 on BX such that BX1 = X1X2 = X2X3.
- Join X3C.
- Draw a line through X2 such that it is parallel to X3C and meets BC at C′.
- Draw a line through C′ parallel to CA to intersect BA at A′.
Thus, A′BC′ is the required triangle.Justification:
By construction, we have:
⇒ 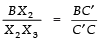
But 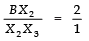
⇒ 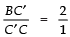
⇒ 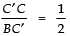
Adding, 1 to both sides, we get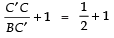
⇒ 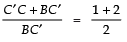
⇒
Now, in ΔBC′A′ and ΔBCA
we have CA ║ C′A′
∴ Using AA similarity, we have:
⇒ [each equal to 2/3]
Q3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle.
Ans: Steps of construction:
- Construct a Δ ABC such that AB = 5 cm, BC = 7 cm and AC = 6 cm.
- Draw a ray BX such that ∠CBX is an acute angle.
- Mark 7 points of X1, X2, X3, X4, X5, X6 and X7 on BX such that BX1 = X1X2 = X2X3 = X3X4 = X4X5 = X5X6 = X6X7
- Join X5 to C.
- Draw a line through X7 intersecting BC (produced) at C′ such that X5C ║ X7C′.
- Draw a line through C′ parallel to CA to intersect BA (produced) at A′. Thus, ΔA′BC′ is the required triangle.
Justification:
By construction, we have
C′A′ ║ CA
∴ Using AA similarity, ΔABC ~ ΔA′BC′
Also X7C′ ║ X5C [By construction
∴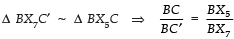
∴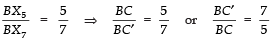
∴
Q4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are times the corresponding sides of the isosceles triangle.
Ans: Steps of construction:
- Draw BC = 8 cm
- Draw the perpendicular bisector of BC which intersects BC at D.
- Mark a point A on the above perpendicular such that DA = 4 cm.
- Join AB and AC.
Thus, ΔABC is the required isosceles triangle. - Now, draw a ray BX such that ∠CBX is an acute angle.
- On BX, mark three points X1, X2 and X3 such that: BX1 = X1X2 = X2X3
- Join X2 to C.
- Draw a line through X3 parallel to X2 C and intersecting BC (extended) to C′.
- Draw a line through C′ parallel to CA intersecting BA (extended) at A′, thus, ΔA′BC′ is the required triangle.
Justification:
We have C′A′ ║ CA [By construction]
∴ Using AA similarity, Δ ABC ~ ΔA′BC′
⇒
Since, X3C′ ║ X2C [By construction]
⇒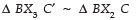
⇒ [By BPT]
[By BPT]
But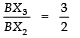
⇒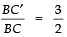
Thus,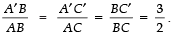
Q5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Ans: Steps of construction:
- Construct a ΔABC such that BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
- Draw a ray
such that ∠CBX is an acute angle.
- Mark four points X1, X2, X3 and X4 on BX such that BX1 = X1X2 = X2X3 = X3X4
- Join X4C and draw X3C′ ║ X4C such that C′ is on BC.
- Also, draw another line through C′ and parallel to CA to intersect BA at A′.
Thus, ΔA′BC′ is the required triangle.Justification:
By construction, we have:
X4C ║ X3C′ [By BPT]
But [By construction]
⇒ ...(1)
Now, we also have [By construction]
[using AA similarity]
⇒ [From (1)]
Q6. Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of Δ ABC.
Ans: Steps of construction:
- Construct a Δ ABC such that BC = 7 cm, ∠B = 45° and ∠A = 105°.
- Draw a ray BX making an acute angle ∠CBX with BC.
- On BX, mark four points X1, X2, X3 and X4 such that BX1 = X1X2 = X2X3 = X3X4.
- Join X3 to C.
- Draw X4C′ ║ X3C such that C′ lies on BC (extended).
- Draw a line through C′ parallel to CA intersecting the extended line segment BA at A′.
Thus, ΔA′BC′ is the required triangle.
Justification:
By construction, we have:
C′A′ ║ CA
∴ ΔABC ~ ΔA′BC′ [AA similarity]
⇒ ...(1)
Also, by construction,
X4C′ ║ X3C
Δ BX4C′ ~ Δ BX3C
⇒
But
⇒ ..(2)
From (1) and (2), we have:
Q7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Ans: Steps of construction:
- Construct the right triangle ABC such that ∠B = 90°, BC = 4 cm and BA = 3 cm.
- Draw a ray BX such that an acute angle ∠CBX is formed.
- Mark 5 points X1, X2, X3, X4 and X5 on BX such that BX1 = X1X2 = X2X3 = X3X4 = X4X5.
- Join X3 to C.
- Draw a line through X5 parallel to X3C, intersecting the extended line segment BC at C′.
- Draw another line through C′ parallel to CA intersecting the extended line segment BA at A′.
Thus, ΔA′BC′ is the required triangle.Justification:
By construction, we have:
C′A′ ║ CA
∴ ΔABC ~ Δ A′BC′ [By AA similarity ]
⇒ ...(1)
Also, X5C′ ║ X3C [By construction]
∴ Δ BX5C′ ~ Δ BX3C
⇒
But ...(2)
From (1) and (2) we get
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 11 - Facts that Matter and Constructions (Exercise 11.1)
| 1. What is a tangent to a circle? |  |
| 2. How many tangents can a circle have? |  |
| 3. What is the relationship between the radius of a circle and the tangent drawn to it? |  |
| 4. Can a tangent be drawn to the inside of a circle? |  |
| 5. How can we construct a tangent to a circle at a given point? |  |






















