Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Points to Remember: Triangles
Points to Remember: Triangles | Mathematics (Maths) Class 9 PDF Download
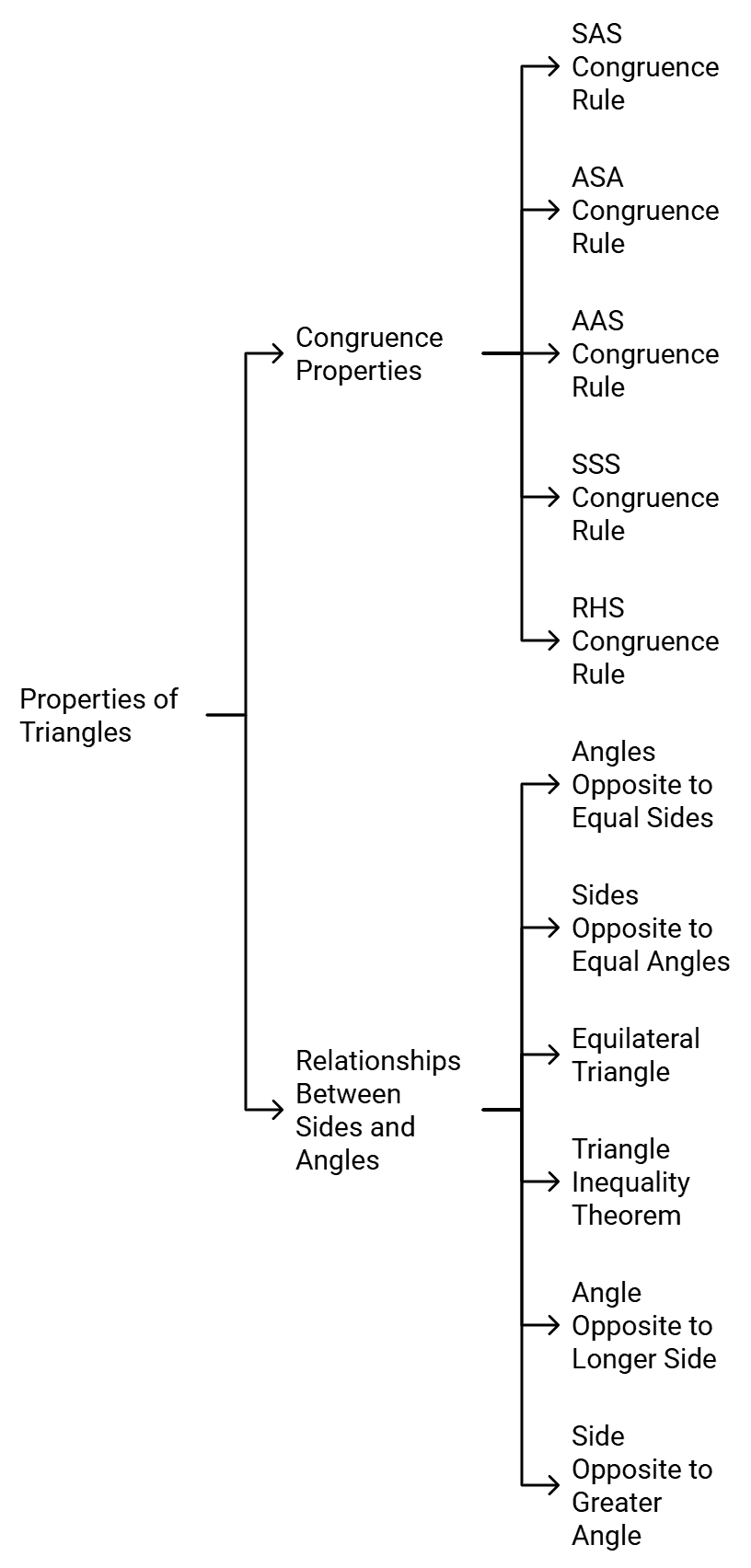
Properties of Triangles
Properties of Triangle
- Two congruent figures have exactly the same shape and size.
- If two triangles are congruent, then their corresponding parts are equal.
- If two sides and included angle of one triangle are equal to two sides and the included angle of the other triangle, then the two triangles are congruent. [SAS congruence rule]
- If two angles and the included side of one triangle are equal to two angles and included side of the other triangle, then the two triangles are congruent. [ASA congruence rule]
- If two angles and one side of a triangle are equal to two angles and the corresponding side of the other triangles, then the two triangles are congruent. [AAS congruence rule]
- If three sides of one triangle are equal to three sides of other triangle, then the two triangles are congruent. [SSS congruence rule]
- If in two right triangles, hypotenuse and one side of a triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. [RHS congruence rule]
- Angles opposite to equal sides of a triangle are equal.
- Sides opposite to equal angles are equal.
- The measure of each angle of an equilateral triangle is 60º.
- In a triangle, the sum of any two sides is always greater than the third side.
- In a triangle, the angle opposite to the longer side is (greater) larger.
- In a triangle, the side opposite to the greater angle is longer.
Congruent Figures
If two geometrical figures have exactly the same shape and size then they are called congruent figures.
Note: (i) Two line segments are congruent only when their lengths are equal.
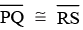
(ii) Two angles are congruent only when their degree measures are equal. ∠ABC ≌ ∠PQR
(iii) The symbol ‘≌’ is used to represent congruence.
Question for Points to Remember: TrianglesTry yourself: Which rule states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent?View Solution
Congruent Triangles
Two triangles are congruent if and only if one of them can be made to superimpose on the other, such as to cover it exactly.
In the figure, ΔABC ≌ ΔDEF.
Note: (i) When ΔABC ≌ ΔDEF, then sides of ΔDEF fall on corresponding equal sides of ΔABC, i.e.
DE covers AB or DE ↔ AB; EF covers BC or EF ↔ BC and FD covers CA or FD ↔ CA.
(ii) In case ΔABC ≌ ΔDEF,
∠D covers ∠A or ∠D ↔ ∠A.
∠E covers ∠B or ∠E ↔ ∠B.
∠F covers ∠C or ∠F ↔ ∠C.
(iii) In case ΔABC ≌ ΔDEF
D corresponds to A or D ↔ A.
E corresponds to B or E ↔ B.
F corresponds to C or F ↔ C.
(iv) In congruent triangles, corresponding parts are equal and we write in short ‘c.p.c.t.’ “for Corresponding Parts of Congruent Triangles”.
The document Points to Remember: Triangles | Mathematics (Maths) Class 9 is a part of the Class 9 Course Mathematics (Maths) Class 9.
All you need of Class 9 at this link: Class 9
|
44 videos|412 docs|54 tests
|
FAQs on Points to Remember: Triangles - Mathematics (Maths) Class 9
| 1. What are the properties of congruent triangles? |  |
Ans.Congruent triangles are triangles that are identical in shape and size, meaning their corresponding sides and angles are equal. The main properties include:
1. Corresponding sides of congruent triangles are equal in length.
2. Corresponding angles of congruent triangles are equal in measure.
3. If two triangles are congruent, any transformation (like rotation, reflection, or translation) applied to one will produce the other.
| 2. How can we prove that two triangles are congruent? | |
Ans.Two triangles can be proven congruent using several criteria:
1. Side-Side-Side (SSS) Criterion: If all three sides of one triangle are equal to the three sides of another triangle, they are congruent.
2. Side-Angle-Side (SAS) Criterion: If two sides and the included angle of one triangle are equal to those of another triangle, the triangles are congruent.
3. Angle-Side-Angle (ASA) Criterion: If two angles and the side between them in one triangle are equal to those in another triangle, the triangles are congruent.
4. Angle-Angle-Side (AAS) Criterion: If two angles and a non-included side of one triangle are equal to those in another triangle, they are congruent.
| 3. What is the significance of the congruence criteria in solving triangle problems? | |
Ans.The congruence criteria are significant in solving triangle problems as they provide a systematic approach to establishing the equality of triangles. They help in:
1. Determining unknown side lengths and angles in geometric problems.
2. Proving that certain triangles within a diagram are congruent, which simplifies the analysis of the figure.
3. Facilitating the use of congruent triangles in applications such as construction, design, and real-world problem-solving.
| 4. Can two triangles be congruent if they have the same angles but different side lengths? | |
Ans.No, two triangles cannot be congruent if they have the same angles but different side lengths. This scenario describes similar triangles, which have the same shape but not necessarily the same size. For triangles to be congruent, all corresponding sides must be equal in length, as well as all corresponding angles.
| 5. What are some real-life applications of congruent triangles? | |
Ans.Congruent triangles have various real-life applications, including:
1. Architecture and engineering, where congruent triangles are used in the design of stable structures.
2. Art and design, where congruent triangles help in creating balance and symmetry in visual compositions.
3. Navigation, where congruent triangles assist in triangulating positions and distances using landmarks.
Related Exams
About this Document
|
6.3K Views |
|
4.79/5 Rating |
|
Dec 23, 2024 Last updated |
Document Description: Points to Remember: Triangles for Class 9 2024 is part of Mathematics (Maths) Class 9 preparation.
The notes and questions for Points to Remember: Triangles have been prepared according to the Class 9 exam syllabus. Information about Points to Remember: Triangles covers topics
like Properties of Triangles, Congruent Figures and Points to Remember: Triangles Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Points to Remember: Triangles.
Introduction of Points to Remember: Triangles in English is available as part of our Mathematics (Maths) Class 9
for Class 9 & Points to Remember: Triangles in Hindi for Mathematics (Maths) Class 9 course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Points to Remember: Triangles | Mathematics (Maths) Class 9
Description
Full syllabus notes, lecture & questions for Points to Remember: Triangles | Mathematics (Maths) Class 9 - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 9 | Best notes, free PDF download
Information about Points to Remember: Triangles
In this doc you can find the meaning of Points to Remember: Triangles defined & explained in the simplest way possible. Besides explaining types of
Points to Remember: Triangles theory, EduRev gives you an ample number of questions to practice Points to Remember: Triangles tests, examples and also practice Class 9
tests
|
Explore Courses for Class 9 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Objective type Questions
,video lectures
,practice quizzes
,Points to Remember: Triangles | Mathematics (Maths) Class 9
,Summary
,Exam
,mock tests for examination
,Extra Questions
,Viva Questions
,Points to Remember: Triangles | Mathematics (Maths) Class 9
,Sample Paper
,study material
,shortcuts and tricks
,Previous Year Questions with Solutions
,Free
,MCQs
,ppt
,Semester Notes
,Important questions
,Points to Remember: Triangles | Mathematics (Maths) Class 9
,past year papers
;
Additional Information about Points to Remember: Triangles for Class 9 Preparation
Points to Remember: Triangles Free PDF Download
The Points to Remember: Triangles is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Points to Remember: Triangles now and kickstart your journey towards success in the Class 9 exam.
Importance of Points to Remember: Triangles
The importance of Points to Remember: Triangles cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Points to Remember: Triangles Notes
Points to Remember: Triangles Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Points to Remember: Triangles.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Points to Remember: Triangles Notes on EduRev are your ultimate resource for success.
Points to Remember: Triangles Class 9 Questions
The "Points to Remember: Triangles Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Points to Remember: Triangles on the App
Students of Class 9 can study Points to Remember: Triangles alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Points to Remember: Triangles,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Points to Remember: Triangles is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup