Finding Highest Normal Form | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Minimum relations satisfying First Normal Form (1NF)
The design of database proceeds in a following way:
- Talk to the stakeholder for which we are designing the database. Get all the requirements, what attributes need to be stored and establish functional dependencies over the given set of attributes.
- Draw an Entity-Relationship diagram on the basis of requirements analysis.
- Convert the ER-diagram into relational model and finally create these relations into our database with appropriate constraints.
We pretty much know, how to draw an ER-diagram. But, when we ask questions like how many minimum relations would be required satisfying first normal form (1NF), it is little confusing sometimes. We establish certain simple rules which are formed after deep analysis of each case and hence, could be used directly.
Note: It is not encouraged to mug up the rules, rather understanding the logic behind each case would help you remember them easily and for long time.
Algorithm
- If there is total participation on both sides;
- Merge the two entities involved and the relationship into 1 table.
- Else if, one side is total participation and one side is partial;
- M : N Merge the relationship on total participation side.
- 1 : N Merge the relationship on total participation side.
- 1 : 1 Merge the two entities involved and the relationship into 1 table.
- else if, both sides are partial participation;
- M : N Separate table for each entity as well as relationship. Hence, 3 tables.
- 1 : N Merge the relationship on N-side using foreign key referencing 1-side.
- 1 : 1 Merge the relationship and one entity into 1 table using foreign key and 1 table for other entity.
Now, you would definitely have a question in your mind, how we form such rules? This is very easy and logical. Let’s understand the logic behind it for one case and you can similarly establish the results for other cases too.
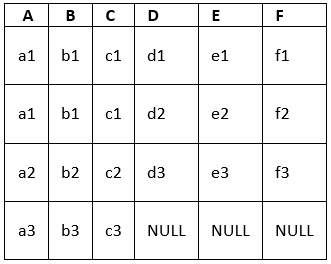
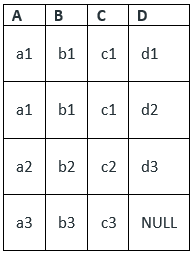
We have been given a scenario of 1 : N relationship with two entities E1(ABC) and E2(DEF), where A and D are primary keys, respectively. E1 has a partial participation while E2 has total participation in the relationship R.
Based on above scenario, we create certain tuples in E1:
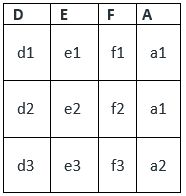
Similarly, create certain tuples for E2:
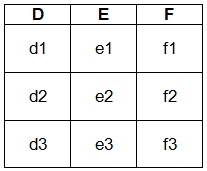
Now, create a relationship R satisfying above conditions, i.e. E1 is partial pariticipation and E2 is total participation and E1 to E2 is 1 : N relationship.
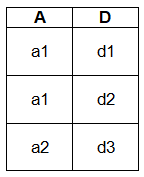
Think about possibilities, how can we merge?
- Way-1: Merge the two entities and relationship into a single table. This is not correct as (AD) will become primary key for this table, but primary key can never have a NULL value.

- Way-2: Merge relationship on 1-side. This is not correct as (AD) will become primary key for this table, but primary key can never have a NULL value.

- Way-3: Merge relationship on N-side. This is correct.

On the same grounds, could you think why we allow merging the two entities as well as relationship into 1 table, when it is a 1:1 relationship? Simply, we would not have a composite primary key there, so we will definitely have a primary key with no NULL values present in it. Stress some more, why we allow merging the entities and relationship with both sides total participation? The reason is even if we have a composite primary key for such merged table, we are sure that it will never have any NULL values for primary key.
Note: You can follow the same procedure as stated above to establish all the results.
How to find the highest normal form of a relation
Steps to find the highest normal form of a relation:
- Find all possible candidate keys of the relation.
- Divide all attributes into two categories: prime attributes and non-prime attributes.
- Check for 1st normal form then 2nd and so on. If it fails to satisfy nth normal form condition, highest normal form will be n-1.
Example 1: Find the highest normal form of a relation R(A, B, C, D, E) with FD set {A -> D, B -> A, BC -> D, AC -> BE}
Step 1: As we can see, (AC)+ = {A, C, B, E, D} but none of its subset can determine all attribute of relation, So AC will be candidate key. A can be derived from B, so we can replace A in AC by B. So BC will also be a candidate key. So there will be two candidate keys {AC, BC}.
Step 2: Prime attribute are those attribute which are part of candidate key {A,B,C} in this example and others will be non-prime {D,E} in this example.
Step 3: The relation R is in 1st normal form as a relational DBMS does not allow multi-valued or composite attribute.
The relation is not in 2nd Normal form because A->D is partial dependency (A which is subset of candidate key AC is determining non-prime attribute D) and 2nd normal form does not allow partial dependency.
So the highest normal form will be 1st Normal Form.
Example 2: Find the highest normal form of a relation R(A, B, C, D, E) with FD set as {BC -> D, AC -> BE, B -> E}
Step 1: As we can see, (AC)+ = {A, C, B, E, D} but none of its subset can determine all attribute of relation, So AC will be candidate key. A or C can’t be derived from any other attribute of the relation, so there will be only 1 candidate key {AC}.
Step 2: Prime attribute are those attribute which are part of candidate key {A, C} in this example and others will be non-prime {B, D, E} in this example.
Step 3: The relation R is in 1st normal form as a relational DBMS does not allow multi-valued or composite attribute.
The relation is in 2nd normal form because BC -> D is in 2nd normal form (BC is not proper subset of candidate key AC) and AC -> BE is in 2nd normal form (AC is candidate key) and B -> E is in 2nd normal form (B is not a proper subset of candidate key AC).
The relation is not in 3rd normal form because in BC->D (neither BC is a super key nor D is a prime attribute) and in B->E (neither B is a super key nor E is a prime attribute) but to satisfy 3rd normal for, either LHS of an FD should be super key or RHS should be prime attribute.
So the highest normal form of relation will be 2nd Normal form.
Example 3. Find the highest normal form of a relation R(A, B, C, D, E) with FD set {B -> A, A -> C, BC -> D, AC -> BE}
Step 1: As we can see, (B)+ ={B, A, C, D, E}, so B will be candidate key. B can be derived from AC using AC -> B (Decomposing AC -> BE to AC -> B and AC -> E). So AC will be super key but (C)+ = {C} and (A)+ ={A, C, B, E, D}. So A (subset of AC) will be candidate key. So there will be two candidate keys {A, B}.
Step 2: Prime attribute are those attribute which are part of candidate key {A, B} in this example and others will be non-prime {C, D, E} in this example.
Step 3: The relation R is in 1st normal form as a relational DBMS does not allow multi-valued or composite attribute.
The relation is in 2nd normal form because B -> A is in 2nd normal form (B is a super key) and A -> C is in 2nd normal form (A is super key) and BC -> D is in 2nd normal form (BC is a super key) and AC -> BE is in 2nd normal form (AC is a super key).
The relation is in 3rd normal form because LHS of all FD’s are super keys. The relation is in BCNF as all LHS of all FD’s are super keys. So the highest normal form is BCNF.
|
62 videos|66 docs|35 tests
|
FAQs on Finding Highest Normal Form - Database Management System (DBMS) - Computer Science Engineering (CSE)
| 1. What is the highest normal form in database design? |  |
| 2. How many normal forms are there in database design? |  |
| 3. What are the benefits of normalizing a database? |  |
| 4. What is the difference between 3NF and BCNF? |  |
| 5. How can I determine the normal form of a database? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|