Finding out Remainders | Quantitative for GMAT PDF Download
| Table of contents |

|
| What is Remainder? |

|
| Finding Remainders Using Long Division |

|
| How to Represent Remainder? |

|
| Basic Remainder Theorem |

|
| Concept of Negative Remainder |

|
Remainders is a very crucial concept since numerous questions from Quantitative Aptitude section require the concepts of remainder to solve them. Most of the candidates have already studied this concept in their elementary schools and can solve the related questions. Here is a lesson on Remainders to help the candidates revise the topic in an efficient way.
What is Remainder?
Suppose a number “N” is divided by another number “x”; if the quotient obtained is “Q” and the remainder obtained is “R”, then the number can be expressed as N = Qx + R.Example: Suppose 9 is divided by 2.
In this case, N = 9, x = 2, 2 × 4 = 8, which is 1 less than 9. hence Q = 4 and R = (9-8) = 1 . Hence, 9 = 4 × 2 + 1.
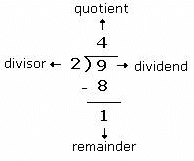
- In math, the number 17 cannot be exactly divided by the number 3. After division, the number 2 is left aside as a remainder.
- As an example, let us assume that you have 15 cookies that you want to share with 3 of your friends, Mary, David, and Jake. You want to share the cookies equally among your friends and yourself. You will be distributing them in the following way.

- Here, you can see that there are 3 cookies "remaining" after the distribution. These 3 cookies cannot be further shared equally among the 4 of you. Hence, 3 is called the "remainder". Also, on observation, the remaining 3 cookies are less in number than the 4 people, with whom the cookies have been shared. We can understand that the remainder is always lesser than the divisor.
Finding Remainders Using Long Division
We cannot always pictorially show how we divide the number of things equally among the groups in order to find the remainder. Instead, we can find the remainder using the long division method. For example, the remainder in the above example on cookies can be found using long division as follows: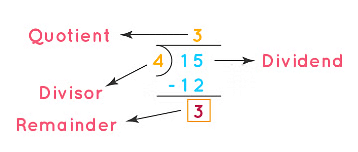
Thus, the remainder is 3. A remainder can also be a 0. The remainder on dividing 10 by 2, 18 by 3, or 35 by 7, is equal to 0. Here are some other examples of remainders.
| Division | Remainder |
| 35/6 | 5 |
| 42/8 | 2 |
| 121/11 | 0 |
| 118/12 | 10 |
| 120/17 | 1 |
How to Represent Remainder?
- Let us divide 7 by 2 using long division and see what the quotient and the remainder are. The quotient, divisor, the remainder can be together written as a mixed fraction to represent the dividend.
- The remainder forms the numerator of the mixed fraction, the divisor forms the denominator, and the quotient form the whole number part of the mixed fraction.
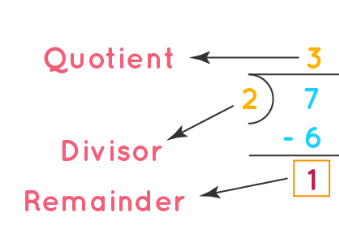
We can represent the remainder of the division in two ways.
- One is by writing the quotient and the remainder with an "R" in between them. The number 7 divided by 2 can be written as 7/2 = Q=3 and R=1. Here Q=3 is a quotient and R=1 is a remainder.
- Another way to represent the remainder is by showing it as a part of a mixed fraction. The number 7 divided by two can be written as 7/2 = 3½
Basic Remainder Theorem
The basic remainder theorem is based on the product of individual remainders. If R is the remainder of an expression( p*q*r)/X, and pR, qR and rR are the remainders when p,q and r are respectively divided by X, then it can be said that ((pR × qR × rR ))/X, will give the same remainder as given by (p*q*r)/X.
If R is the remainder of an expression( p*q*r)/X, and pR, qR and rR are the remainders when p,q and r are respectively divided by X, then it can be said that ((pR × qR × rR ))/X, will give the same remainder as given by (p*q*r)/X.
Let’s understand this with the help of some examples.
1. Find the remainder when (361*363) is divided by 12.
Steps:
- Take the product of individual remainders, i.e. 361/12|R =1 and 363/12|R = 3
- Find the remainder when you divide that product by the number (361 × 363)/12|R= (1 × 3)/12|R. answer= 3
This is Basic Remainder theorem put across in Numbers.
2. Find the remainder when 106 is divided by 7 i.e. (106/7)R.
Solution.
106=103 x 103
Thus (106/7)R = (103/7 × 103/7)R = ((6 * 6)/7)R = (36/7)R = 1.
So the remainder is 1.
“Remainder when the product of some numbers is divided by the requisite number is the product of individual remainders of the numbers”– This is Basic Remainder Theorem put across in words.
Concept of Negative Remainder
The remainder obtained by division of a number N by a divisor X can be expressed in two ways as “R” and “X - R”Example: 10/11 remainder is +10 itself. It can also be written as 10-11= -1 Similarly, 32/10 remainder is +2 or -8
Let’s express the solution for questions 31 above, in another way- based on the concept of negative remainder.
Thus (106/7)R = (103/7 × 103/7)R = ((-1 * -1)/7)R = (1/7)R = 1.
Let’s see why this happens:
If the numbers N1, N2, N3 give remainders of R1, R2, R3 with quotients Q1, Q2, Q3 when divided by a common divisor D.
N1 = DQ1 + R1 N2 = DQ2 + R2 N3 = DQ3 + R3
Multiplying = N1 × N2 × N3
= (DQ1 + R1) × (DQ2 + R2) × (DQ3 + R3)
= D(some number) + (R1 × R2 × R3) = first part is divisible by D,
Hence you need to check for the individual remainders only.
|
127 videos|154 docs|111 tests
|
FAQs on Finding out Remainders - Quantitative for GMAT
| 1. What is a remainder in mathematics? |  |
| 2. How can we find remainders using long division? |  |
| 3. What is the basic remainder theorem? |  |
| 4. How do we represent remainders in mathematics? |  |
| 5. Can remainders be negative? |  |
















