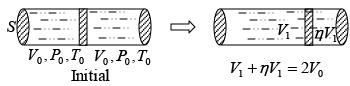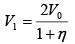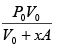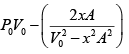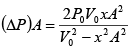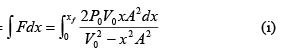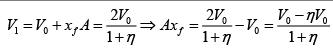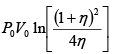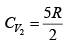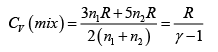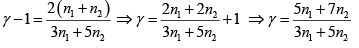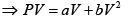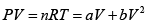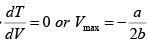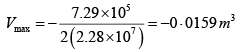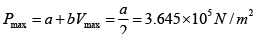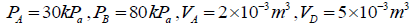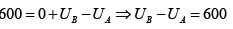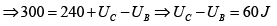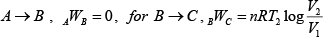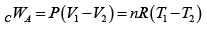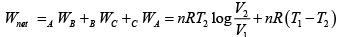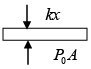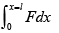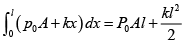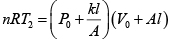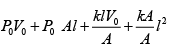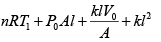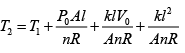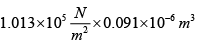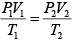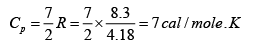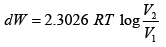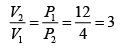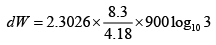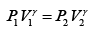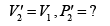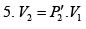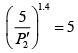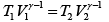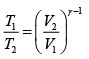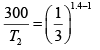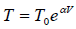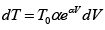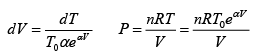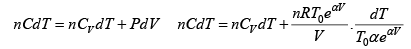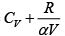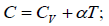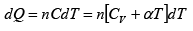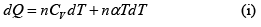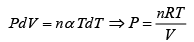First Law of Thermodynamics: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. A piston can freely move inside a horizontal cylinder closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts each of volume V in which an ideal gas is contained under the same pressure P0 and at the same temperature. What work has to be performed in order to increase isothermally the volume of one part of gas η times compared to that of the other by slowly moving the piston?
Suppose at time t , piston moves by x distance and in next dt time, piston moves
dx distance.
Since T = constant
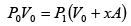
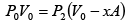
P1 =
P2 =
ΔP = P2 - P1 =
=
Force applied external agent:
F =
Work done W =
Here
put in (i) and integrate
W =
Q.2. Find the adiabatic exponent γ for a mixture consisting of n1 moles of a monatomic gas and n2 moles of gas of rigid diatomic molecules.
For monatomic gas
. For diatomic gas
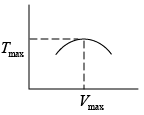
Q.3. Argon gas is contained in a cylinder. It goes to stats 2 from state 1. If the P-V
relationship is linear. The maximum temperature reached by the gas is
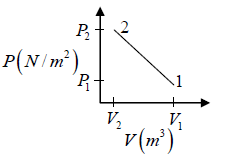
P1 = 4.1x105N /m2 ,V1 = 0.032m3
P2 = 15.5 x 105N/m2, V2 = 0.09m3
P = a+ bV
4.1x105 = a +b x 0 × 032
15.5 x105 = a +b x 0.09
b = 2.28 x107 N /m2, b = 7.29 x 105N/m2
As, P = a + bV
Or
Or
here k = nR (Constant)
Giving,
So,
= 685K (Put Value 2of R )
Q.4. 85 KJ heat is supplied to a system at constant volume. System rejects 90 KJ heat at constant pressure and 20 KJ of work is done on it. System is brought to original state by adiabatic process. Find adiabatic work and the internal energy at all the point. (U1 =100KJ).
1 → 2 , 1W2 = 0 , 1Q2 = 85 =U2 - U1
⇒U2 = 100 + 85 = 185 KJ
2 → 3, 2Q3 = U3 - U2 + 2W3
(2W3 = -20KJ) → -90 = U3 -185 + (-20)
⇒ U3= 115 KJ
Q = 0 (adiabatic process) ,
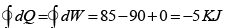
Since 1W2 +2W3 +3W1 = -5
3W1 = 15 KJ .
Q.5. In process AB,600KJ heat is added and in BC,300KJ heat is added. Find change in internal energy in AC .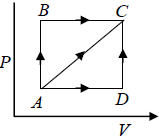
A →B , W =0 ⇒ AQB = AWB + UB - UA
= = 240 J
UC -UA = UC -UB +UB -UA = 60 + 600 = 660 J
Q.6. Calculate the heat absorbed by the system in going through the cyclic process.
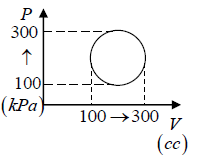
Work done by system = area under PV diagram = area of circle
⇒ W =
= 31.4 J
Q.7. For the circle ABCA (Fig), for an ideal gas find the net heat given to the system.

For cyclic process
For, C→A,
= constant (isobari – process)
And,
Q.8. 2 mol of monoatomic ideal gas (U =1.5nRT) is enclosed in an adiabatic vertical cylinder (Fig). Piston is adiabatic, spring has k = 200 N /m , piston cross – section area = 20cm2 . Initially spring is in natural length and T = 300k.Atm. pr is 100kPa . Gas is heated slowly so as to move the piston by 10cm .
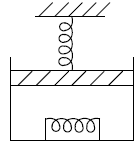
Find
(i) Work done by gas
(ii) Final temp
(iii) Heat Supplied by heater.
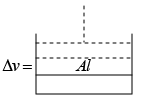
(i) Force by gas on piston F = P0A + kx , P0 = 100 kPa .
Work done by gas on piston W =
W =
W =
= 21J
(ii) For gas P0V0 = nRT , P2V2= nRT2
⇒
=
=
⇒
Putting nR =
and solving, T2 = 331K
(iii) As, ΔU = 1×5n RΔT
= 1.5 x 2 x 8.3 x 331 - 300) = 772 J
ΔQ = ΔW + ΔU = 772 + 21, = 793 J
Q.9. Calculate the change in internal energy when 0.004 kg of air is heated from 0oC to 2o C . The specific heat of air at constant volume being 0.172 kilo cal / kg oC .
From first law of thermodynamics
dQ = dU+ dW
where all quantities are measured in same units, say kilo cal.
Here air is heated at constant volume and hence no external work is done i.e .,
dW = p × dV = 0 .
Let m be the mass, cV the specific heat at constant volume and dT the rise in temperature of the air, the heat taken in by it is
dQ = m x CV x dT kilo cal .
Then from first law of thermodynamics
dU = dQ - dW = dQ
= m x C x dT = 0.004x 0.172 x2
= 1.376 x 10-3 kilo cal
Q.10. At normal temperature (0oC) and normal pressure (1.013x105 N /m2 , when 1 gm of water freezes, its volume increase by 0.091 cm3 . Calculate the change in internal energy. [Given: Latent heat of ice = 80 cal / gm ]
Heat given by 1 gm water when it freezes into ice
Q = mL = 1 gm x 80 cal / gm
= 80 cal = 80´ 4.2 Joule = 336 Joule
The external work done against the atmosphere when its volume increase by 0.0091 cm3 .
W = P.dV=
= 0.0093 Joule
By the first law of thermodynamics, the change in internal energy
ΔU = Q - W = (-336 - 0.0093) = =-336.0093 Joule
Here Q is taken negative because heat is given by the system. Thus internal energy decreases by 336.0093 Joule.
Q.11. When a system is taken from a state i to a state f , in fig., along the path iaf , we find dQ = 50 cals and W = 20 cals while along the path ibf ,dQ = 36 cals . If Ui = 10 cals .
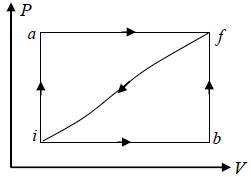
(i) What is Uf ?
(ii) What is W along the path ibf ?
(iii) If W = -13 cals along the curved path f i , what is dQ for this path?
(iv) If Ub = 22 cals what is dQ for the process ib ? For bf ?
Given that Ui = 10 cals , Q = 50 cals , W = 20 cals . For path iaf .
(i) From first law
Q = Uf - Ui +W
50 = Uf - 10 + 20
Uf = 50 +10 - 20 = 40 cals .
(ii) For the path ibf
Ui = 10 cals Uf = 40 cals
Q = 36 cals
W = Q - Uf + Ui = 36 - 40 +10 = 6 cals .
(iii) For the path fi
W =-13 cals
and dU = Ui -Uf = 10 - 40 = -30 cals
dQ = dU + dW = -30 - 13 = -43 cals
(iv) For the path bf
Uf = 40 cals Ub= 22 cals
dU = Uf -Ub = 40 - 22 = 18 cals
and, dQ = dU + dW = 18 + 0 = 18 cals
Because the work done ( dW = P. dV ) from b to f is zero as in the process volume remains constant.
And for the path ib
Ui = 10 cals Uf = 22 cals
dU = Ub - Ui = 22 -10 = 12 cals
And dW = 6 cals
∴ dQ = dU + dW = 12 + 6 = 18 cals
Q.12. A piston cylinder assembly contains 32 gm of oxygen at a pressure of 4 atmosphere and a temperature of 27oC . It undergoes a cycle in which it is first heated at constant volume until the pressure becomes three times, then it expand isothermally until the pressure drops to the original value and finally it is cooled isobarically back to the original temperature. Calculate the change in internal energy and the work done in each process.
Given atomic weight of oxygen =16 and R = 8.3 Joule /mole / K .
(i) When gas is heated at constant volume from 4.0 atoms to 12.00 atoms, the process is isochoric and since volume remains constant, the work done in the process
dW = P . dV=0
Hence from 1st law of thermodynamics
dQ = dU+ P . dV
= Cv dT+ 0
Now from

T2= 900K
Hence dT = 900- 300= 600 K
Also for a diatomic gas like oxygen
dQ = dU = CV dT = 5 x 600 = 3000 cals .
(ii) When the gas expands isothermally from 12 atmosphere to 4 atoms, the temperature remains constant and hence
dU = 0
Also for an isothermal process
Since, P1V1 = P2V2
= 1977 cals
(iii) When the gas is cooled isobarically (constant pressure)
dU = CVdT = 5 300 - 900)
=-3000 cals
Also dQ = CpdT = 7(300 900) = -4200 cals
dW = dQ- dU
= -4200 + 3000 = -1200 cals
=-1200 cals .
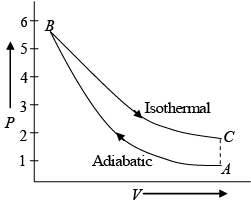
Q.13. A fixed mass of air at 1 atmosphere pressure is compressed adiabatically to 5
atmosphere and allowed to expand isothermally to its original volume.
(i) Represent these changes on a P-V diagram.
(ii) Calculate the pressure at the end of the isothermal process. Given γ for air =1.4 .
(i) The changes, the substance undergoes in the process of compression and expansion, are represented by a P -V curve shown in figure. Curve AB represents the adiabatic compression from 1 atoms to 5 atoms, while curve BC represents the isothermal expansion to its original volume. It is to be noted that the adiabatic curve is steeper than the isothermal curve.
(ii) During an adiabatic process
Here P1 = 1 atmosphere and P2 = 5 atmosphere
∴
Now during an isothermal process
As the gas expands from a pressure of 5 atmosphere and volume V2 to its original volume V1
P'1= 5 Atoms ., V'1= V2
Therefore, equation (ii) becomes
or
(iii)
Substituting, the value of
from (iii) into (i), we get
or
or pressure at the end of isothermal process
= 16 atmosphere.
Q.14. A quantity of air (γ =1.4) at 27oC is compressed (a) when the air is compressed slowly and (b) When the air is compressed suddenly to one third of its volume. Find the change in temperature in each case.
(a) when the air is compressed slowly, the heat generated conducts away to the surroundings. Thus it is an isothermal process temperature remains constant throughout, i.e. there is no change in temperature.
(b) When the air is compressed suddenly, the process is adiabatic.
Hence
= constant
If T1 ,V1 be the initial and T2 ,V2 the final temperature and volume respectively, then
or,
Here T1 = 27oC = (27 + 273) K = 300K,
γ =1.4.
Thus,
or, T2 = 300 (3)0.4 = 465.5 K = ( 465.5 - 273) = 192.5oC
Change in temperature T2 - T1 = 192.5 C - 27 C
= 165oC
Q.15. An ideal gas has a molar heat capacity Cv at constant volume. Find the molar heat capacity of this gas as a function of its volume V , if the gas undergoes the following process: 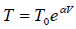
(a)
⇒
We know, dQ = dU + dW
Equating the coefficient of dT on both side C =
Q.16. For the case of an ideal gas find the equation of the process (in the variables T, V ) in which the molar heat capacity varies as: 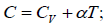
compare (i) and (ii)
|
6 videos|20 docs|32 tests
|
FAQs on First Law of Thermodynamics: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is the First Law of Thermodynamics? |  |
| 2. How does the First Law of Thermodynamics apply to the IIT JAM exam? |  |
| 3. Can you explain the First Law of Thermodynamics with an example? |  |
| 4. How is the First Law of Thermodynamics different from the Second Law of Thermodynamics? |  |
| 5. What are some real-life applications of the First Law of Thermodynamics? |  |