The classic example of a heat engine is a steam engine, although all modern engines follow the same principles. Steam engines operate in a cyclic fashion, with the piston moving up and down once for each cycle. Hot high-pressure steam is admitted to the cylinder in the first half of each cycle, and then it is allowed to escape again in the second half. The overall effect is to take heat Q1 generated by burning a fuel to make steam, convert part of it to do work, and exhaust the remaining heat Q2 to the environment at a lower temperature. The net heat energy absorbed is then Q = Q1 − Q2. Since the engine returns to its initial state, its internal energy U does not change (ΔU = 0). Thus, by the first law of thermodynamics, the work done for each complete cycle must be W = Q1 − Q2. In other words, the work done for each complete cycle is just the difference between the heat Q1 absorbed by the engine at a high temperature and the heat Q2 exhausted at a lower temperature. The power of thermodynamics is that this conclusion is completely independent of the detailed working mechanism of the engine. It relies only on the overall conservation of energy, with heat regarded as a form of energy.
In order to save money on fuel and avoid contaminating the environment with waste heat, engines are designed to maximize the conversion of absorbed heat Q1 into useful work and to minimize the waste heat Q2. The Carnot efficiency (η) of an engine is defined as the ratio W/Q1—i.e., the fraction of Q1 that is converted into work. Since W = Q1 − Q2, the efficiency also can be expressed in the form
 (2)
(2)
If there were no waste heat at all, then Q2 = 0 and η = 1, corresponding to 100 percent efficiency. While reducing friction in an engine decreases waste heat, it can never be eliminated; therefore, there is a limit on how small Q2 can be and thus on how large the efficiency can be. This limitation is a fundamental law of nature—in fact, the second law of thermodynamics.
Isothermal and adiabatic processes:
Because heat engines may go through a complex sequence of steps, a simplified model is often used to illustrate the principles of thermodynamics. In particular, consider a gas that expands and contracts within a cylinder with a movable piston under a prescribed set of conditions. There are two particularly important sets of conditions. One condition, known as an isothermal expansion, involves keeping the gas at a constant temperature. As the gas does work against the restraining force of the piston, it must absorb heat in order to conserve energy. Otherwise, it would cool as it expands (or conversely heat as it is compressed). This is an example of a process in which the heat absorbed is converted entirely into work with 100 percent efficiency. The process does not violate fundamental limitations on efficiency, however, because a single expansion by itself is not a cyclic process.
The second condition, known as an adiabatic expansion (from the Greek adiabatos, meaning “impassable”), is one in which the cylinder is assumed to be perfectly insulated so that no heat can flow into or out of the cylinder. In this case the gas cools as it expands, because, by the first law, the work done against the restraining force on the piston can only come from the internal energy of the gas. Thus, the change in the internal energy of the gas must be ΔU = −W, as manifested by a decrease in its temperature. The gas cools, even though there is no heat flow, because it is doing work at the expense of its own internal energy. The exact amount of cooling can be calculated from the heat capacity of the gas.
Many natural phenomena are effectively adiabatic because there is insufficient time for significant heat flow to occur. For example, when warm air rises in the atmosphere, it expands and cools as the pressure drops with altitude, but air is a good thermal insulator, and so there is no significant heat flow from the surrounding air. In this case the surrounding air plays the roles of both the insulated cylinder walls and the movable piston. The warm air does work against the pressure provided by the surrounding air as it expands, and so its temperature must drop. A more-detailed analysis of this adiabatic expansion explains most of the decrease of temperature with altitude, accounting for the familiar fact that it is colder at the top of a mountain than at its base.
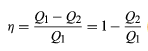 (2)
(2)























