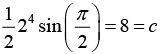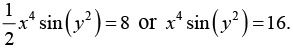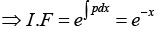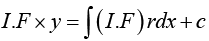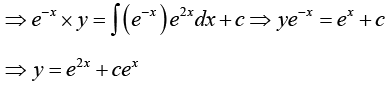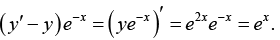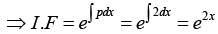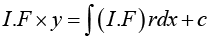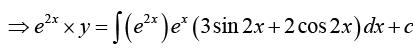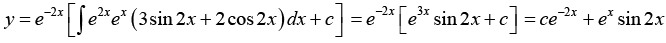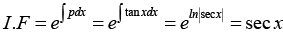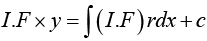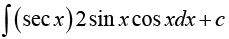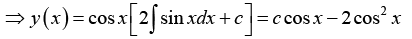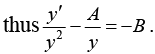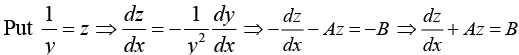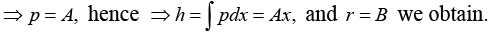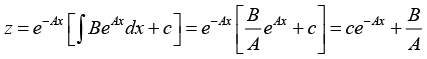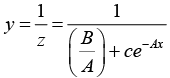First-Order Differential Equations | Mathematical Methods - Physics PDF Download
Concept of Order
The order of a differential equation is the order of the highest derivative that appears in the equation.
For example,
y' = cos x (First order differential equation),
y'' + 4y= 0 (Second order differential equation)
x2 y'''y' + 2y'' = x2 y2 (Third order differential equation)
The first-order differential equations contains only y' and may contain y and given functions of x . Hence we can write
F (x, y, y') = 0 or y' = f (x, y) ………(1)
Concept of Solution
A solution of a given first-order differential equation (1) on some open interval a < x< b is a function y =h (x) that has derivative y' = h' (x) and satisfies (1) for all x in that interval. Thus equation (1) becomes an identity if we replace the unknown function y by h (x) and y' by h' (x) .
Example: Verify that y = x 2 is a solution of xy' = 2y for all x .
Substitute y = x2 and y' = 2x into xy' = x x 2x = 2x2 = 2y , an identity in x .
Implicit Solution
Sometimes a solution of differential equation will appear as an implicit function, i.e.
H(x,y) = 0,
and is called an implicit solution, in contrast to an explicit solution y = h (x) .
Example: The function y of x implicitly given by x2+y2 - 1 = 0 (y > 0), represents a semicircle of unit radius in the upper-half plane. This function is an implicit solution of the differential equation yy' = -x on the interval -1< x < 1.
General and Particular Solution
Consider the differential equation y' = cos x .
Its solution will be y = sin x + c where c is an arbitrary constant. Such a function involving an arbitrary constant is called a general solution of a first order differential equation.
If we choose specific c(c = 2 or 0 or -5/3, etc), we obtain what is called a particular solution of that equation.
Thus y = sin x + c is a general solution of y' = cos x , and y = sin x , y = sin x - 2 , y = sinx + 0.75 , etc. are particular solutions.
Singular Solution
A differential equation may sometimes have an additional solution that can not be obtained from the general solution and is then called a singular solution.
For example, y'2 - xy' + y = 0 has the general solution y = cx- c2. Substitution also shows that the 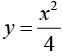 is also a solution. This is a singular solution because we cannot obtain it from y = cx- c2 by choosing a suitable c .
is also a solution. This is a singular solution because we cannot obtain it from y = cx- c2 by choosing a suitable c .
Initial Value Problems
A differential equation together with an initial condition is called an initial value problem. It is of the form
y' = f(x, y), y(x0) = y0
The initial condition y(x0) = y0 is used to determine a value of c in the general solution.
Separable Differential Equations
If a differential equation can be written in the form
f(y)dy = ∅(x)dx
We say that variables are separable, y on the left hand side and x on the right hand side. We get the solution by integrating both sides.
Example 1: Solve the differential equation 9 yy' + 4 x = 0 .
By separating variables we have
9 ydy =-4 xdx
Integrating both sides, we get
The solution represents a family of ellipses.
Example 2: Solve the differential equation y' = 1 + y2 .
By separating variables we have

Integrating both sides, we get
tan-1 y = x + c ⇒ y = tan (x + c)
Example 3: Solve the differential equation (yx2 + y) dy + (xy2 + x) dx = 0 .
Example 4: Solve the differential equation 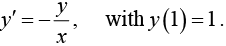
By separating variables we have
Integrating both sides, we get
Example 5: Solve the differential equation y' = -2 xy , with y (0) = 1.
By separating variables we have

Integrating both sides, we get
Settingwhen y > 0 , and
when y < 0 , and admitting also c = 0 (which gives the solution y = 0 ), we get the general solution
y = ce -x2
∵ y(0) = 1⇒ c = 1 ⇒ y ⇒ e -x2
Example 6: Solve the differential equation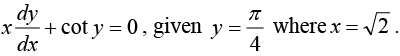
Homogeneous Equation (Reduction to Separable Form)
A differential equation of the form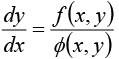
is called a homogeneous equation if each term of f (x, y) and ∅(x, y) is of the same degree.
Example 7: Find the solution of the differential equation 2 xyy' = y2 - x2 .
This general solution represents the family of circles with centers on the x -axis and all passing through origin.
Example 8: Find the solution of the differential equation 
Equations Reducible to Homogeneous Form
The equations of the form  can be reduced to homogeneous form by the substitutions x = X + h, y = Y + k ( h,k being constants)
can be reduced to homogeneous form by the substitutions x = X + h, y = Y + k ( h,k being constants)
Case of failure: 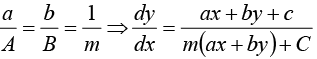
Now put ax + by = z and apply the method of separation of variables.
Example 9: 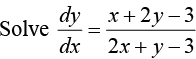
Put x = X + h, y = Y + k (h, k being constants)
The given equation reduces to
Now choose h, k so that
On integrating we havePut X = x - 1,Y = y - 1 ⇒ x+ y - 2 = a(x - y)3.
Example 10: 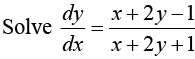
Put x + 2y = z ⇒
Exact Differential Equation
If a function u (x, y) has continuous partial derivatives, its differential is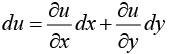
From this it follows that if u (x, y) = c = constant , then du = 0.
For example, if u = x + x2 y3 = c , then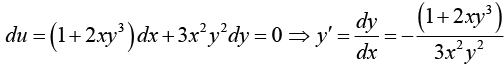
A differential equation that we can solve by going backward.
A first-order differential equation of the form
M (x, y) dx + N (x, y) dy = 0 …….(1)
is called an exact differential equation if differentia form M (x,y) dx + N(x,y) dy is exact, that is, this form is the differential
of some function u (x, y).
Then the differential equation (1) can be written
du = 0 .
By integrating we obtain general solution of (1) in the form
u (x, y) = c …….(3)
Comparing (1) and (2), we see that (1) is an exact differential if there is some function u (x, y) such that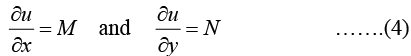
Thus 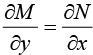
This condition is not only necessary but also sufficient for (1) to be an exact differential equation.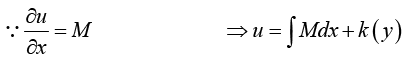
In this integration, y is to be regarded as a constant, and k (y) plays the role of a “constant” of integration. To determine k (y) , use 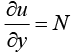 and find
and find 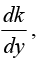 then integrate it to get k .
then integrate it to get k .
Similarly, 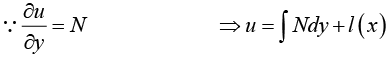
In this integration, x is to be regarded as a constant, and l (x) plays the role of a “constant” of integration. To determine 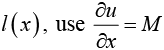 and find
and find 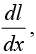 then integrate it to get k .
then integrate it to get k .
Example 11: Solve (x3 + 3xy2) dx + (3x2y + y3) dy = 0
1st Step
This is an exact differential equation.
2nd Step
Example 12: Solve (sin x cosh y) dx - (cos x sinh y)dy = 0 , y (0) = 3 .
1st Step
M = (sin x coshy) , N = (cos x sinh y) . Thus
This is an exact differential equation.
2nd Step
Thus u = - cosx cosh y + c' ⇒ u= cosx cosh y = c
∵ y (0) = 3 ⇒ cos 0 cosh 3 = 10.07 = c
⇒ cos x coshy = 10.07
Equations Reducible to the Exact Form
Consider the equation
- ydx + xdy = 0 .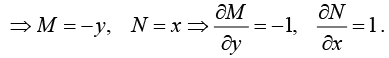
Hence equation is not exact. But if we multiply it by 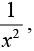 we get an exact equation,
we get an exact equation,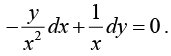
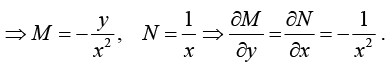
All we have done was the multiplication of a given nonexact equation, say
P (x, y) dx + Q (x, y) dy= 0
by a function F (x, y) . The result was an equation
FPdx + FQdy = 0
That is exact. The function F = F (x, y) is then called an integrating factor of
P (x, y) dx + Q (x, y) dy= 0
How to Find Integrating Factors
For FPdx + FQdy = 0 to be exact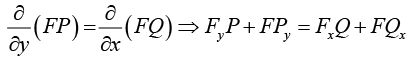
In the general case, this would be complicated and useless.
(a) For simplification let F = F (x) , Fy = 0, / Fx = F' = dF/dx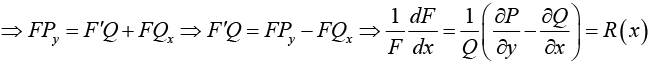
Integrating Factor F (x) = 
(b) If F = F (y), Fx = 0, Fy = F' = dF/dy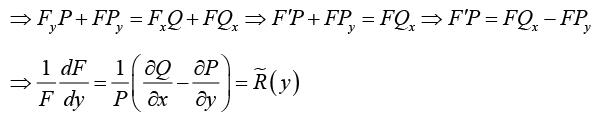
Integrating Factor 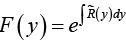
Example 13: Solve 2sin (y2) dx + xy cos (y2) = dy = 0, 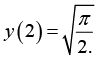
1st step: Check for exactness. We have
P = 2sin (y2) and Q = xy cos (y2)
The equation is not exact because
Py = 4ycos (y2) ≠ Qx = y cos (y2)
2nd step: Integrating factor
Thus the integrating factor is
Multiplying the given equation by x3, we get
2x3sin (y2) dx + x4 y cos(y2) dy = 0
This equation is exact because
3rd Step: General Solution
Hence k ' (y) = 0 and k = const. this give the general solution
4th step: Particular solution
Substituting the initial conditioninto u (x, y), we have
Hence the desired particular solution is
Linear Differential Equations
A first-order differential equation is said to be linear if it can be written as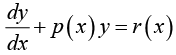
where p and r are function of x (but not y) or constant.
If r(x) = 0 , the equation is said to be homogeneous; i.e.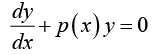
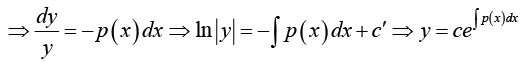
If r (x) ≠ 0 , the equation is said to be nonhomogeneous; i.e.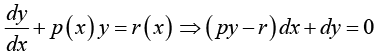
Compare with Pdx + Qdy = 0 , thus P = (py - r), Q = 1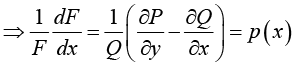
Integrating Factor F (x) = 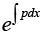
Multiplying 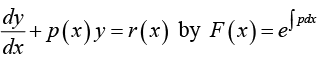
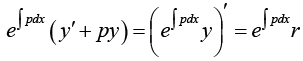
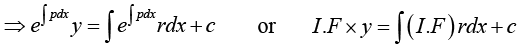
Example 14: Solve the linear differential equation y' - y = e2x .
Here p = -1, r = e2x ,
Thus general solution
In simpler cases, such as the present, we may not need the general formula but may wish to proceed directly; multiplying the given equation by eh = e-x . This gives
Example 15: Solve y' + 2y = ex (3sin 2x + 2 cos 2 x)
Here p = 2, r = ex (3 sin 2 x + 2 cos 2 x)
Thus general solution
Example 16: Solve the initial value problem
y' + y tan x = sin 2x , y (0) = 1
Here p = tan x,r = sin 2 x = 2 sin x cos x and
The general solution is
⇒ sec x x y =
From this and the initial condition 1 = c - 1- 2.12 ; thus c = 3 and the solution of our initial value problem is y = 3cosx- 2 cos2 x.
Equation Reducible to Linear Form
A differential equation of the form 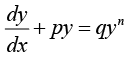
where p and q are function of x (but not y) or constant can be reduced to the linear form on dividing by yn and substituting 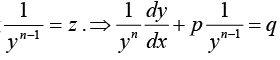
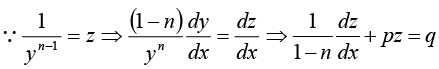
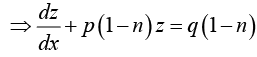 which is a linear differential equation.
which is a linear differential equation.
Example 17: Solve y' - Ay= - By2
Divide above equation by y2,
This gives the general solution
|
78 videos|18 docs|24 tests
|
FAQs on First-Order Differential Equations - Mathematical Methods - Physics
| 1. What is the concept of order in first-order differential equations? |  |
| 2. What is the concept of a solution in first-order differential equations? |  |
| 3. What is the IIT JAM exam? |  |
| 4. What are some frequently asked questions in the IIT JAM exam related to the concept of first-order differential equations? |  |
| 5. Can you provide some tips for preparing for the IIT JAM exam and mastering the concept of first-order differential equations? |  |

|
Explore Courses for Physics exam
|

|
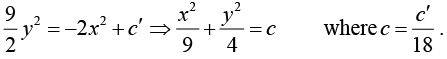
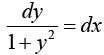
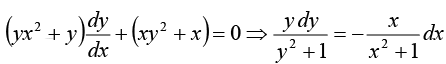
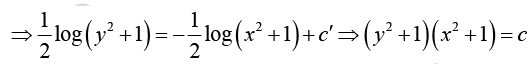
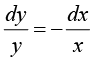
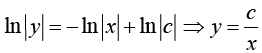
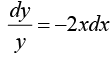
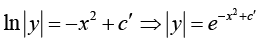
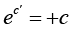 when y > 0 , and
when y > 0 , and 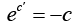 when y < 0 , and admitting also c = 0 (which gives the solution y = 0 ), we get the general solution
when y < 0 , and admitting also c = 0 (which gives the solution y = 0 ), we get the general solution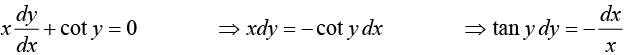
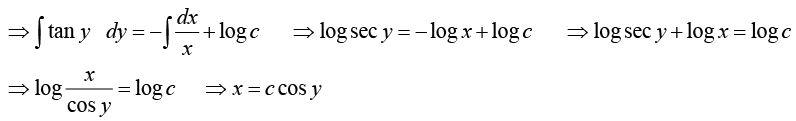
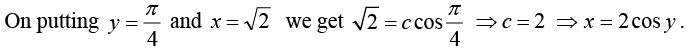
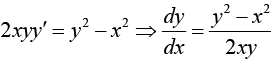
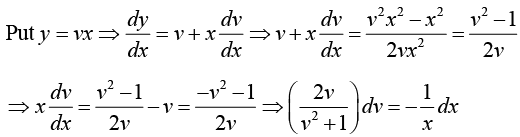
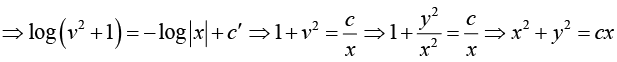
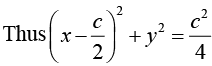
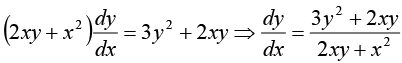
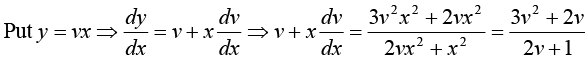
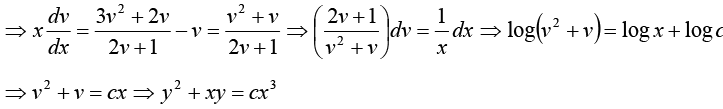
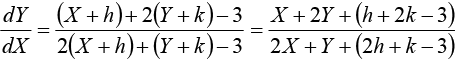
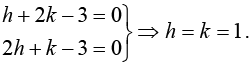
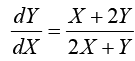
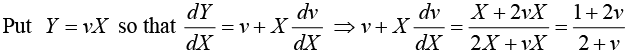
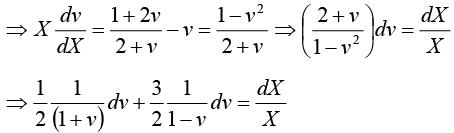
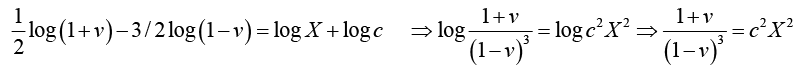
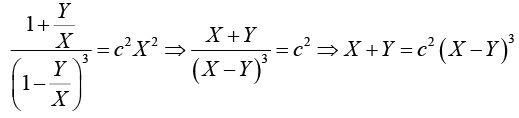
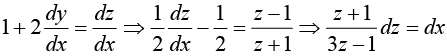
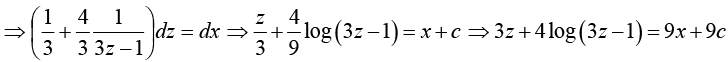
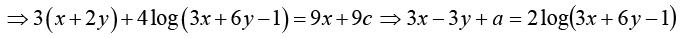
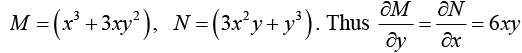
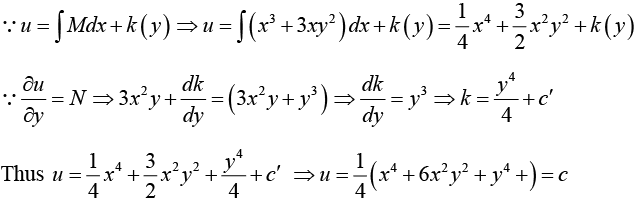
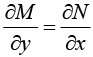
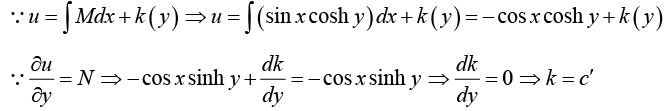
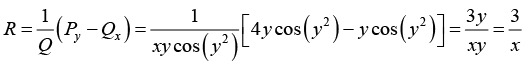
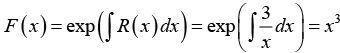
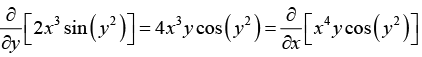
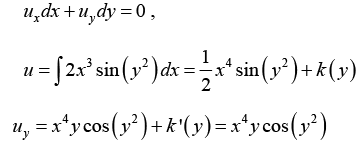
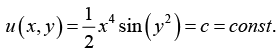
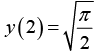 into u (x, y), we have
into u (x, y), we have