|
Flashcards: Area and Volume 36 Flashcards 
|
|
|
Card: 1 / 36 
|
What is the formula for the area of a rectangle? |
|
|
Card: 2 / 36
|
The area of a rectangle is calculated using the formula A = length × width. For example, if a rectangle has a length of 5 units and a width of 3 units, its area is A = 5 × 3 = 15 square units.  |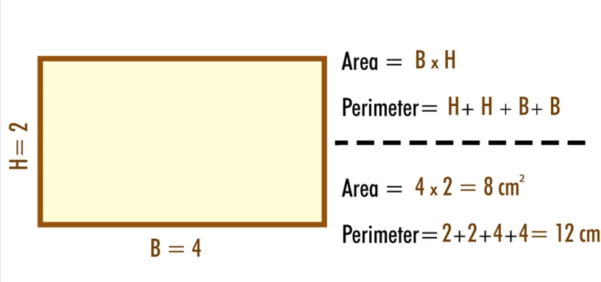
|
|
Card: 3 / 36
|
How do you calculate the volume of a rectangular prism? |
|
|
Card: 4 / 36
|
The volume of a rectangular prism is calculated using the formula V = length × width × height. For example, if the dimensions of the prism are 4 units long, 3 units wide, and 2 units high, the volume is V = 4 × 3 × 2 = 24 cubic units. |
|
|
Card: 5 / 36
|
What is the formula for the area of a triangle? |
|
|
Card: 6 / 36
|
The area of a triangle is calculated using the formula A = 1/2 × base × height. For example, if a triangle has a base of 6 units and a height of 4 units, its area is A = 1/2 × 6 × 4 = 12 square units. |
|
|
Card: 7 / 36
|
If the radius of a circle is 3 units, what is its area? Hint: Use the formula A = πr². |
|
|
Card: 8 / 36
|
To find the area, use the formula A = πr². Substituting the radius: A = π(3)² = π × 9 = 9π square units. (Approximately 28.27 square units if π is approximated as 3.14.) |
|
|
Card: 9 / 36
|
How do you find the volume of a cylinder with a radius of 2 units and a height of 5 units? Hint: Use the formula V = πr²h. |
|
|
Card: 10 / 36
|
To calculate the volume, use the formula V = πr²h. Substituting the values: V = π(2)²(5) = π × 4 × 5 = 20π cubic units. (Approximately 62.83 cubic units if π is approximated as 3.14.) |
|
|
Card: 11 / 36
|
What is the formula for the total surface area of a cube? Hint: Consider the number of faces and their dimensions. |
|
|
Card: 12 / 36
|
The total surface area of a cube is calculated using the formula TSA = 6l², where l is the length of one side. For example, if the side length is 4 units, TSA = 6(4)² = 96 square units. |
|
|
Card: 13 / 36
|
How do you calculate the volume of a cone with a radius of 3 cm and a height of 4 cm? Hint: Use the formula V = 1/3 πr²h. |
|
|
Card: 14 / 36
|
To find the volume, use V = 1/3 πr²h. Substituting the values: V = 1/3 π(3)²(4) = 1/3 π(9)(4) = 12π cubic cm. (Approximately 37.68 cubic cm if π is approximated as 3.14.) |
|
|
Card: 15 / 36
|
What is the formula for the lateral surface area of a cylinder? Hint: Consider the curved surface. |
|
|
Card: 16 / 36
|
The lateral surface area of a cylinder is given by LSA = 2πrh, where r is the radius and h is the height. For example, if r = 2 cm and h = 5 cm, then LSA = 2π(2)(5) = 20π square cm. |
|
|
Card: 17 / 36
|
If a cube has a side length of 2 m, what is its volume? Hint: Use the formula V = l³. |
|
|
Card: 18 / 36
|
The volume of a cube is calculated using V = l³. Therefore, V = (2)³ = 8 cubic meters. |
|
|
Card: 19 / 36
|
What is the relationship between the radius and height of a cone when finding its volume? Hint: The formula involves both radius and height. |
|
|
Card: 20 / 36
|
The volume of a cone is given by V = 1/3 πr²h, which shows that both the radius (r) and height (h) are crucial for calculating volume. |
|
|
Card: 21 / 36
|
How do you find the volume of a sphere with a radius of 3 units? Hint: Use the formula V = 4/3 πr³. |
|
|
Card: 22 / 36
|
The volume of a sphere is calculated using V = 4/3 πr³. Substituting the radius: V = 4/3 π(3)³ = 36π cubic units. (Approximately 113.10 cubic units if π is approximated as 3.14.) |
|
|
Card: 23 / 36
|
What is the total surface area of a hemisphere with a radius of 5 units? Hint: Combine the curved surface area and base area. |
|
|
Card: 24 / 36
|
The total surface area of a hemisphere is TSA = 3πr². Therefore, for r = 5, TSA = 3π(5)² = 75π square units. |
|
|
Card: 25 / 36
|
If a rectangular prism has a length of 8 cm, width of 3 cm, and height of 2 cm, what is its volume? Hint: Use the formula V = lwh. |
|
|
Card: 26 / 36
|
The volume is V = lwh = 8 × 3 × 2 = 48 cubic cm. |
|
|
Card: 27 / 36
|
What is the formula for the volume of a pyramid? Hint: Consider the base area and height. |
|
|
Card: 28 / 36
|
The volume of a pyramid is given by V = 1/3Bh, where B is the area of the base and h is the height. |
|
|
Card: 29 / 36
|
How do you calculate the diagonal length of a cube with side length 4 units? Hint: Use the formula d = √3l. |
|
|
Card: 30 / 36
|
The diagonal length of a cube is calculated using d = √3l. Therefore, for l = 4, d = √3(4) = 4√3 units. |
|
|
Card: 31 / 36
|
What is the formula for the surface area of a sphere? Hint: It involves the radius. |
|
|
Card: 32 / 36
|
The surface area of a sphere is given by SA = 4πr². For example, if r = 3, SA = 4π(3)² = 36π square units. |
|
|
Card: 33 / 36
|
If a cylinder has a height of 10 cm and a base radius of 3 cm, what is its volume? Hint: Use the formula V = πr²h. |
|
|
Card: 34 / 36
|
The volume is V = π(3)²(10) = 90π cubic cm. (Approximately 282.74 cubic cm if π is approximated as 3.14.) |
|
|
Card: 35 / 36
|
What is the formula for the area of a trapezoid? Hint: It involves the lengths of the bases and the height. |
|
|
Card: 36 / 36
|
The area of a trapezoid is given by A = 1/2(b₁ + b₂)h, where b₁ and b₂ are the lengths of the two bases and h is the height. |
|
|
|
 Completed! Keep practicing to master all of them. |
|
