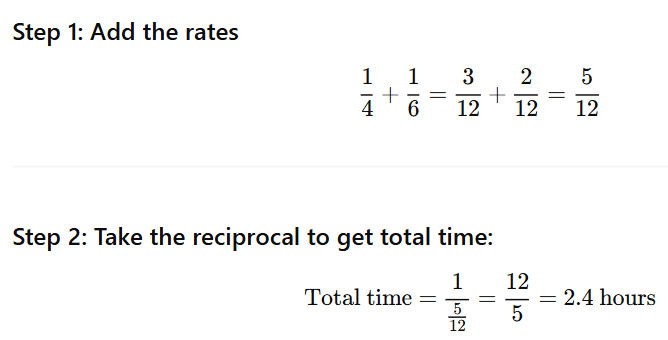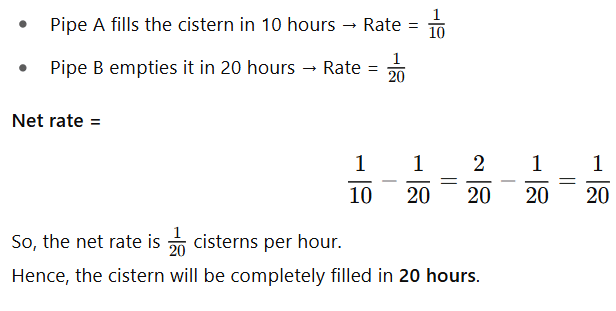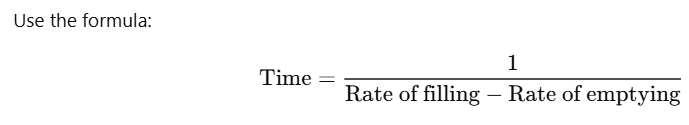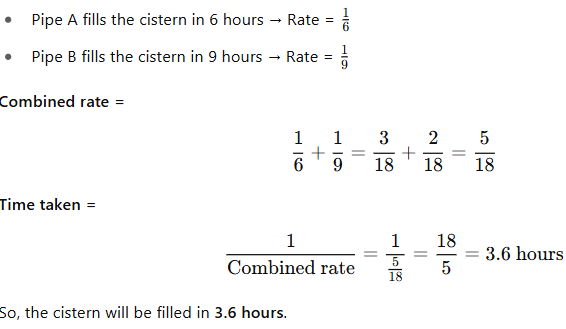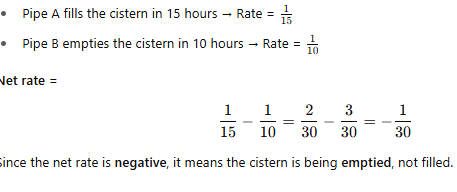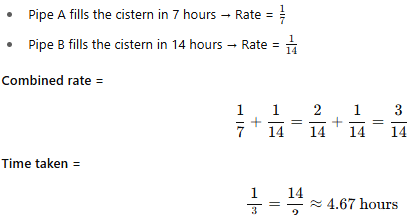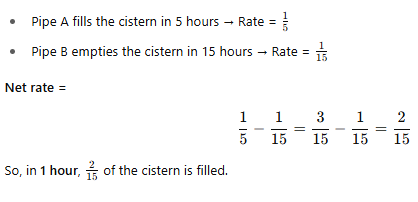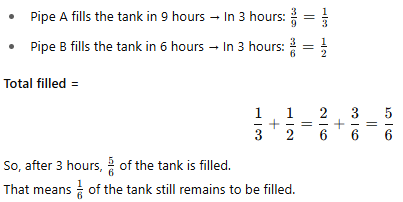|
What is the formula to calculate the time taken to fill a cistern using multiple pipes? |
Card: 1 / 28 |
|
The formula to find the total time taken to fill a cistern using multiple pipes is: |
Card: 2 / 28 |
|
If Pipe A can fill a cistern in 4 hours and Pipe B can fill it in 6 hours, how long will it take for both pipes to fill the cistern together? |
Card: 3 / 28 |
|
A cistern is filled by Pipe A in 8 hours and emptied by Pipe B in 12 hours. What is the net rate when both pipes are open? |
Card: 5 / 28 |
|
If a cistern can be filled by Pipe A in 10 hours and emptied by Pipe B in 20 hours, how long will it take to fill the cistern with both pipes open? |
Card: 7 / 28 |
|
How do you calculate the time taken to fill a cistern if one pipe is filling it and another is emptying it? |
Card: 9 / 28 |
|
A cistern is filled by Pipe A in 5 hours and Pipe B fills it in 3 hours. If both pipes are opened for 1 hour, how much of the cistern is filled? |
Card: 11 / 28 |
|
If Pipe A can fill a cistern in 6 hours and Pipe B in 9 hours, how long will it take both pipes to fill the cistern if they work together? |
Card: 13 / 28 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
A cistern is being filled by two pipes, A and B, which can fill it in 4 hours and 6 hours, respectively. If both pipes are opened for 2 hours, how much of the cistern is filled? |
Card: 15 / 28 |
|
If Pipe A can fill a cistern in 8 hours and Pipe B can empty it in 10 hours, how long will it take to fill the cistern with both pipes open? |
Card: 17 / 28 |
|
A cistern can be filled by Pipe A in 15 hours and emptied by Pipe B in 10 hours. What is the net rate if both are open? |
Card: 19 / 28 |
|
If Pipe A fills a cistern in 7 hours and Pipe B fills it in 14 hours, how long will they take together? |
Card: 21 / 28 |
|
A cistern is filled by Pipe A in 5 hours and emptied by Pipe B in 15 hours. If both are open, how much of the cistern is filled in 1 hour? |
Card: 23 / 28 |
|
If Pipe A can fill a tank in 9 hours and Pipe B can fill it in 6 hours, how long will it take to fill the tank if both pipes are opened for 3 hours? |
Card: 25 / 28 |
|
A cistern can be filled by Pipe A in 12 hours and emptied by Pipe B in 18 hours. How long will it take to fill the cistern with both pipes open? |
Card: 27 / 28 |





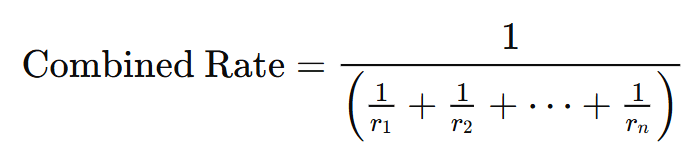 where r₁, r₂, ..., rₙ are the rates of each pipe.
where r₁, r₂, ..., rₙ are the rates of each pipe.