|
Magic patterns are arrangements of numbers where the sum of each row, column, and diagonal equals the same value; a common example is a magic square. 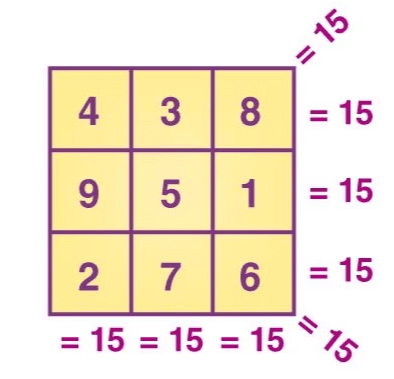 |
Card: 4 / 34 |
|
True or False: The sum of the numbers in a magic square can vary between different rows. |
Card: 5 / 34 |
|
Fill in the blank: By identifying underlying rules in patterns, students apply pattern recognition to ___ scenarios. |
Card: 7 / 34 |
|
Riddle: I am an arrangement where every row, column, and diagonal sum to the same value. What am I? |
Card: 9 / 34 |
|
A magic triangle is a triangular arrangement of numbers where the sums of each row and the sums along the diagonals are equal, similar to magic squares which have the same property in a square arrangement. |
Card: 12 / 34 |
|
True or False: In a magic tower, every cube contains a number that can be duplicated across different levels. |
Card: 13 / 34 |
|
How do magic triangles and magic towers enhance understanding of mathematical concepts? |
Card: 15 / 34 |
|
They provide insights into symmetry and number theory, encouraging spatial reasoning and problem-solving skills.  |
Card: 16 / 34 |
|
Magic triangles are arranged in ___ shape, while magic squares are arranged in ___ shape. |
Card: 17 / 34 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
The 'same sum rule' ensures that the sum of numbers in every row, column, and diagonal of a magic square remains ___. |
Card: 19 / 34 |
|
True or False: Patterns with addition can be used to predict future terms in a sequence. |
Card: 21 / 34 |
|
It refers to a situation where something is inverted or reversed from its usual orientation, such as flipping a shape or text vertically. |
Card: 30 / 34 |
|
Fill in the blank: A floor pattern is created by arranging materials like tiles or wood on the ___. |
Card: 31 / 34 |
|
False. Floor patterns are commonly used in interior design to enhance aesthetics. |
Card: 34 / 34 |