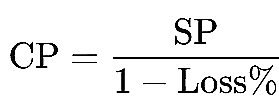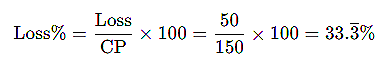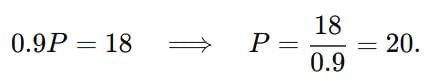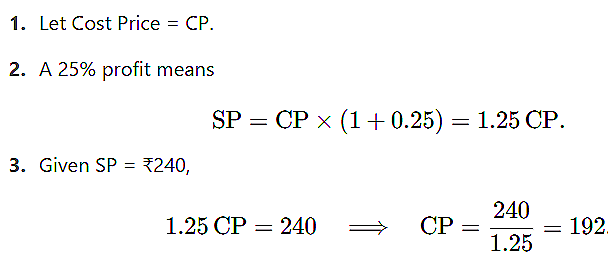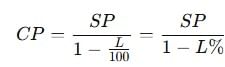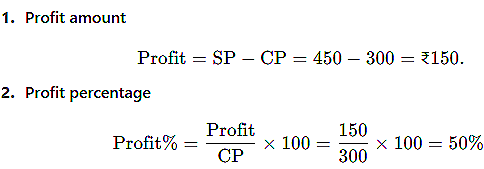|
Cost price (CP) is the amount paid to acquire a product or service. |
Card: 2 / 28 |
|
Profit is calculated using the formula: |
Card: 4 / 28 |
|
Loss percentage is calculated using the formula: |
Card: 6 / 28 |
|
If a person sells a watch for ₹240 and incurs a loss of 20%, what is the cost price of the watch? |
Card: 7 / 28 |
|
If the selling price is ₹240 and this represents 80% of the cost price, = 240 / 0.80 = 300 |
Card: 8 / 28 |
|
Calculate the selling price if an item is bought for ₹300 and a profit of 15% is desired. |
Card: 9 / 28 |
|
Selling Price is calculated as: SP = CP + Profit. |
Card: 10 / 28 |
|
Profit is the financial gain achieved when the revenue from sales exceeds the total costs incurred in producing and selling a product or service. It is calculated using the formula: |
Card: 12 / 28 |
|
If an item is purchased for ₹150 and sold for ₹100, What is the loss and the loss percentage? |
Card: 13 / 28 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
A book is sold for ₹18 after a discount of 10%. What was the original price of the book? |
Card: 15 / 28 |
|
Let the original price be x. The selling price after a 10% discount is x - 0.10x = 0.90x. |
Card: 16 / 28 |
|
If a seller experiences a profit of 25% on an item sold for ₹240, what was the cost price? |
Card: 17 / 28 |
|
If a retailer buys a product for ₹400 and wants to achieve a profit of 30%, what should be the selling price? |
Card: 19 / 28 |
|
First calculate the profit: Profit = 30% of Cost Price = 0.30 x ₹400 = ₹120. |
Card: 20 / 28 |
|
A store offers a discount of 15% on a pair of shoes originally priced at ₹80. What is the selling price after the discount? |
Card: 21 / 28 |
|
The discount is calculated as 15% of ₹80, which is ₹12. |
Card: 22 / 28 |
|
The break-even point is the point at which total revenue equals total costs, resulting in neither profit nor loss. |
Card: 24 / 28 |
|
If a company sells a product for ₹500 and incurs a 20% loss, what is the cost price of the product? |
Card: 25 / 28 |
|
If the selling price is ₹500 and this represents 80% of the cost price (since a 20% loss means the selling price is 80% of the cost), |
Card: 26 / 28 |
|
Calculate the profit percentage if a product is bought for ₹300 and sold for ₹450. |
Card: 27 / 28 |





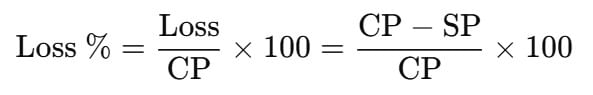 If a product with a CP of 200 is sold for 150,
If a product with a CP of 200 is sold for 150,