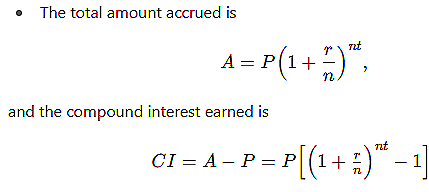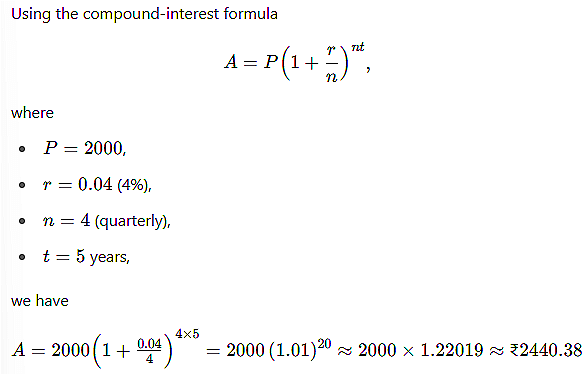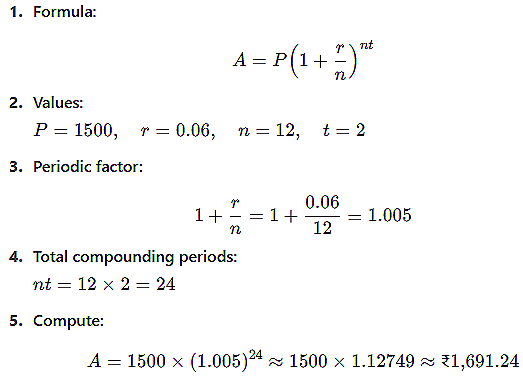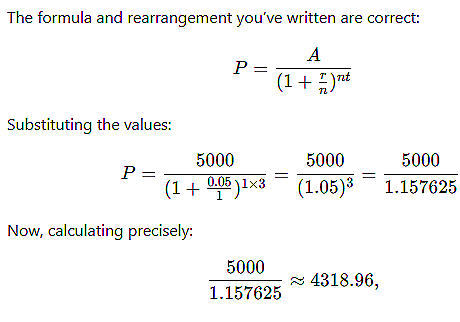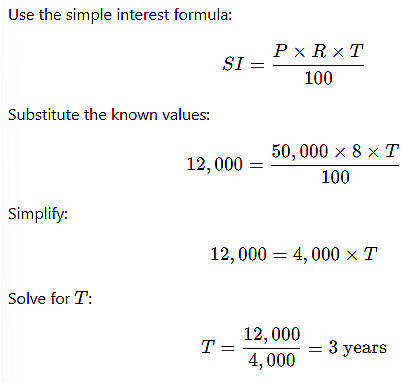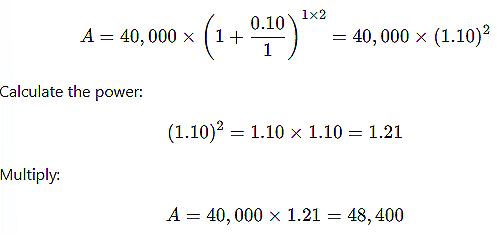|
The formula for calculating Simple Interest (SI) is |
Card: 2 / 20 |
|
If you invest ₹1,000 at an annual interest rate of 5% for 3 years, How much total interest will you earn? |
Card: 3 / 20 |
|
Simple Interest is calculated only on the principal amount, whereas Compound Interest is calculated on the principal plus any interest that has been added to it over time. This means that with Compound Interest, you earn interest on your interest. |
Card: 6 / 20 |
|
If you invest ₹2,000 at an annual interest rate of 4% compounded quarterly for 5 years, what will be the total amount at the end of the investment? |
Card: 9 / 20 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
What is the effective annual rate (EAR) when interest is compounded quarterly at a nominal rate of 8%? |
Card: 11 / 20 |
|
You deposit ₹1,500 into a savings account that earns 6% interest compounded monthly. How much will you have in the account after 2 years? |
Card: 13 / 20 |
|
If you want to accumulate ₹5,000 in 3 years with an account that pays 5% annual compound interest, what principal amount do you need to invest today? |
Card: 15 / 20 |
|
A sum of ₹50,000 is lent out at a simple interest rate of 8% per annum. After how many years will the interest earned be ₹12,000? |
Card: 17 / 20 |
|
An amount of ₹40,000 is invested at a compound interest rate of 10% per annum, compounded annually. What will be the total amount after 2 years? |
Card: 19 / 20 |





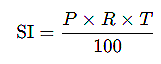 ,
,