|
The relationship is defined by the formula: Distance = Speed × Time. |
Card: 2 / 20 |
|
The formula for calculating speed is |
Card: 4 / 20 |
|
If a runner covers a distance of 10 km in 50 minutes, what is their speed in km/h? |
Card: 5 / 20 |
|
First, convert 50 minutes to hours: |
Card: 6 / 20 |
|
A car travels 120 km in 1.5 hours. How long will it take to travel an additional 180 km at the same speed? |
Card: 7 / 20 |
|
Two trains leave the same station at the same time. Train A travels at 70 km/h and Train B at 90 km/h. How far apart will they be after 2 hours? |
Card: 9 / 20 |
|
Distance of Train A |
Card: 10 / 20 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
If a cyclist and a motorist travel the same distance of 100 km, and the cyclist's speed is 15 km/h while the motorist's speed is 60 km/h, who arrives first and by how much time? |
Card: 11 / 20 |
|
Time for cyclist |
Card: 12 / 20 |
|
A boat travels upstream at 10 km/h and downstream at 15 km/h. What is the average speed of the boat for a round trip of 30 km upstream and 30 km downstream? |
Card: 13 / 20 |
|
Total distance = 30 km upstream + 30 km downstream |
Card: 14 / 20 |
|
A train travels 240 km at a speed of 60 km/h. How long does the journey take?
|
Card: 15 / 20 |
|
Using the formula: |
Card: 16 / 20 |
|
If a cyclist travels at a speed of 15 km/h and takes a break for 30 minutes after riding for 1.5 hours, what distance does he cover before the break? |
Card: 17 / 20 |
|
Distance = Speed × Time = 15 km/h × 1.5 h |
Card: 18 / 20 |
|
A car travels from City A to City B, a distance of 300 km, at an average speed of 75 km/h. If the car stops for 1 hour, what is the total time for the journey? |
Card: 19 / 20 |
|
Travel time without the stop = Distance / Speed = 300 km / 75 km/h = 4 hours. Total time = 4 hours + 1 hour (stop) = 5 hours. |
Card: 20 / 20 |





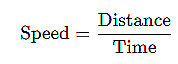
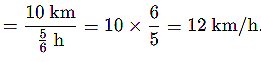 .
.















