Floating-Point Number Representation | Digital Logic - Computer Science Engineering (CSE) PDF Download

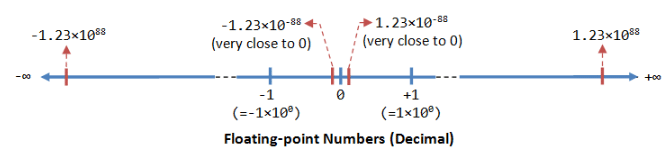
• A floating-point number (or real number) can represent a very large (1.23×10⁸⁸) or a very small (1.23×10^-88) value. It could also represent very large negative number (-1.23×10⁸⁸) and very small negative number (-1.23×10⁸⁸), as well as zero, as illustrated:
  
• A floating-point number is typically expressed in the scientific notation, with a fraction (F), and an exponent (E) of a certain radix (r), in the form of F×r^E. Decimal numbers use radix of 10 (F×10^E); while binary numbers use radix of 2 (F×2^E).
• Representation of floating point number is not unique. For example, the number 55.66 can be represented as 5.566×10¹, 0.5566×10², 0.05566×10³, and so on. The fractional part can be normalized. In the normalized form, there is only a single non-zero digit before the radix point. For example, decimal number 123.4567 can be normalized as 1.234567×10²; binary number 1010.1011B can be normalized as 1.0101011B×2³.
• It is important to note that floating-point numbers suffer from loss of precision when represented with a fixed number of bits (e.g., 32-bit or 64-bit). This is because there are infinite number of real numbers (even within a small range of says 0.0 to 0.1). On the other hand, a n-bit binary pattern can represent a finite 2ⁿ distinct numbers. Hence, not all the real numbers can be represented. The nearest approximation will be used instead, resulted in loss of accuracy.
• It is also important to note that floating number arithmetic is very much less efficient than integer arithmetic. It could be speed up with a so-called dedicated floating-point co-processor. Hence, use integers if your application does not require floating-point numbers.
• In computers, floating-point numbers are represented in scientific notation of fraction (F) and exponent (E) with a radix of 2, in the form of F×2E. Both E and F can be positive as well as negative. Modern computers adopt IEEE 754 standard for representing floating-point numbers. There are two representation schemes: 32-bit single-precision and 64-bit double-precision. 

IEEE-754 32-bit Single-Precision Floating-Point Numbers

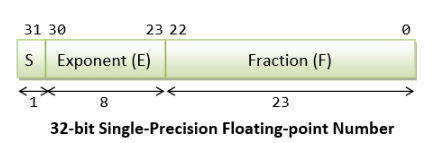
In 32-bit single-precision floating-point representation:

• The most significant bit is the sign bit (S), with 0 for positive numbers and 1 for negative numbers.
• The following 8 bits represent exponent (E).
• The remaining 23 bits represents fraction (F).

Normalized Form
Let's illustrate with an example, suppose that the 32-bit pattern is 1 1000 0001 011 0000 0000 0000 0000 0000, with:

S = 1

E = 1000 0001

F = 011 0000 0000 0000 0000 0000

In the normalized form, the actual fraction is normalized with an implicit leading 1 in the form of 1.F. In this example, the actual fraction is 1.011 0000 0000 0000 0000 0000 = 1 + 1×2^-2 + 1×2^-3 = 1.375D.
The sign bit represents the sign of the number, with S=0 for positive and S=1 for negative number. In this example with S=1, this is a negative number, i.e., -1.375D.
In normalized form, the actual exponent is E-127 (so-called excess-127 or bias-127). This is because we need to represent both positive and negative exponent. With an 8-bit E, ranging from 0 to 255, the excess-127 scheme could provide actual exponent of -127 to 128. In this example, E-127 = 129-127 = 2D.
Hence, the number represented is -1.375×2² = -5.5D.

De-Normalized Form
Normalized form has a serious problem, with an implicit leading 1 for the fraction, it cannot represent the number zero! Convince yourself on this!
De-normalized form was devised to represent zero and other numbers.
For E=0, the numbers are in the de-normalized form. An implicit leading 0 (instead of 1) is used for the fraction; and the actual exponent is always -126. Hence, the number zero can be represented with E=0 and F=0 (because 0.0 × 2^-126 = 0).
We can also represent very small positive and negative numbers in de-normalized form with E = 0. For example, if S = 1, E = 0, and F = 011 0000 0000 0000 0000 0000. The actual fraction is 0.011 = 1×2^-2 + 1 × 2^-3 = 0.375D. Since S = 1, it is a negative number. With E = 0, the actual exponent is -126. Hence the number is -0.375 × 2^-126 = -4.4 × 10^-39, which is an extremely small negative number (close to zero).

Summary
In summary, the value (N) is calculated as follows:

• For 1 ≤ E ≤ 254, N = (-1)^S × 1.F × 2^(E-127). These numbers are in the so-called normalized form. The sign-bit represents the sign of the number. Fractional part (1.F) are normalized with an implicit leading 1. The exponent is bias (or in excess) of 127, so as to represent both positive and negative exponent. The range of exponent is -126 to +127.
• For E = 0, N = (-1)^S × 0.F × 2^(-126). These numbers are in the so-called denormalized form. The exponent of 2^-126 evaluates to a very small number. Denormalized form is needed to represent zero (with F = 0 and E = 0). It can also represents very small positive and negative number close to zero.
• For E = 255, it represents special values, such as ±INF (positive and negative infinity) and NaN (not a number). This is beyond the scope of this article.

Example 1: Suppose that IEEE-754 32-bit floating-point representation pattern is 0 10000000 110 0000 0000 0000 0000 0000.

Sign bit S = 0 ⇒ positive number

E = 1000 0000B = 128D (in normalized form)

Fraction is 1.11B (with an implicit leading 1) = 1 + 1×2^-1 + 1×2^-2 = 1.75D

The number is +1.75 × 2^(128-127) = +3.5D

Example 2: Suppose that IEEE-754 32-bit floating-point representation pattern is 1 01111110 100 0000 0000 0000 0000 0000.

Sign bit S = 1 ⇒ negative number

E = 0111 1110B = 126D (in normalized form)

Fraction is 1.1B  (with an implicit leading 1) = 1 + 2^-1 = 1.5D

The number is -1.5 × 2^(126-127) = -0.75D

Example 3: Suppose that IEEE-754 32-bit floating-point representation pattern is 1 01111110 000 0000 0000 0000 0000 0001.

Sign bit S = 1 ⇒ negative number

E = 0111 1110B = 126D (in normalized form)

Fraction is 1.000 0000 0000 0000 0000 0001B  (with an implicit leading 1) = 1 + 2^-23

The number is -(1 + 2^-23) × 2^(126-127) = -0.500000059604644775390625 (may not be exact in decimal!)

Example 4: (De-Normalized Form): Suppose that IEEE-754 32-bit floating-point representation pattern is 1 00000000 000 0000 0000 0000 0000 0001.

Sign bit S = 1 ⇒ negative number

E = 0 (in de-normalized form)

Fraction is 0.000 0000 0000 0000 0000 0001B  (with an implicit leading 0) = 1×2^-23

The number is -2^-23 × 2^(-126) = -2×(-149) ≈ -1.4×10^-45

Exercises (Floating-point Numbers)

• Compute the largest and smallest positive numbers that can be represented in the 32-bit normalized form.

Largest positive number: S=0, E=1111 1110 (254), F = 111 1111 1111 1111 1111 1111.

Smallest positive number: S=0, E=0000 00001 (1), F = 000 0000 0000 0000 0000 0000.

• Compute the largest and smallest negative numbers can be represented in the 32-bit normalized form.

Same as above, but S=1.

• Repeat (1) for the 32-bit denormalized form.

Largest positive number: S=0, E=0, F=111 1111 1111 1111 1111 1111.

Smallest positive number: S=0, E=0, F=000 0000 0000 0000 0000 0001.

• Repeat (2) for the 32-bit denormalized form.

Same as above, but S=1.

Notes For Java Users
You can use JDK methods Float.intBitsToFloat(int bits) or Double.longBitsToDouble(long bits) to create a single-precision 32-bit float or double-precision 64-bit double with the specific bit patterns, and print their values. For examples,

System.out.println(Float.intBitsToFloat(0x7fffff));

System.out.println(Double.longBitsToDouble(0x1fffffffffffffL));

IEEE-754 64-bit Double-Precision Floating-Point Numbers

• The most significant bit is the sign bit (S), with 0 for positive numbers and 1 for negative numbers.
• The following 11 bits represent exponent (E).
• The remaining 52 bits represents fraction (F).

The value (N) is calculated as follows:

• Normalized form: For 1 ≤ E ≤ 2046, N = (-1)^S × 1.F × 2^(E-1023).
• Denormalized form: For E = 0, N = (-1)^S × 0.F × 2^(-1022). These are in the denormalized form.
• For E = 2047, N represents special values, such as ±INF (infinity), NaN (not a number).

More on Floating-Point Representation

• The sign bit (S) is self-explanatory (0 for positive numbers and 1 for negative numbers).
• For the exponent (E), a so-called bias (or excess) is applied so as to represent both positive and negative exponent. The bias is set at half of the range. For single precision with an 8-bit exponent, the bias is 127 (or excess-127). For double precision with a 11-bit exponent, the bias is 1023 (or excess-1023).
• The fraction (F) (also called the mantissa or significand) is composed of an implicit leading bit (before the radix point) and the fractional bits (after the radix point). The leading bit for normalized numbers is 1; while the leading bit for denormalized numbers is 0.

Normalized Floating-Point Numbers
In normalized form, the radix point is placed after the first non-zero digit, e,g., 9.8765D×10^-23D, 1.001011B×2¹¹B. For binary number, the leading bit is always 1, and need not be represented explicitly - this saves 1 bit of storage.
In IEEE 754's normalized form:

• For single-precision, 1 ≤ E ≤ 254 with excess of 127. Hence, the actual exponent is from -126 to +127. Negative exponents are used to represent small numbers (< 1.0); while positive exponents are used to represent large numbers (> 1.0).
  N = (-1)^S × 1.F × 2^(E-127)
• For double-precision, 1 ≤ E ≤ 2046 with excess of 1023. The actual exponent is from -1022 to +1023, and
  N = (-1)^S × 1.F × 2^(E-1023)

Take note that n-bit pattern has a finite number of combinations (= 2ⁿ), which could represent finite distinct numbers. It is not possible to represent the infinite numbers in the real axis (even a small range says 0.0 to 1.0 has infinite numbers). That is, not all floating-point numbers can be accurately represented. Instead, the closest approximation is used, which leads to loss of accuracy.
The minimum and maximum normalized floating-point numbers are:

Denormalized Floating-Point Numbers
If E = 0, but the fraction is non-zero, then the value is in denormalized form, and a leading bit of 0 is assumed, as follows:

• For single-precision, E = 0,
   N = (-1)^S × 0.F × 2^(-126)
• For double-precision, E = 0,
  N = (-1)^S × 0.F × 2^(-1022)

Denormalized form can represent very small numbers closed to zero, and zero, which cannot be represented in normalized form, as shown in the above figure.
The minimum and maximum of denormalized floating-point numbers are:

Special Values

• Zero: Zero cannot be represented in the normalized form, and must be represented in denormalized form with E=0 and F=0. There are two representations for zero: +0 with S=0 and -0 with S=1.
• Infinity: The value of +infinity (e.g., 1/0) and -infinity (e.g., -1/0) are represented with an exponent of all 1's (E = 255 for single-precision and E = 2047 for double-precision), F=0, and S=0 (for +INF) and S=1 (for -INF).
• Not a Number (NaN): NaN denotes a value that cannot be represented as real number (e.g. 0/0). NaN is represented with Exponent of all 1's (E = 255 for single-precision and E = 2047 for double-precision) and any non-zero fraction.