Fluid Kinematics | Fluid Mechanics for Mechanical Engineering PDF Download
| Table of contents |

|
| What is Fluid Kinematics? |

|
| Different Flow Pattern |

|
| Velocity of a Fluid Particle |

|
| What is Stream Function? |

|
| Velocity Potential Function |

|
What is Fluid Kinematics?
Fluid Kinematics involves the study of fluid motion, encompassing factors like displacement, velocity, acceleration, and other related aspects. This subject holds significance in both exam preparation and enhancing the candidate's understanding. Kinematics, a branch of classical mechanics, is concerned with delineating the motion of bodies and systems, excluding any consideration of the forces driving the motion.
Types of Fluid Flows
Fluid flow can be classified into different categories based on various parameters. These types of fluid flow are done on parameters consisting of the nature of the flow, flow patterns etc. Fluid flow may be classified under the following headings;
Steady & Unsteady Flow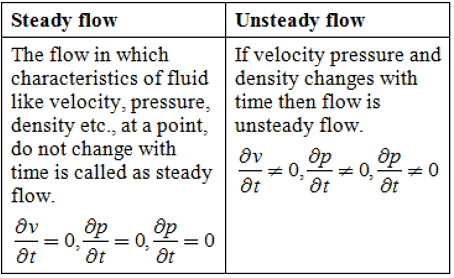
Uniform & Non-uniform Flow

Laminar & Turbulent Flow
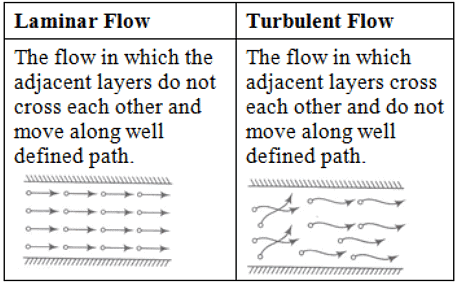
Rotational & Irrotational Flow

Combining these, the most common flow types in Fluid Kinematics are:
Steady uniform flow
Conditions do not change with position in the stream or with time.
Example: flow of water in a pipe of constant diameter at a constant velocity.
Steady non-uniform flow
Conditions change from point to point in the stream but do not change with time.
Example: Flow in a tapering pipe with the constant velocity at the inlet.
Unsteady uniform flow
At a given instant, the conditions at every point are the same but will change with time.
Example: A pipe of constant diameter connected to a pump pumping at a constant rate which is then switched off.
Unsteady non-uniform flow
Every flow condition may change from point to point and with time at every point.
Example: Waves in a channel
Different Flow Pattern
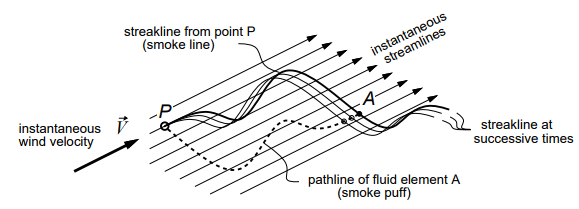
Three fluid element trajectories are defined: Streamlines, Pathlines, and Streaklines. These flow patterns depend on the fluid particle’s motion
- Pathline represents the real trajectory covered by a specific fluid particle within a given time interval. For a fluid element labeled as A, its pathline essentially denotes the route it follows in space with respect to time. An instance of a pathline can be observed in the course taken by a single puff of smoke transported by either a consistent or fluctuating wind.
- Streamline is a line that tangentially aligns with the velocity field at every point. Streamlines can be derived through analytical methods by integrating equations that describe lines tangent to the velocity field, such as the equation dy/dx = v/u,
where u, v, and w represent the velocity components in the x, y, and z directions, respectively. - A streakline is the path traced by particles that have previously passed through a specified point. It is linked to a specific point, P, in space where the fluid flows past. The streakline of point P consists of all the points that have passed through it. A practical illustration of a streakline is the unbroken line of smoke released from a chimney at point P, which may exhibit a curved shape if the wind direction varies over time.
- Streamtube: The surface of a streamtube is constituted by the collection of streamlines passing through various points. Since there is no flow across this surface, each cross-section of the streamtube carries an identical mass flow. Therefore, the streamtube can be likened to a channel flow integrated within the larger flow field.
- The figure below illustrates streamlines, pathlines, and streaklines for the case of smoke being continuously emitted by a chimney at point P in the presence of shifting wind.
- In a steady flow, streamlines, pathlines, and streaklines all coincide.
- In this example, they would all be marked by the smoke line.
Velocity of a Fluid Particle
The velocity of a fluid particle is defined as the displacement of the particle over a given time period. The fluid flow's velocity may vary along different directions and is denoted as u, v, and w in the x, y, and z axes, respectively.
- The velocity of the fluid along any direction can be defined as the rate of change of displacement of the fluid along that direction.
- Let V be the resultant velocity of the fluid along any direction, and u, v and w be the velocity components in the x, y and z directions, respectively.
- Mathematically the velocity components can be written as
u = f ( x, y, z, t )
w = f ( x, y, z, t )
v = f ( x, y, z, t )
- Let VR is the resultant velocity at any point in a fluid flow.
- Resultant velocity VR= ui + vj + wk
VR = √(u2+ v2 + w2)
Where u=dx/dt, v=dy/dt and w=dz/dt are the resultant vectors in X, Y and Z directions, respectively.
Acceleration of Fluid Particle
The acceleration of a fluid particle is the rate of change of its velocity over time. Acceleration can be categorized into temporal acceleration and convective acceleration.
Acceleration of a fluid element along any direction can be defined as the rate of change of velocity of the fluid along that direction.
If ax, ay and az are the acceleration components along the x, y and z directions, it can be mathematically written as ax = du/ dt.

What is Stream Function?
The stream function is a valid mathematical function used to describe the fluid flow in the two dimensions flow. It will be explained below.
The partial derivative of the stream function to any direction gives the velocity component at right angles to that direction. It is denoted by ψ.
∂Ψ/∂x = v, ∂Ψ/∂y = -u
The continuity equation for two-dimensional flow is
(∂2Ψ/∂y.∂x + ∂2Ψ/∂x.∂y) = 0
Equations of Rotational Flow
Equations of rotational flow are used to describe the rotational characteristics of the flow. With the help of rotational velocity ω, the rotational characteristics of a flow can be categorized.
- As ψ satisfies the continuity equation, if ψ exists, it is a possible case of fluid flow.
- Rotational components of fluid particles are:
ωz = 1/2(∂w/∂y – ∂v/∂z)
ωz = 1/2(∂u/∂z – ∂w/∂x)
ωz = 1/2(∂v/∂x – ∂u/∂x)
Equation of Irrotational Flow
- If ωx = ωy = ωz, then the flow is irrotational.
- For irrotational flow, ωz = 0
ωz = 1/2(∂v/∂x – ∂u/∂y) = 1/2(∂(-∂Ψ/∂x)/∂x – ∂(-∂Ψ/∂y)/∂y) = 1/2(∂2Ψ/∂x2 – ∂2Ψ/∂y2)
- This is the Laplace equation for ψ.
Note: It can be concluded that if stream function (ψ) exits, it is a possible case of fluid flow. But we can’t decide whether the flow is rotational or irrotational. But if stream function ψ satisfies the Laplace equation, it is a possible case of irrotational flow. Otherwise, it is a rotational flow.
Velocity Potential Function
The velocity potential function is a mathematical expression utilized to depict the flow attributes of a fluid, including those of a three-dimensional flow. It provides a detailed description of various characteristics of the fluid flow.
- It is a scalar function of space and time such that its negative derivative to any direction gives the fluid velocity in that direction. It is denoted b φ
-∂Φ/∂x = u, ∂Φ/∂y = -v, ∂Φ/∂z = -w
We know that the continuity equation for steady flow is
∂u/∂x + ∂v/∂y = 0
∂(-∂Φ/∂x)/∂x + ∂(-∂Φ/∂y)/∂y = 0
∂2Φ/∂x2 + ∂2Φ/∂y2 = 0
If φ satisfies the Laplace equation, it is a possible case of fluid flow.
Rotational component (ωz) can be given by
ωz = 1/2(∂v/∂x – ∂u/∂y) = 1/2(∂(-∂Φ/∂y)/∂x – ∂(-∂Φ/∂x)/∂y) = 1/2(∂2Φ/∂y.∂x – ∂2Φ/∂x.∂y)
- It shows that φ exits. Then, the flow will be irrotational.
Relation between Stream Function and Velocity Potential Function
In fluid kinematics, the stream function and velocity potential function are mathematical functions employed to elucidate distinct flow characteristics. Stream functions describe two-dimensional flow, while the velocity potential function is applicable to three-dimensional flow as well. The following sections provide explanations for these terms.
The velocity potential function can be written as
dΦ/dx = -u
dΦ/dy = -v
and stream function can be written as
dψ/dx = v
dψ/dy = -u
So, dψ/dx = dΦ/dy
dΦ/dx = dψ/dy
Stream versus Velocity Potential Function

Equipotential Line versus StreamLine

|
56 videos|104 docs|75 tests
|
FAQs on Fluid Kinematics - Fluid Mechanics for Mechanical Engineering
| 1. What is fluid kinematics? |  |
| 2. What is a stream function in fluid mechanics? |  |
| 3. How is a velocity potential function related to fluid kinematics? |  |
| 4. What are some common applications of fluid kinematics in mechanical engineering? |  |
| 5. How can fluid kinematics be used to optimize the performance of a fluid system? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|
















