Forced Oscillator | Oscillations, Waves & Optics - Physics PDF Download
Forced Oscillations and Resonance
When a body is made to oscillate under external periodic force, then in the beginning the body tries to oscillate with its natural frequency, but very soon these oscillation dies out and the body oscillate with the frequency of the applied force. Such oscillation is called forced oscillation.
Example:
1) Person swinging in a swing without anyone pushing → Free or damped oscillation
2) Someone pushes the swing periodically → Forced or driven oscillations
Natural angular frequency (ω0) of the system when system oscillates freely after a sudden disturbance.
External frequency( p) of the system is the angular frequency of the external driving force causing the driven oscillations.
Resonance
When the frequency of the external force is same as the natural frequency of the body, the amplitude of the oscillation is maximum. This phenomenon is called resonance.
Transient Effect
In the presence of external periodic force, initially body tries to oscillate with its natural frequency, while external force tries to impose its own frequency. Thus there is a tussel between external force and the body during which the amplitude rises and falls alternatively. This is the transient effect which soon dies out and body start oscillating with external frequency.
Equation of Forced Oscillation
Consider a mass m oscillating under external periodic force F. let x be the displacement at any instant. The forces acting on the mass are
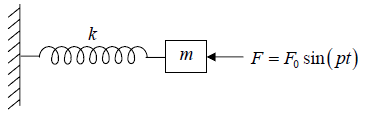
(i) Restoring force proportional to the displacement. This is written as F = −kx
(ii) A frictional force proportional to the velocity. This is written as Fres = 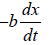
(iii) An external periodic force, which is F = F0 sin (pt)
Thus the total force on the body is F = 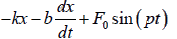
Using newton’s third law, we can write 
where 2γ = b/m, ω02 = k/m and 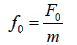
This is the differential equation of the forced harmonic oscillator.
General solution of the differential equation: Once the transient effect dies out, body starts oscillating with frequency of the external force. So we can assume a solution of differential equation as x = Asin ( pt −θ )
Differentiating and putting in differential equation we obtain the value of amplitude A
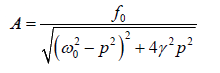
phase difference θ between the displacement and the driving force is tanθ = 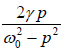
Thus solution of the forced oscillator becomes x = 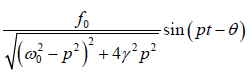
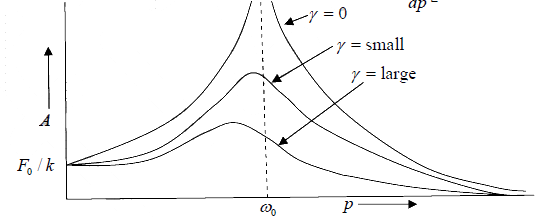
Amplitude Resonance
The amplitude A of the forced oscillator depends on the constant f0 and p of the driving force and the constant ω0 and γ of the oscillator. At certain driving frequency amplitude A becomes maximum that is called amplitude resonance. Three different cases arise
Case 1: At very low driving frequency( p <<ω0 ). The amplitude A turns to be

This shows that the amplitude depends only upon force constant and independent of mass, damping constant and driving frequency.
Case 2: At very high frequency( )0 p >>ω , we get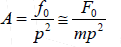
This shows that amplitude now depends upon mass and driving frequency.
Case 3: Amplitude will be maximum when the denominator 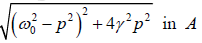 is minimum. So that its first derivative coefficient will be zero
is minimum. So that its first derivative coefficient will be zero 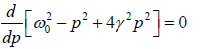
This gives the corresponding driving frequency i.e. amplitude resonance frequency at
which A is maximum is p = 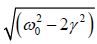 .
.
At this frequency the amplitude is Amax = 
This shows that maximum amplitude depends upon the damping constant , smaller the
damping larger is the amplitude. When, max γ = 0, Amax→ ∞.
Dependence of the phase of displacement on the frequency of driving force
In steady state condition, the force equation and displacement equation is
F = F0sin(pt ) and x = Asin ( pt −θ ) , the phase factor is tanθ = 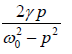 .
.
This indicates that the displacement of the forced oscillation lags behind the driving force F0 sin(pt) by an angleθ . The phase difference θ depends upon the damping γ and also on the difference between natural and driving frequency.
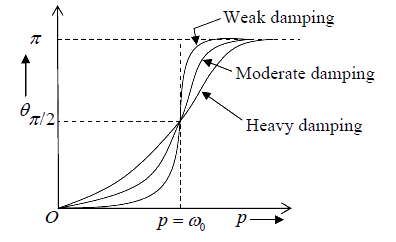
Case 1: If 0 p <<ω , than tanθ is positive and θ lies between 0 and π/2 . In this condition
(whenγ ≈ 0 ), θ is nearly zero i.e. displacement is in phase with driving force
Case 2: If 0 p =ω , than tanθ is infinite and θ =π/2 . This is the resonance condition, displacement always lag behind the force by π/2. It means that at resonance the displacement is minimum when the driving force is maximum and vice versa.
Case 3: If 0 p >>ω , than tanθ is negative and θ lies between π/2 and π . In this condition, θ is nearly π i.e. displacement almost opposite in phase with the driving force. The variation of θ with driving frequency p is given below.
Velocity Resonance
Velocity of the body also depends on the constant 0 f and p of the driving force and the constant ω0 and γ of the oscillator. At certain driving frequency velocity amplitude becomes maximum that is called velocity resonance.
The instantaneous velocity of the body is
u = 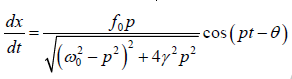
The velocity will be maximum when cos ( pt −θ ) =1. The maximum value is known as
“velocity amplitude” u0 . Thus
u0 = 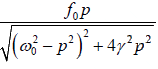
Three different cases arise.
Case 1: At very low driving frequency ( ) 0 p <<ω . The velocity amplitude u0 turns to be
u0 = 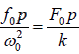
This indicates that the velocity amplitude depends on the spring constant k .
Case 2: At very high frequency( )0 p >>ω , we get u0 = 
It shows that velocity amplitude depends on mass as well as driving frequency.
Case 3: At certain frequency the velocity amplitude becomes maximum, that frequency
is called the velocity resonance frequency. The velocity amplitude can be written as
u0 = 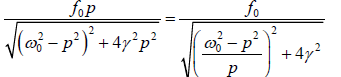
The velocity amplitude u0 will be maximum when the denominator 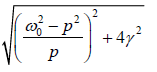
is minimum i.e. when
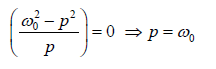
This shows that the velocity resonance irrespective of damping value, always occurs when driving frequency is equal to the natural undamped frequency of the body.
The velocity amplitude at the resonance is u0 = 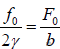
This shows that velocity amplitude at resonance only depends on the damping constant. Dependence of the velocity of a forced oscillator on the driving frequency is shown as below
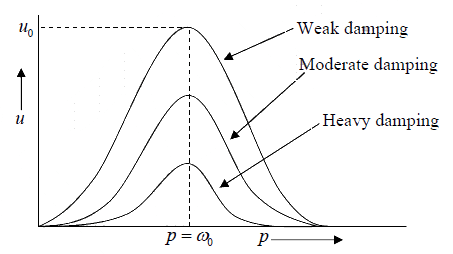
Dependence of the phase of velocity on the frequency of driving force:
In steady state condition, the force equation and velocity equation is
F = F0 sin(pt)
u = 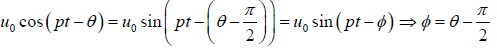
⇒ 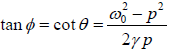
∵ tanθ = 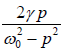
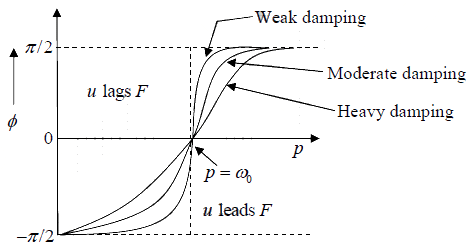
Case 1: If p <<ω0 , than tanθ is positive and θ lies between 0 and π/2. In this condition (whenγ ≈ 0 ), θ is nearly zero. Thus φ = -π/2, this means velocity leads the driving force.
Case 2: If 0 p =ω , than tanθ is infinite and π/2θ = , and φ = 0 , this means that at resonance, the velocity is always in phase with the driving force.
Case 3: If 0 p >>ω , than tanθ is negative and θ lies between π/2and π , so that the φ is
positive. This means that velocity lags behind the driving force.
The dependence of phase of velocity of the body on the frequency of the driving force is
shown below.
Average power absorbed by oscillator (supplied by the driving force)
An oscillator absorbed energy from the driving force which is dissipated in doing work against the damping force present.
The instantaneous power P (i.e. rate at which work is done) absorbed by the oscillator is
equal to energy per unit time.
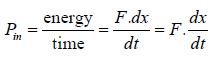
Thus in Pin is equal to the product of the instantaneous driving force and the instantaneous velocity.
Thus
Pin = 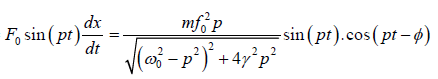
= 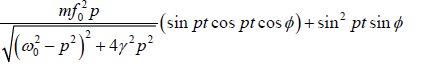
Now the average power absorbed is (Pin) = 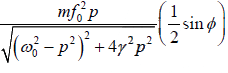
Note: the average values of the periodic function for the one period T = 2π/p is
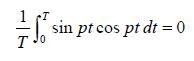 and
and 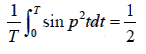
Since, tanθ = 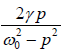 , thus using the vector model
, thus using the vector model
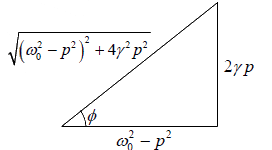
sinφ = 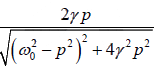
Therefore, the average power absorbed by the oscillator (average power supplied by the
driving force) is
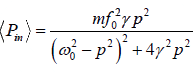
The power supplied by the driving force is not stored in the system, but is dissipated as
work done in moving the system against the force of friction.
Power Dissipated through frictional force
The instantaneous power dissipated through friction is given by
Pdis = |instantaneous frictional force| x |instantaneous velocity|
= 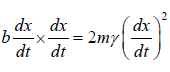 =
= 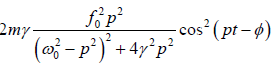
Now the average of cos2( pt −φ ) for one full period is 1/2. Therefore the average power dissipated is 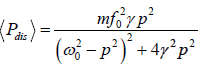
Thus in (Pin) = (Pdis)
This shows that in the steady state the average power supplied by the driving force is equal to the average power dissipated by the frictional force.
Note: The instantaneous input power is not equal to the instantaneous power dissipated.
Therefore at any instant of time the power stored in the oscillator is not constant.
Maximum power absorption
The average power can also be written as
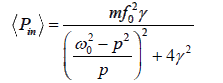
(Pin) will be maximum when the denominator 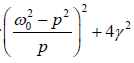 is a minimum, this occurs when ω02 − p2 = 0 or p =ω0
is a minimum, this occurs when ω02 − p2 = 0 or p =ω0
this is the condition of velocity resonance. Hence the power transferred from the driving force is maximum at the frequency of velocity resonance. The maximum power is
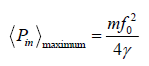
Sharpness of Resonance and Bandwidth
Sharpness of Resonance
The rapidity with which the power falls from its resonant value with change in a driving frequency is known as Sharpness of resonance.
The average power is maximum at certain frequency. As the driving frequency deviates either way from its resonant value, the power falls from its maximum value. If the fall in power with change in driving frequency from the resonant value is large, the resonance is said to be sharp, on the other hand, the fall is small, the resonant is said to be flat.
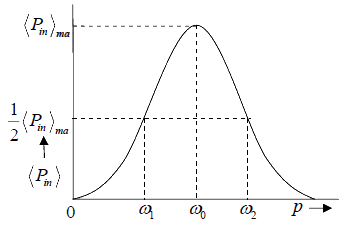
It is measured by the ratio of the resonant frequency ω0 to the difference of two frequencies ω1 and ω2 at which the power falls to half of the resonant value.
Sharpness of resonance = ω0/ω2-ω1
Bandwidth of Resonance
The difference in values of the driving frequency, at which the average power absorbed
drops to half its maximum value, is called the band width of the resonance.
Bandwidth = ω2-ω1
The average power absorbed is
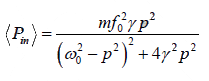
The maximum average power is
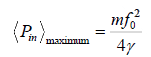
The variation of the average power with driving frequency is shown in above figure also shows the half power frequencies.
The value of p at which the power goes half the maximum value obtained as
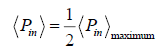 ⇒
⇒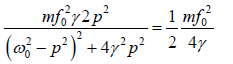
or 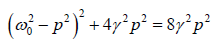 ⇒
⇒ 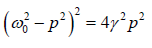
or ω02 − p2 = ± 2γp ⇒ p2 =ω02 ± 2γp
These are two quadratic equations in p ,
p2 + 2γp + ω02 = 0 and p2 - 2γp - ω02 = 0
each has two roots one positive and other negative. Since negative frequency are not
allowed, thus the allowed positive roots are
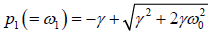 and
and 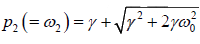
The frequency difference between tow half power points i.e. bandwidth is
Bandwidth = ω2 - ω1 = 2γ = 1/t and sharpness of resonance
= 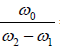 = ω0t
= ω0t
It indicates that smaller the bandwidth, sharper is the resonance.
Quality Factor
The quality factor is defined as Q = 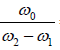 = Resonance frequency/bandwidth = ω0t
= Resonance frequency/bandwidth = ω0t
Quality factor also defined as
Q = 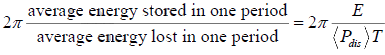
Where (Pdis) is the average power dissipated and T is the time period of oscillation. Thus (Pdis) x T is the average energy lost in one period. On solving for energy we get the following expression of the quality factor.
Q = 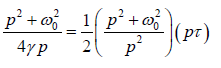
This is the exact expression for the quality factor of forced oscillator.
Near resonance, p =ω0 , so we get Q =ω0τ
|
54 videos|22 docs|14 tests
|
FAQs on Forced Oscillator - Oscillations, Waves & Optics - Physics
| 1. What is resonance in the context of forced oscillations? |  |
| 2. What is the transient effect in forced oscillations? |  |
| 3. What is the equation of forced oscillation? |  |
| 4. What is amplitude resonance? |  |
| 5. How does the phase of velocity depend on the frequency of the driving force in forced oscillations? |  |





















