Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Forming Equations
Forming Equations | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Forming Equations
Before solving an equation you may need to form it from the information given in the question.
How do I form an expression?
- An expression is an algebraic statement lacking an equals sign, like 3x+7 or 2(x2 −14).
- At times, we create expressions to aid in expressing unknown values.
- When a value is unidentified, it can be denoted by a letter such as x.
- Common phrases can be transformed into expressions.
- In this context, the "something" can be symbolized by any letter.

- In this context, the "something" can be symbolized by any letter.
- You may need to utilize brackets to indicate the correct order of operations.
- To express "something" added by 1 and then multiplied by 3, it's represented as 3(x + 1).
- For "something" multiplied by 3 and then added by 1, it's written as 3x + 1.
- To simplify expressions, opt for the smallest value to be symbolized by a letter.
- For instance, if Adam is 10 years younger than Barry, then Barry's age is x + 10 if Adam's age is represented by x. This approach simplifies the algebra, rather than assigning x to Barry's age and x − 10 to Adam's age.
- Similarly, if Adam's age is half of Barry's age, then Barry's age is double that of Adam's. So, if Adam's age is x, Barry's age is 2x. This simplifies the algebra, rather than using x for Barry's age and
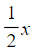 for Adam's age.
for Adam's age.
How do I form an equation?
- An equation is a mathematical expression that contains an equals sign and can be solved.
- To solve an equation, you need to create an expression that is equal to a value or another expression.
- It's helpful to be familiar with different words that represent basic mathematical operations:
- For addition: sum, total, more than, increase, etc.
- For subtraction: difference, less than, decrease, etc.
- For multiplication: product, lots of, times as many, double, triple, etc.
- For division: shared, split, grouped, halved, quartered, etc.
- Using the first example above:
- If Adam is 10 years younger than Barry and the sum of their ages is 25, you can find out how old each one is
- Represent Adam's age as x then Barry's age is x + 10
- We can solve the equation x + x + 10 = 25 or 2 x + 10 = 25
- If Adam is 10 years younger than Barry and the sum of their ages is 25, you can find out how old each one is
- Sometimes you might have two unrelated unknown values (x and y) and have to use the given information to form two simultaneous equations
Forming Equations from Shapes
Many questions involve having to form and solve equations from information given about things relating to shapes, like lengths or angles.
How do I form an equation involving the area or perimeter of a 2D shape?
- Read the question attentively to determine if it pertains to area, perimeter, or angles.
- If no visual aid is provided, consider sketching a diagram swiftly.
- Incorporate any details from the question into the diagram, typically involving expressions with one or two variables.
- For questions concerning perimeter, identify and sum up sides of equal length. Analyze the shape's properties to determine sides of equal length:
- In a square or rhombus, all four sides are equal.
- In a rectangle or parallelogram, opposite sides are equal.
- For triangles, check if any sides are of equal length.
- When dealing with area, note down the appropriate formula for the shape's area. For irregular shapes, consider breaking them down into simpler parts to calculate their areas effectively. Ensure to adjust the length and width accordingly.
- Remember, a regular polygon implies all sides are of equal length. For instance, a regular pentagon with side length 2x - 1 has 5 equal sides, making its perimeter 5(2x - 1).
- If a circle or a segment of a circle is involved, use the symbol π consistently instead of multiplying by it, which might result in lengthy decimals.
How do I form an equation involving angles in a 2D shape?
- If no diagram is given it is almost always a good idea to quickly sketch one
- Add any information given in the question to the diagram
- This information will normally involve expressions in terms of one or two variables
- Consider the properties of angles within the given shape to decide which sides will have equal lengths
- If a triangle is given, how many of the angles are equal?
- An isosceles triangle has two equal angles
- An equilateral triangle has three equal angles
- Consider angles in parallel lines (alternative, corresponding, co-interior)
- In a parallelogram or rhombus, opposite angles are equal and all four sum to 360°
- A kite has one equal pair of opposite angles
- If a triangle is given, how many of the angles are equal?
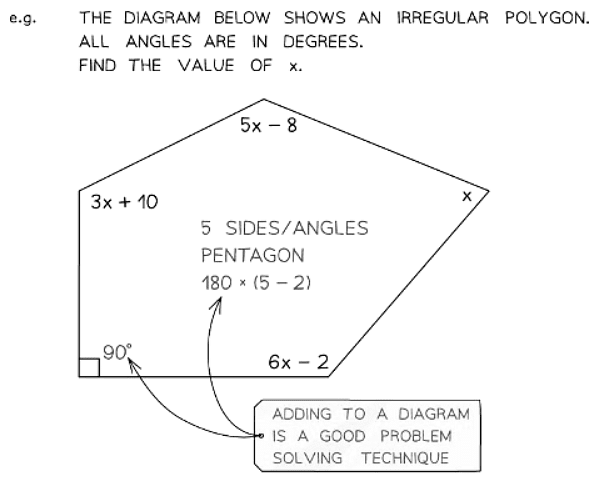
- If the question involves angles, use the formula for the sum of the interior angles of a polygon
- For a polygon of n sides, the sum of the angles will be 180°×(n - 2)
- Remember that a regular polygon means all the angles are equal
- If a question involves an irregular polygon, assume all the angles are different unless told otherwise
- Look out for key information that can give more information about the angles
- For example, a trapezium "with a line of symmetry" will have two pairs of equal angles

How do I form an equation involving the surface area or volume of a 3D shape?
- Read the question carefully to decide if it involves surface area or volume
- Mixing these up is a common mistake made in GCSE exams
- If no diagram is given it is almost always a good idea to quickly sketch one
- Add any information given in the question to the diagram
- This information will normally involve expressions in terms of one or two variables
- Consider the properties of the given shape to decide which sides will have equal lengths
- In a cube all sides are equal
- All prisms have the same shape (cross section) at the front and back
- Pyramids normally have 1/3 in the formula
- If the question involves volume, write down the necessary formula for the area of that shape
- If it is an uncommon shape the exam question will give you the formula that you need
- Substitute the expressions for the side lengths into the formula
- Remember to include brackets around any expression that you substitute in
- It the question involves surface area,
- STEP 1: Write down the number of faces the shape has and if any are the same
- STEP 2: Identify the 2D shape of each face and write down the formula for the area of each one
- STEP 3: Substitute the given expressions into the formula for each one, being careful to identify the correct expression for the dimension
- You may need to add or subtract some expressions
- STEP 4: Add the expressions together, double checking that you have one for each of the faces
- Remember to consider any faces that may be hidden in the diagram
The document Forming Equations | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
FAQs on Forming Equations - Mathematics for GCSE/IGCSE - Class 10
| 1. How can I form equations from shapes in geometry problems? |  |
Ans. To form equations from shapes in geometry problems, you need to analyze the given information carefully and identify the relationships between the different elements of the shape. You can use variables to represent unknown quantities and then use the geometric formulas relevant to the shape to set up the equations.
| 2. Can you explain the steps involved in problem-solving using simultaneous equations? |  |
Ans. To solve problems using simultaneous equations, you first need to identify the unknown quantities and assign variables to them. Then, set up two or more equations based on the given information. Next, use algebraic methods such as substitution or elimination to solve the system of equations and find the values of the unknown quantities.
| 3. How do I understand age relationships in algebraic equations? |  |
Ans. Age relationships in algebraic equations involve representing the ages of individuals at different points in time using variables. By setting up equations based on the given information about the ages and relationships between the individuals, you can solve for the unknown ages. It is important to consider factors such as age differences and time elapsed.
| 4. What are some strategies for solving geometry problems involving shapes and formulas? |  |
Ans. Some strategies for solving geometry problems involving shapes and formulas include identifying the geometric properties of the shape, using relevant formulas to calculate lengths, angles, areas, and volumes, and breaking down complex shapes into simpler components. Visualization and drawing diagrams can also help in understanding the problem better.
| 5. How can I improve my understanding of expressions in algebra and formulating equations? |  |
Ans. To improve your understanding of expressions in algebra and forming equations, practice solving a variety of algebraic problems, familiarize yourself with common algebraic terms and symbols, and work on translating word problems into mathematical expressions. It is helpful to break down complex problems into smaller steps and seek help from teachers or online resources when needed.
Related Searches
















