Formulas: Trigonometry Formulas and Identities | Quantitative Aptitude for SSC CGL PDF Download
Trigonometry Formula
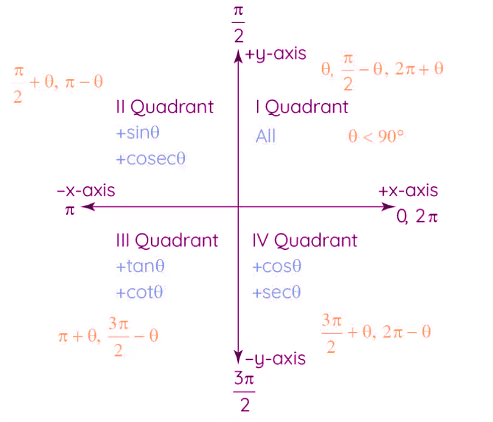
Trigonometry explores the connections between the angles and sides of triangles, with "Trigon" referring to triangle and "metry" to measurement. Trigonometry formulas offer a means to solve intricate problems that involve angles, distances, and various geometric concepts. This compilation encompasses all trigonometry formulas, along with a table containing function values.
Trigonometry Table
Before delving into trigonometry mathematical formulas, it is essential to grasp the meaning of the trigonometry table. The term "trigonometry" comprises two components: "trigon," signifying triangle, and "metry," signifying measurement. Thus, trigonometry fundamentally involves the measurement and comprehension of triangles. Presented below is a chart containing commonly used angle formulas in trigonometry to facilitate problem-solving.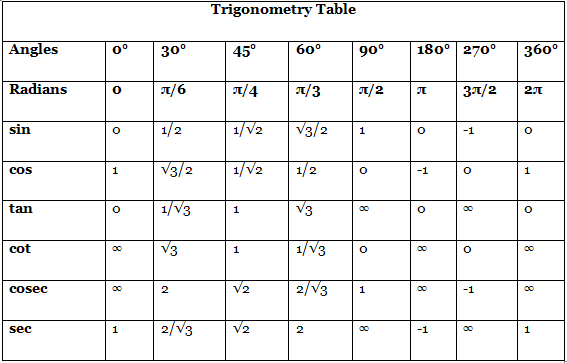
Trigonometric Ratios
Trigonometry ratios establish connections between angles and sides within triangles. Sine (sin) is defined as the ratio of the opposite side to the hypotenuse, cosine (cos) as the ratio of the adjacent side to the hypotenuse, and tangent (tan) as the ratio of the opposite side to the adjacent side. These ratios are instrumental in solving triangle-related problems and modeling wave phenomena across diverse fields, such as physics and engineering. Let's delve into the Trigonometric ratios for Right Triangles.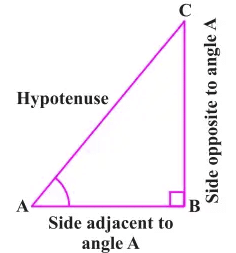
Basic Trigonometry Functions Formula
The 6 basic trigonometric functions are sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot). Here are trigonometric functions, identities, and some basic formulas:
- sin θ = Opposite Side/Hypotenuse
- cos θ = Adjacent Side/Hypotenuse
- tan θ = Opposite Side/Adjacent Side
- sec θ = Hypotenuse/Adjacent Side
- cosec θ = Hypotenuse/Opposite Side
- cot θ = Adjacent Side/Opposite Side
Trigonometric Ratios for Unit Circle
The unit circle's trigonometric ratios revolve around angles and coordinates, where sine (sin) represents the y-coordinate, cosine (cos) corresponds to the x-coordinate, and tangent (tan) is the ratio of sin to cos. These ratios offer valuable perspectives on circular motion, periodic functions, and complex numbers, playing a critical role in disciplines such as mathematics, physics, and engineering.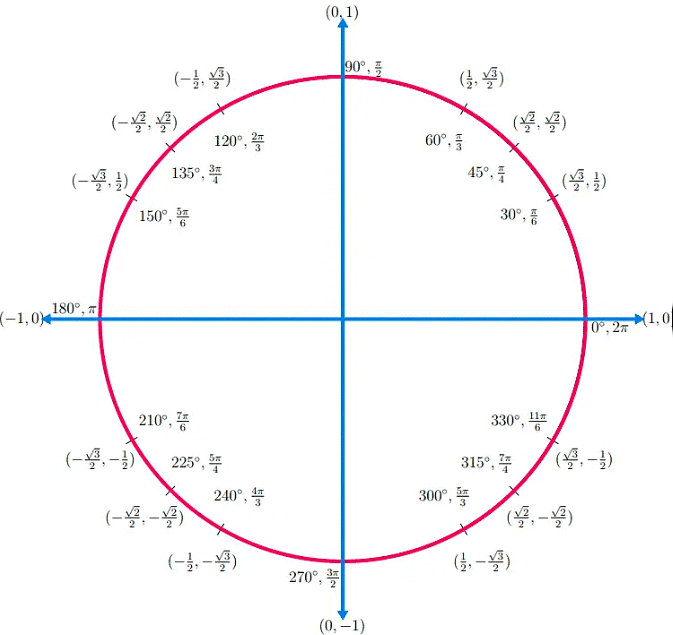
Generally, for a unit circle, the radius equals 1, and θ is the angle. The value of the hypotenuse and adjacent side here is equal to the radius of the unit circle.
Hypotenuse = Adjacent side to θ = 1
Therefore, the ratios of trigonometry are given by:
- sin θ = y/1 = y
- cos θ = x/1 = x
- tan θ = y/x
- cot θ = x/y
- sec θ = 1/x
- cosec θ = 1/y
Trigonometry Identities
Trigonometric identities form essential equations that define connections between various trigonometric functions. These equations remain valid for all angles and serve to streamline expressions and solve equations that incorporate trigonometric functions. Trigonometry employs specialized techniques known as "identities" to address challenging problems, providing useful tools that facilitate the quicker and easier resolution of complex trigonometric questions. Let's delve into some key identities together.
Reciprocal and Quotient Identities
Reciprocal and Quotient Identities provide relationships between the trigonometric functions which are discussed below.
Reciprocal Identities
Cosecant (cosec) is 1/sin, Secant (sec) is 1/cos, and Cotangent (cot) is 1/tan. These relationships link trigonometric functions and their reciprocals, helping simplify expressions and solve equations in trigonometry.
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
Quotient Identities
Tangent Identity tan θ = sin θ / cos θ and Cotangent Identity cot θ = 1 / tan θ (cos θ / sin θ), provide connections between tangent, cotangent, sine, and cosine functions.
Ranges of the Trigonometric Functions
The ranges of the trigonometry function sine, cosine, tangent, cotangent, secant and cosecant are as follows:
- −1 ≤ sin θ ≤ 1
- −1 ≤ cos θ ≤ 1
- −∞ ≤ tan θ ≤ ∞
- csc θ ≥ 1 and csc θ ≤ −1
- sec θ ≥ 1 sec θ ≤ −1
- −∞ ≤ cot θ ≤ ∞
Pythagorean Identities
The Pythagorean theorem serves as the basis for Pythagorean identities in Trigonometry, establishing connections between the trigonometric functions of an angle within a right triangle. The Pythagorean Theorem itself asserts that in a right triangle, the square of the hypotenuse's length equals the sum of the squares of the lengths of the other two sides. The Pythagorean identity specifically correlates the sine and cosine functions of an angle in trigonometry.
Pythagorean identities state that sin²θ + cos²θ = 1 and csc²θ – cot²θ = 1, connecting trig functions in a right angle triangle. These fundamental equations are used extensively in trigonometry to establish relationships between sine, cosine, secant, cosecant, and cotangent.
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = cosec²θ
Even and Odd Angle Formulas
- sin(-θ) = -sinθ
- cos(-θ) = cosθ
- tan(-θ) = -tanθ
- cot(-θ) = -cotθ
- sec(-θ) = secθ
- cosec(-θ) = -cosecθ
Co-function Formulas
- sin(90°-θ) = cos θ
- cos(90°-θ) = sin θ
- tan(90°-θ) = cot θ
- cot(90°-θ) = tan θ
- sec(90°-θ) = cosec θ
- cosec(90°-θ) = sec θ
Sum & Difference Identities
- sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
- cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
- sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
- cos(a-b)=cos(a)cos(b)+sin(a)sin(b)


Double Angle Formulas
- sin (2θ) = 2sinθ cosθ
= 2tanθ/1+tan²θ - cos (2θ) = cos²θ – sin²θ
= 2cos²θ – 1
= 1 – 2sin²θ - tan2θ = 2 tanθ / 1-tan²θ
Half Angle Formulas
Triple Angle Formulas
- sin 3θ = 3sinθ – 4sin³θ
- cos 3θ = 4cos³θ – 3cosθ

Product to Sum Formulas
- sin a sin b = 1/2 [cos (a-b) – cos (a+b)]
- cos a cos b = 1/2 [cos (a+b) + cos (a-b)]
- sin a cos b = 1/2 [sin (a+b) + sin (a-b)]
- cos a sin b = 1/2 [sin (a+b) – sin (a-b)]
Angle Sum and Difference Formulas
Angle Sum and Difference Formulas are also known as sum Product Formulas. These formulas allow you to express the trigonometric functions of sums and differences of angles.
Sum of Angles Formulas:
Difference of Angles Formulas:
Periodic Formulas
If n is an integer, then
sin(θ + 2πn) = sin θ
cos(θ + 2πn) = cos θ
tan(θ + πn) = tan θ
csc(θ + 2πn) = csc θ
sec(θ + 2πn) = sec θ
cot(θ + πn) = cot θ
Inverse Trigonometry Formulas and Functions
Inverse trigonometric formulas function as specialized rules in mathematics, aiding in the determination of angles and values through the application of inverse trigonometric functions. They are alternatively referred to as inverse trigonometric identities. These functions play a crucial role in determining angles when provided with specific ratios of sides within a right triangle.
Inverse Trigonometric Functions
If Sin θ = x, then θ = sin-1 x = arcsin(x)
Similarly,
θ = cos-1x = arccos(x)
θ = tan-1 x = arctan(x)
Also, the inverse properties could be defined as;
sin-1(sin θ) = θ
cos-1(cos θ) = θ
tan-1(tan θ) = θ
Inverse Trigonometry Formulas
Inverse Trigonometry Formulas are tools in math that let us find angles and values using inverse trigonometric functions, also known as reverse trigonometry functions.
- sin-1 (–x) = – sin-1 x
- cos-1 (–x) = π – cos-1 x
- tan-1 (–x) = – tan-1 x
- cosec-1 (–x) = – cosec-1 x
- sec-1 (–x) = π – sec-1 x
- cot-1 (–x) = π – cot-1 x
Degrees to Radians Formulas
If x is an angle in degrees and t is an angle in radians then:
π⁄180° = t⁄x ⇒ t = πx/180° and x = 180°t⁄x
Law of Sines Cosines and Tangents

Law of Sines
The Law of Sines relates the ratios of a triangle’s side lengths to the sines of its angles, stating that the sine of an angle divided by the length of the opposite side is constant for all angles in the triangle
sin α/a = sinβ/b = sin γ/c
Law of Cosines
The Law of Cosines is a trigonometric formula used to find the lengths of sides in non-right triangles, relating the square of a side to the sum of the squares of the other two sides minus twice the product of their lengths and the cosine of the included angle.
a² = b² + c² − 2bc cos α
b² = a² + c² − 2ac cos β
c² = a² + b² − 2ab cos γ
Law of Tangents
a − b/a + b = tan½(α − β)/tan½(α + β)
b – c/ b + c = tan½ (β − γ)/tan½(β + γ)
a – c/ a + c = tan½ (α − γ)/tan½(α + γ)
Trigonometry Formula Examples
Q1: What will be the value of sinAcosA if it is given that the value of sin2A is 1/2?
Sol: As we know that sin2A = 2sinAcosA
Given, sin2A = 1/2
Putting the value of sin2A on the LHS
2sinAcosA = 1/2
sinAcosA = (1/2) x (1/2)
Hence, sinAcosA = 1/4
Q2: It has been given that the value of sin2A is 1. Find out the value of (sinA – cosA).
Sol: Given, sin2A = 1
As we know, sin2A = 2sinAcosA
We have to find the value of sinA – cosA
On squaring (sinA – cosA), we get (sinA – cosA)2
sin2A + cos2A – 2sinAcosA
As sin2A + cos2A = 1
and 2sinAcosA = sin2A
Substituting these values in the above equation, we get => 1 – sin2A
As given sin2A = 1
=> 1-1 = 0
As, (sinA – cosA)2 = 0
sin A – cos A = √0
Hence, sinA – cosA = 0
Q3: In a right-angle triangle ABC with side AC as hypotenuse, the value of sin A is given to be 1/2. What will be the value of cos C.
Sol: Given ABC is a right-angled triangle.
AC is given to be hypotenuse, so, B must be the angle with value 90°.
Given, sinA = 1/2
As sin 30° = 1/2
So, sinA = sin30
Or, A = 30°
So, C must be 90° – 30° = 60°
Hence, cosC = cos60 = 1/2
So, the value of cosC = 1/2
Q4: Find the principal value of cos–1x, for x=√3/2.
Sol: If cos–1(√3/2) = θ, then cos θ = √3/2.
Since we are considering principal branch, θ ∈ [0 , π]. Also, since √3/2 > 0, θ being in the first quadrant, hence cos–1 (√3/2) = π/6.
|
314 videos|170 docs|185 tests
|
FAQs on Formulas: Trigonometry Formulas and Identities - Quantitative Aptitude for SSC CGL
| 1. What is the Pythagorean Identity in trigonometry? |  |
| 2. What are the basic trigonometric ratios? |  |
| 3. What are the reciprocal and quotient identities in trigonometry? |  |
| 4. What are the ranges of the trigonometric functions? |  |
| 5. What are the inverse trigonometry formulas and functions? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|





























