Fourier Series and it's Convergence | Calculus - Mathematics PDF Download
Fourier Series
Okay, in the previous two sections we’ve looked at Fourier sine and Fourier cosine series. It is now time to look at a Fourier series. With a Fourier series we are going to try to write a series representation for f(x) on −L≤x≤L in the form,
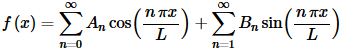
So, a Fourier series is, in some way a combination of the Fourier sine and Fourier cosine series. Also, like the Fourier sine/cosine series we’ll not worry about whether or not the series will actually converge to f(x) or not at this point. For now we’ll just assume that it will converge and we’ll discuss the convergence of the Fourier series in a later section.
Determining formulas for the coefficients, An and Bn, will be done in exactly the same manner as we did in the previous two sections. We will take advantage of the fact that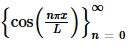 and
and 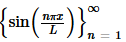 are mutually orthogonal on −L≤x≤L as we proved earlier. We’ll also need the following formulas that we derived when we proved the two sets were mutually orthogonal.
are mutually orthogonal on −L≤x≤L as we proved earlier. We’ll also need the following formulas that we derived when we proved the two sets were mutually orthogonal.
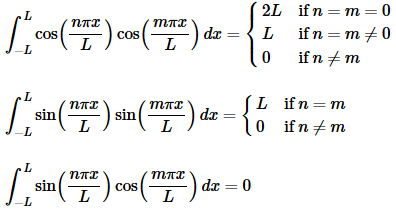
So, let’s start off by multiplying both sides of the series above by 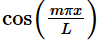 and integrating from –L to L. Doing this gives,
and integrating from –L to L. Doing this gives,
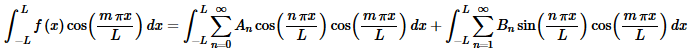
Now, just as we’ve been able to do in the last two sections we can interchange the integral and the summation. Doing this gives,
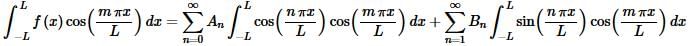
We can now take advantage of the fact that the sines and cosines are mutually orthogonal. The integral in the second series will always be zero and in the first series the integral will be zero if n≠m and so this reduces to,
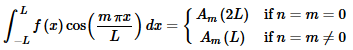
Solving for Am gives,
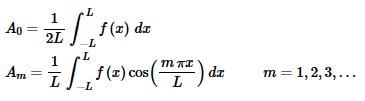
Now, do it all over again only this time multiply both sides by 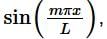 integrate both sides from –L to L and interchange the integral and summation to get,
integrate both sides from –L to L and interchange the integral and summation to get,
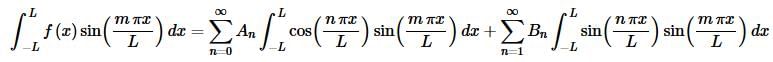
In this case the integral in the first series will always be zero and the second will be zero if n≠m and so we get,
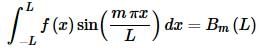
Finally, solving for Bm gives,
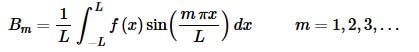
In the previous two sections we also took advantage of the fact that the integrand was even to give a second form of the coefficients in terms of an integral from 0 to L. However, in this case we don’t know anything about whether f(x) will be even, odd, or more likely neither even nor odd. Therefore, this is the only form of the coefficients for the Fourier series.
Before we start examples let’s remind ourselves of a couple of formulas that we’ll make heavy use of here in this section, as we’ve done in the previous two sections as well. Provided n in an integer then,
cos(nπ)=(−1)n sin(nπ)=0
In all of the work that we’ll be doing here n will be an integer and so we’ll use these without comment in the problems so be prepared for them.
Also, don’t forget that sine is an odd function, i.e. sin(−x)=−sin(x) and that cosine is an even function, i.e. cos(−x)=cos(x). We’ll also be making heavy use of these ideas without comment in many of the integral evaluations so be ready for these as well.
Now let’s take a look at an example.
Example 1 Find the Fourier series for f(x)=L−x on −L≤x≤L.
Solution:
So, let’s go ahead and just run through formulas for the coefficients.
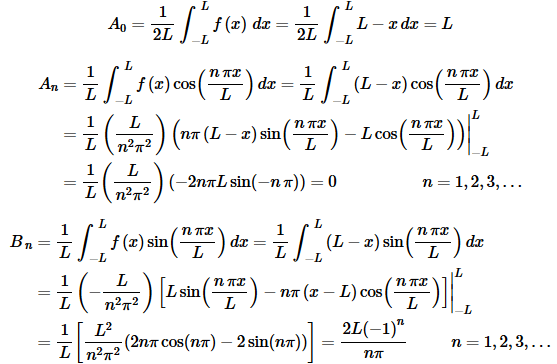
Note that in this case we had A0≠0 and An=0,n=1,2,3,… This will happen on occasion so don’t get excited about this kind of thing when it happens. The Fourier series is then,
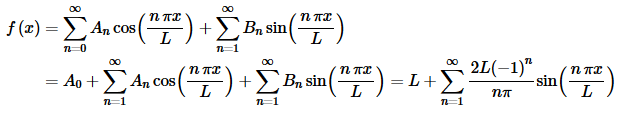
As we saw in the previous example sometimes we’ll get A0≠0 and An=0, n=1,2,3,... Whether or not this will happen will depend upon the function f(x) and often won’t happen, but when it does don’t get excited about it.
Let’s take a look at another problem.
Example 2 Find the Fourier series for 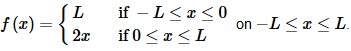
Solution:
Because of the piece-wise nature of the function the work for the coefficients is going to be a little unpleasant but let’s get on with it.
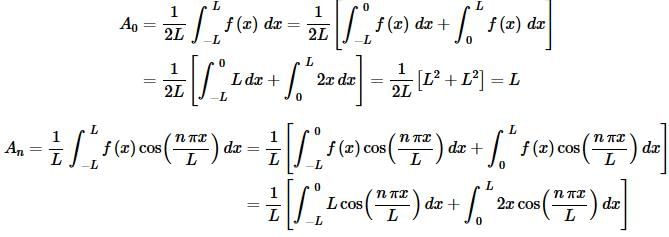
At this point it will probably be easier to do each of these individually.
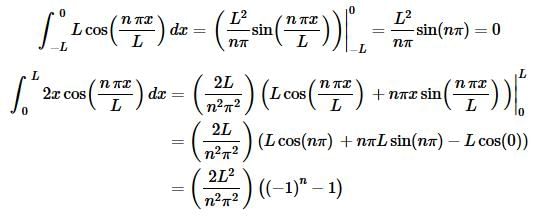
So, if we put all of this together we have,
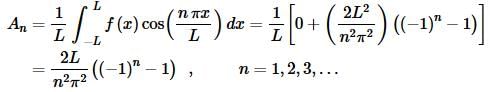
So, we’ve gotten the coefficients for the cosines taken care of and now we need to take care of the coefficients for the sines.
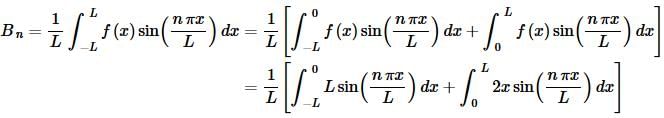
As with the coefficients for the cosines will probably be easier to do each of these individually.
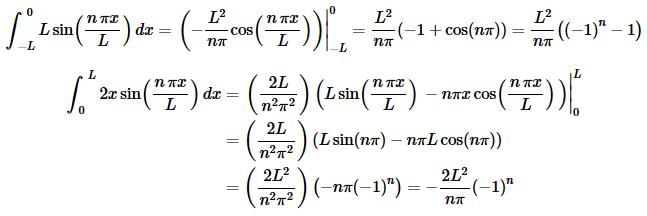
So, if we put all of this together we have,
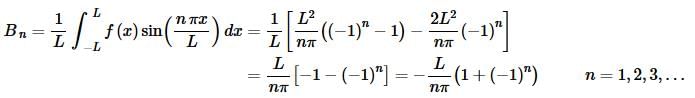
So, after all that work the Fourier series is,
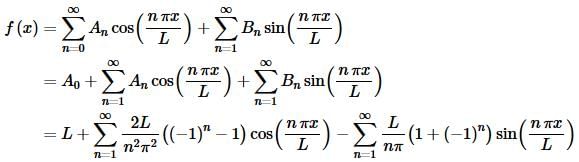
As we saw in the previous example there is often quite a bit of work involved in computing the integrals involved here.
The next couple of examples are here so we can make a nice observation about some Fourier series and their relation to Fourier sine/cosine series
Example 3 Find the Fourier series for f(x)=x on −L≤x≤L.
Solution:
Let’s start with the integrals for An.
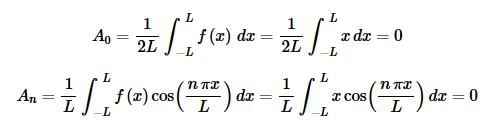
In both cases note that we are integrating an odd function (x is odd and cosine is even so the product is odd) over the interval [−L,L] and so we know that both of these integrals will be zero. Next here is the integral for Bn 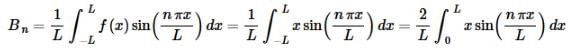
In this case we’re integrating an even function (x and sine are both odd so the product is even) on the interval [−L,L] and so we can “simplify” the integral as shown above. The reason for doing this here is not actually to simplify the integral however. It is instead done so that we can note that we did this integral back in the Fourier sine series section and so don’t need to redo it in this section. Using the previous result we get,
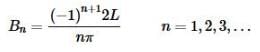
In this case the Fourier series is,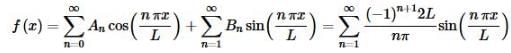
If you go back and take a look at Example 1 in the Fourier sine series section, the same example we used to get the integral out of, you will see that in that example we were finding the Fourier sine series for f(x)=x on −L≤x≤L. The important thing to note here is that the answer that we got in that example is identical to the answer we got here.
If you think about it however, this should not be too surprising. In both cases we were using an odd function on −L≤x≤L and because we know that we had an odd function the coefficients of the cosines in the Fourier series, An, will involve integrating and odd function over a symmetric interval, −L≤x≤L, and so will be zero. So, in these cases the Fourier sine series of an odd function on −L≤x≤L is really just a special case of a Fourier series.
Note however that when we moved over to doing the Fourier sine series of any function on 0≤x≤L we should no longer expect to get the same results. You can see this by comparing Example 1 above with Example 3 in the Fourier sine series section. In both examples we are finding the series for f(x)=x−Land yet got very different answers.
So, why did we get different answers in this case? Recall that when we find the Fourier sine series of a function on 0≤x≤L we are really finding the Fourier sine series of the odd extension of the function on −L≤x≤L and then just restricting the result down to 0≤x≤L. For a Fourier series we are actually using the whole function on −L≤x≤L instead of its odd extension. We should therefore not expect to get the same results since we are really using different functions (at least on part of the interval) in each case.
So, if the Fourier sine series of an odd function is just a special case of a Fourier series it makes some sense that the Fourier cosine series of an even function should also be a special case of a Fourier series. Let’s do a quick example to verify this.
Example 4 Find the Fourier series for f(x)=x2 on −L≤x≤L.
Solution:
Here are the integrals for the An and in this case because both the function and cosine are even we’ll be integrating an even function and so can “simplify” the integral.
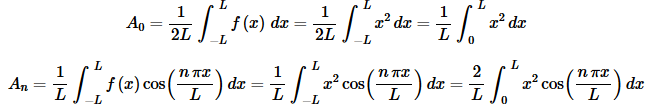
As with the previous example both of these integrals were done in Example 1 in the Fourier cosine series section and so we’ll not bother redoing them here. The coefficients are,
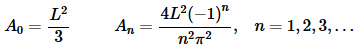
Next here is the integral for the Bn
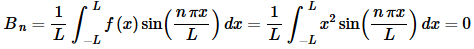
In this case the function is even and sine is odd so the product is odd and we’re integrating over −L≤x≤L and so the integral is zero.
The Fourier series is then,
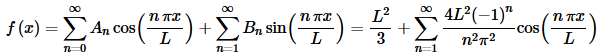
As suggested before we started this example the result here is identical to the result from Example 1 in the Fourier cosine series section and so we can see that the Fourier cosine series of an even function is just a special case a Fourier series.
Convergence of Fourier Series
Over the last few sections we’ve spent a fair amount of time to computing Fourier series, but we’ve avoided discussing the topic of convergence of the series. In other words, will the Fourier series converge to the function on the given interval?
In this section we’re going to address this issue as well as a couple of other issues about Fourier series. We’ll be giving a fair number of theorems in this section but are not going to be proving any of them. We’ll also not be doing a whole lot of in the way of examples in this section.
Before we get into the topic of convergence we need to first define a couple of terms that we’ll run into in the rest of the section. First, we say that f(x) has a jump discontinuity at x=a if the limit of the function from the left, denoted f(a−), and the limit of the function from the right, denoted f(a+), both exist and f(a−)≠f(a+).
Next, we say that f(x) is piecewise smooth if the function can be broken into distinct pieces and on each piece both the function and its derivative, f′(x), are continuous. A piecewise smooth function may not be continuous everywhere however the only discontinuities that are allowed are a finite number of jump discontinuities.
Let’s consider the function,
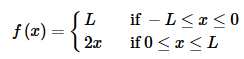
We found the Fourier series for this function in Example 2 of the previous section. Here is a sketch of this function on the interval on which it is defined, i.e. −L≤x≤L.
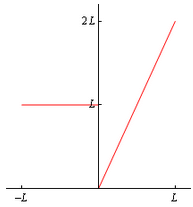
This function has a jump discontinuity at x=0 because f(0−)=L≠0=f(0+) and note that on the intervals −L≤x≤0 and 0≤x≤L both the function and its derivative are continuous. This is therefore an example of a piecewise smooth function. Note that the function itself is not continuous at x=0 but because this point of discontinuity is a jump discontinuity the function is still piecewise smooth.
The last term we need to define is that of periodic extension. Given a function, f(x), defined on some interval, we’ll be using −L≤x≤L exclusively here, the periodic extension of this function is the new function we get by taking the graph of the function on the given interval and then repeating that graph to the right and left of the graph of the original function on the given interval.
It is probably best to see an example of a periodic extension at this point to help make the words above a little clearer. Here is a sketch of the period extension of the function we looked at above,
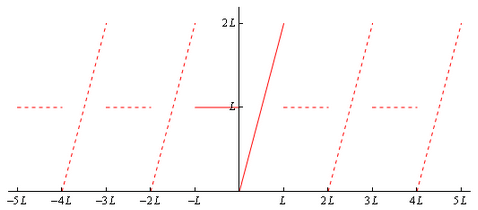
The original function is the solid line in the range −L≤x≤L. We then got the periodic extension of this by picking this piece up and copying it every interval of length 2L to the right and left of the original graph. This is shown with the two sets of dashed lines to either side of the original graph.
Note that the resulting function that we get from defining the periodic extension is in fact a new periodic function that is equal to the original function on −L≤x≤L.
With these definitions out of the way we can now proceed to talk a little bit about the convergence of Fourier series. We will start off with the convergence of a Fourier series and once we have that taken care of the convergence of Fourier Sine/Cosine series will follow as a direct consequence. Here then is the theorem giving the convergence of a Fourier series.
Convergence of Fourier series
Suppose f(x) is a piecewise smooth on the interval −L≤x≤L. The Fourier series of f(x) will then converge to,
- the periodic extension of f(x) if the periodic extension is continuous.
- the average of the two one-sided limits,
 if the periodic extension has a jump discontinuity at x=a.
if the periodic extension has a jump discontinuity at x=a.
The first thing to note about this is that on the interval −L≤x≤L both the function and the periodic extension are equal and so where the function is continuous on −L≤x≤L the periodic extension will also be continuous and hence at these points the Fourier series will in fact converge to the function. The only points in the interval −L≤x≤L where the Fourier series will not converge to the function is where the function has a jump discontinuity.
Let’s again consider Example 2 of the previous section. In that section we found that the Fourier series of,
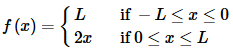
on −L≤x≤L to be,
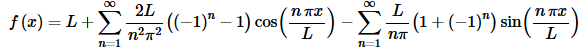
We now know that in the intervals −L<x<0 and 0<x<L the function and hence the periodic extension are both continuous and so on these two intervals the Fourier series will converge to the periodic extension and hence will converge to the function itself.
At the point x=0 the function has a jump discontinuity and so the periodic extension will also have a jump discontinuity at this point. That means that at x=0 the Fourier series will converge to,
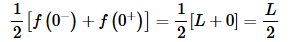
At the two endpoints of the interval, x=−L and x=L, we can see from the sketch of the periodic extension above that the periodic extension has a jump discontinuity here and so the Fourier series will not converge to the function there but instead the averages of the limits.
So, at x=−L the Fourier series will converge to,
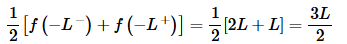
and at x=L the Fourier series will converge to,
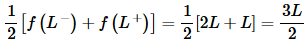
Now that we have addressed the convergence of a Fourier series we can briefly turn our attention to the convergence of Fourier sine/cosine series. First, as noted in the previous section the Fourier sine series of an odd function on −L≤x≤L and the Fourier cosine series of an even function on −L≤x≤L are both just special cases of a Fourier series we now know that both of these will have the same convergence as a Fourier series.
Next, if we look at the Fourier sine series of any function, g(x), on 0≤x≤L then we know that this is just the Fourier series of the odd extension of g(x) restricted down to the interval 0≤x≤L. Therefore, we know that the Fourier series will converge to the odd extension on −L≤x≤L where it is continuous and the average of the limits where the odd extension has a jump discontinuity. However, on 0≤x≤L we know that g(x) and the odd extension are equal and so we can again see that the Fourier sine series will have the same convergence as the Fourier series.
Likewise, we can go through a similar argument for the Fourier cosine series using even extensions to see that Fourier cosine series for a function on 0≤x≤L will also have the same convergence as a Fourier series.
The next topic that we want to briefly discuss here is when will a Fourier series be continuous. From the theorem on the convergence of Fourier series we know that where the function is continuous the Fourier series will converge to the function and hence be continuous at these points. The only places where the Fourier series may not be continuous is if there is a jump discontinuity on the interval −L≤x≤L and potentially at the endpoints as we saw that the periodic extension may introduce a jump discontinuity there.
So, if we’re going to want the Fourier series to be continuous everywhere we’ll need to make sure that the function does not have any discontinuities in −L≤x≤L. Also, in order to avoid having the periodic extension introduce a jump discontinuity we’ll need to require that f(−L)=f(L). By doing this the two ends of the graph will match up when we form the periodic extension and hence we will avoid a jump discontinuity at the end points.
Here is a summary of these ideas for a Fourier series.
Suppose f(x) is a piecewise smooth on the interval −L≤x≤L. The Fourier series of f(x) will be continuous and will converge to f(x) on −L≤x≤L provided f(x) is continuous on −L≤x≤L and f(−L)=f(L).
Now, how can we use this to get similar statements about Fourier sine/cosine series on 0≤x≤L? Let’s start with a Fourier cosine series. The first thing that we do is form the even extension of f(x) on −L≤x≤L. For the purposes of this discussion let’s call the even extension g(x) As we saw when we sketched several even extensions in the Fourier cosine series section that in order for the sketch to be the even extension of the function we must have both,
If one or both of these aren’t true then g(x) will not be an even extension off(x).
So, in forming the even extension we do not introduce any jump discontinuities at x=0 and we get for free that g(−L)=g(L). If we now apply the above theorem to the even extension we see that the Fourier series of the even extension is continuous on −L≤x≤L. However, because the even extension and the function itself are the same on 0≤x≤L then the Fourier cosine series of f(x) must also be continuous on 0≤x≤L.
Here is a summary of this discussion for the Fourier cosine series.
Suppose f(x) is a piecewise smooth on the interval 0≤x≤L. The Fourier cosine series of f(x) will be continuous and will converge to f(x) on 0≤x≤L provided f(x) is continuous on 0≤x≤L.
Note that we don’t need any requirements on the end points here because they are trivially satisfied when we convert over to the even extension.
For a Fourier sine series we need to be a little more careful. Again, the first thing that we need to do is form the odd extension on −L≤x≤L and let’s call it g(x). We know that in order for it to be the odd extension then we know that at all points in −L≤x≤L it must satisfy g(−x)=−g(x) and that is what can lead to problems.
As we saw in the Fourier sine series section it is very easy to introduce a jump discontinuity at x=0 when we form the odd extension. In fact, the only way to avoid forming a jump discontinuity at this point is to require that f(0)=0.
Next, the requirement that at the endpoints we must have g(−L)=−g(L) will practically guarantee that we’ll introduce a jump discontinuity here as well when we form the odd extension. Again, the only way to avoid doing this is to require f(L)=0.
So, with these two requirements we will get an odd extension that is continuous and so we know that the Fourier series of the odd extension on −L≤x≤L will be continuous and hence the Fourier sine series will be continuous on 0≤x≤L. Here is a summary of all this for the Fourier sine series.
Suppose f(x) is a piecewise smooth on the interval 0≤x≤L. The Fourier sine series of f(x) will be continuous and will converge to f(x) on 0≤x≤L provided f(x) is continuous on 0≤x≤L, f(0)=0 and f(L)=0.
The next topic of discussion here is differentiation and integration of Fourier series. In particular, we want to know if we can differentiate a Fourier series term by term and have the result be the Fourier series of the derivative of the function. Likewise, we want to know if we can integrate a Fourier series term by term and arrive at the Fourier series of the integral of the function.
Note that we’ll not be doing much discussion of the details here. All we’re really going to be doing is giving the theorems that govern the ideas here so that we can say we’ve given them.
Let’s start off with the theorem for term by term differentiation of a Fourier series.
Given a function f(x) if the derivative, f′(x), is piecewise smooth and the Fourier series of f(x) is continuous then the Fourier series can be differentiated term by term. The result of the differentiation is the Fourier series of the derivative, f′(x).
One of the main condition of this theorem is that the Fourier series be continuous and from above we also know the conditions on the function that will give this. So, if we add this into the theorem to get this form of the theorem,
Suppose f(x) is a continuous function, its derivative f′(x) is piecewise smooth and f(−L)=f(L) then the Fourier series of the function can be differentiated term by term and the result is the Fourier series of the derivative.
For Fourier cosine/sine series the basic theorem is the same as for Fourier series. All that’s required is that the Fourier cosine/sine series be continuous and then you can differentiate term by term. The theorems that we’ll give here will merge the conditions for the Fourier cosine/sine series to be continuous into the theorem.
Let’s start with the Fourier cosine series.
Suppose f(x) is a continuous function and its derivative f′(x) is piecewise smooth then the Fourier cosine series of the function can be differentiated term by term and the result is the Fourier sine series of the derivative.
Next the theorem for Fourier sine series.
Suppose f(x) is a continuous function, its derivative f′(x) is piecewise smooth, f(0)=0 and f(L)=0 then the Fourier sine series of the function can be differentiated term by term and the result is the Fourier cosine series of the derivative.
The theorem for integration of Fourier series term by term is simple so there it is.
Suppose f(x) is piecewise smooth then the Fourier sine series of the function can be integrated term by term and the result is a convergent infinite series that will converge to the integral of f(x).
Note however that the new series that results from term by term integration may not be the Fourier series for the integral of the function.
|
112 videos|65 docs|3 tests
|

|
Explore Courses for Mathematics exam
|

|

















