Fourier Series | Basic Physics for IIT JAM PDF Download
Consider a periodic function f(x) with a period L and let us calculate the Fourier transform of it. We define a new function f0(x)=f(x) in the [0, L] interval and zero otherwise. Then: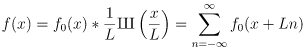
Apply Fourier transform: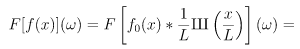
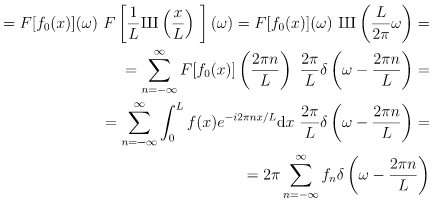
where fn are called Fourier coefficients: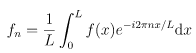
We can see that the Fourier transform is zero for  . For
. For 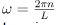 it is equal to a delta function times a 2π multiple of a Fourier series coefficient. The delta functions structure is given by the period L of the function f(x). All the information that is stored in the answer is inside the fn coefficients, so those are the only ones that we need to calculate and store.
it is equal to a delta function times a 2π multiple of a Fourier series coefficient. The delta functions structure is given by the period L of the function f(x). All the information that is stored in the answer is inside the fn coefficients, so those are the only ones that we need to calculate and store.
The function f(x) is calculated from the fn coefficients by applying the inverse Fourier transform to the final result of as follows: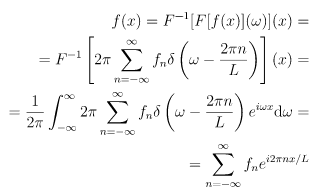
The expansion is called a Fourier series. It is given by the Fourier coefficients fn. The equation provides the relation between a Fourier transform and a Fourier series.
For example for f(x) = sin(x), the only nonzero Fourier coefficients for L=2π are f-1 = i/2 and f1 =-i/2 . The Fourier transform then is: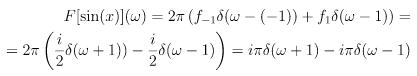
For f(x) = 1 the only nonzero Fourier coefficient is f0=1, the Fourier transform then is: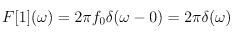
For f(x) = e3ix the only nonzero Fourier coefficient for L=2π is f3= 1, the Fourier transform then is: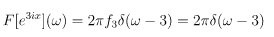
For 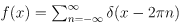 the Fourier coefficients for L=2\pi are all equal to fn = 1/2π and the Fourier transform is:
the Fourier coefficients for L=2\pi are all equal to fn = 1/2π and the Fourier transform is: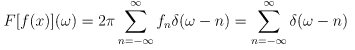
Note: if we start from, for simplicity on an interval [-π,π]: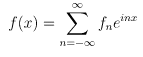
To calculate the Fourier coefficients fn, we can just multiply both sides of by e-imx and integrate: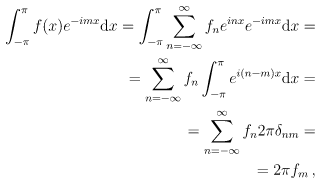
so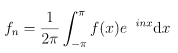
|
210 videos|156 docs|94 tests
|
FAQs on Fourier Series - Basic Physics for IIT JAM
| 1. What is a Fourier series? |  |
| 2. How is a Fourier series used in physics? |  |
| 3. What are the applications of Fourier series in physics? |  |
| 4. What are the limitations of Fourier series? |  |
| 5. Can Fourier series be applied to non-periodic functions? |  |

|
Explore Courses for Physics exam
|

|

















