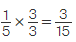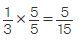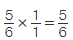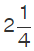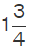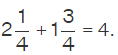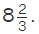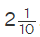Fractions and Operations | Mathematics for JAMB PDF Download

A fraction shows part of a whole. This whole can be a region or a collection. The word fraction is derived from the Latin word "fractio" which means 'to break'. The Egyptians, being the earliest civilization to study fractions, used fractions to resolve their mathematical problems, which included the division of food, supplies, and the absence of a bullion currency.
In Ancient Rome, fractions were only written using words to describe a part of the whole. In India, the fractions were first written with one number above another (numerator and denominator), but without a line. It was the Arabs only, who added the line which is used to separate the numerator and the denominator.

What are Fractions?

In Mathematics, fractions are represented as a numerical value, which defines a part of a whole. A fraction can be a portion or section of any quantity out of a whole, where the whole can be any number, a specific value, or a thing. Let us understand this concept using an example. The following figure shows a pizza that is divided into 8 equal parts. Now, if we want to express one selected part of the pizza, we can express it as 1/8 which shows that out of 8 equal parts, we are referring to 1 part.
It means one in eight equal parts. It can also be read as:

• One-eighth, or
• 1 by 8

If we select 2 parts of the pizza, it will be expressed as 2/8. Similarly, if we are referring to 6 parts of this pizza, we would write it as 6/8 as a fraction.

Parts of a Fraction

All fractions consist of a numerator and a denominator and they are separated by a horizontal bar known as the fractional bar.

• The denominator indicates the number of parts in which the whole has been divided into. It is placed in the lower part of the fraction below the fractional bar.
• The numerator indicates how many sections of the fraction are represented or selected. It is placed in the upper part of the fraction above the fractional bar.

Types of Fractions 

Based on the numerator and denominator, which are parts of a fraction, there are different types of fractions as listed below:

Proper Fraction

Proper fractions are the fractions in which the numerator is less than its denominator. For example, 5/7, 3/8, 2/5, and so on are proper fractions.

Improper Fraction 
An improper fraction is the type of fraction in which the numerator is more than or equal to its denominator. It is always the same or greater than the whole. For example, 4/3, 5/2, 8/5, and so on.

Unit Fraction 
Fractions in which the numerator is 1 are known as unit fractions. For example, 1/4, 1/7, 1/9, and so on.

Mixed Fraction 
A mixed fraction is a mixture of a whole number and a proper fraction. For example, 5¹/₃, where 5 is the whole number and 1/3 is the proper fraction, or, 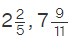  and so on. 

Equivalent Fraction

Equivalent fractions are the fractions that represent the same value after they are simplified. To get equivalent fractions of any given fraction:

• We can multiply both the numerator and the denominator of the given fraction by the same number.
• We can divide both the numerator and the denominator of the given fraction by the same number.

Example: Find the two fractions that are equivalent to 5/7.
Solution: Equivalent Fraction 1: Let us multiply the numerator and the denominator with the same number 2. This means, 5/7= (5 × 2)/(7 × 2) = 10/14
Equivalent Fraction 2: Let us multiply the numerator and the denominator with the same number 3. This means, 5/7 = (5 × 3)/(7 × 3) = 15/21
Therefore, 10/14, 15/21, and 5/7 are equivalent fractions.

Like and Unlike Fractions

Like fractions are the fractions that have the same denominators. For example, 5/15, 3/15, 17/15, and 31/15 are like fractions.
Unlike fractions are the fractions which have different denominators. For example, 2/7, 9/11, 3/13, and 39/46 are unlike fractions.

Fraction on a Number Line

The representation of fractions on a number line demonstrates the intervals between two integers, which also shows us the fundamental principle of fractional number creation. The fractions on a number line can be represented by making equal parts of a whole, i.e., from 0 to 1. The denominator of the fraction would represent the number of equal parts in which the number line will be divided and marked.
For example, if we need to represent 1/8 on the number line, we need to mark 0 and 1 on the two ends and divide the number line into 8 equal parts. Then, the first interval can be marked as 1/8. Similarly, the next interval can be marked as 2/8, the next one can be marked as 3/8, and so on. It should be noted that the last interval represents 8/8 which means 1. Observe the following number line that represents these fractions on a number line.

Addition and Subtraction of Fractions

While adding and subtracting fractions, we need to check whether the fractions have the same denominators or different denominators and then the calculation starts. Let us learn more about the addition and subtraction of fractions in this article.

How to Add and Subtract Fractions?

Addition and subtraction of fractions is done using similar rules in which the denominators are checked before the addition or subtraction starts. After the denominators are checked, we can add or subtract the given fractions accordingly. The denominators are checked in the following way.

• If the denominators of the given fractions are the same, we add or subtract only the numerators and we retain the denominator.
• If the denominators are different, we convert the fractions to like fractions so that the denominators become the same, and then we add or subtract, whatever is required.

Adding and Subtracting Fractions with Like Denominators

The process for adding and subtracting fractions with like denominators is quite simple because we just need to work with the numerators.

Adding Fractions with Like Denominators

Let us add the fractions 1/5 and 2/5 using rectangular models. In this case, both the fractions have the same denominators. These fractions are called like fractions. The following figure represents both the fractions in the same model.

• 1/5 indicates that 1 out of 5 parts are shaded yellow.
• 2/5 indicates that 2 out of 5 parts are shaded blue.

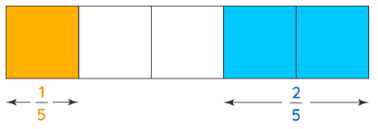
Out of the 5 parts, 3 parts are shaded. In the fractional form, this can be represented as 3/5. Now, let us add the fractions with like denominators in numerical terms. In this case, we need to add 1/5 + 2/5. Let us use the following steps to understand the addition.

• Step 1: Add the numerators of the given fractions. Here, the numerators are 1 and 2, so it will be 1 + 2 = 3
• Step 2: Retain the same denominator. Here, the denominator is 5.
• Step 3: Therefore, the sum of 1/5 + 2/5 = (1 + 2)/5 = 3/5

It should be noted that we use the same method for subtracting fractions.

Subtracting Fractions with Like Denominators

Let us subtract the fractions 2/5 and 1/5 using rectangular models. We will represent 2/5 in this model by shading 2 out of 5 parts. We will further shade out 1 part from our shaded parts of the model which would represent removing 1/5.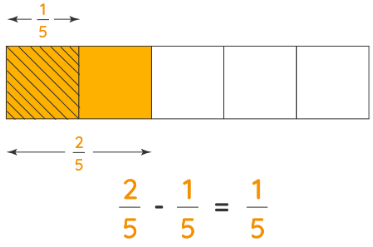

We are now left with 1 part in the shaded parts of the model. Now, let us subtract the fractions with like denominators in numerical terms. In this case, we need to subtract 2/5 - 1/5. Let us understand the procedure using the following steps.

• Step 1: We will subtract the numerators of the given fractions. Here, the numerators are 2 and 1, so it will be 2 - 1 = 1
• Step 2: Retain the same denominator. Here, the denominator is 5.
• Step 3: Therefore, the difference of 2/5 - 1/5 = (2 - 1)/5 = 1/5

Adding and Subtracting Fractions with Unlike Denominators

For adding and subtracting fractions with unlike denominators, we need to convert the unlike fractions to like fractions by writing their equivalent fractions in such a way that their denominators become the same. Let us understand this with the help of an example.
Example: Add 1/5 + 1/3
Solution: For adding unlike fractions we need to use the following steps

• Step 1: Find the Least Common Multiple (LCM) of the denominators. Here, the LCM of 5 and 3 is 15.
• Step 2: Convert the given fractions to like fractions by writing the equivalent fractions for the respective fractions such that their denominators remain the same. Here, it will be
• Step 3: Similarly, an equivalent fraction of 1/3 with denominator 15 is 
• Step 4: Now, that we have converted the given fractions to like fractions we can add the numerators and retain the same denominator. This will be 3/15 + 5/15 = 8/15

Subtracting Fractions with Unlike Denominators

For subtracting unlike fractions, we follow the same steps as we did for the addition of unlike fractions. Let us understand this with the help of an example.
Example: Subtract 5/6 - 1/3 

• Step 1: Find the Least Common Multiple (LCM) of the denominators. Here, the LCM of 6 and 3 is 6.
• Step 2: Convert the given fractions to like fractions by writing the equivalent fractions for the respective fractions such that their denominators remain the same. Here, it will be
• Step 3: Similarly, an equivalent fraction of 1/3 with denominator 6 is 1/3 × 2/2 × 2/6
• Step 4: Now, that we have converted the given fractions to like fractions we can subtract the numerators and retain the same denominator. This will be 5/6 - 2/6 = 3/6. This can be further reduced to 1/2

Adding and Subtracting Mixed Fractions

Adding and subtracting mixed fractions is done by converting the mixed fractions to improper fractions and then the addition or subtraction is done as per the requirement. Let us understand these with the help of the following example.
Example: Add the mixed fractions:
Solution: First let us convert the mixed fractions to improper fractions.

• Step 1: Convert the given mixed fractions to improper fractions. So,   will become 9/4; and 
  
•  will become 7/4 
• Step 2: Add the fractions by adding the numerators because the denominators are the same. This will be 9/4 + 7/4= 16/4.
• Step 3: Reduce the fraction, if required. This will become, 16/4 = 4. Therefore,

Adding and Subtracting Fractions with Whole Numbers

Adding and subtracting fractions with whole numbers can be done using the following method. Let us understand this using an example.
Example: Add 7/4 + 5
Solution: Let us add 7/4 + 5 using the following steps.

Step 1: Write the whole number in the form of a fraction. In this case the whole number is 5 which can be written as 5/1. So, now we need to add 7/4 + 5/1

Step 2: Now, find the LCM of the denominators and convert the given fractions to like fractions. Here the LCM of 4 and 1 is 4. And after converting them to like fractions we get, (7 × 1)/(4 × 1) + (5 × 4)/(1 × 4) = 7/4 + 20/4

Step 3: Add the numerators while the denominator remains the same. Here, 7/4 + 20/4 = 27/4 =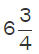
Important Notes on Adding and Subtracting Fractions

• For adding and subtracting like fractions, we can directly work with the numerators while the denominators remain the same.
• For adding and subtracting unlike fractions, never add or subtract the numerators and denominators directly. Convert them to like fractions and then add or subtract.

Multiplying Fractions

Multiplying fractions starts with the multiplication of the given numerators, followed by the multiplication of the denominators. Then, the resultant fraction is simplified further and reduced to its lowest terms, if needed. Learn all about multiplying fractions in this article.

How to Multiply Fractions?

The multiplication of fractions is not like the addition or subtraction of fractions, where the denominator should be the same. Here, any two fractions with different denominators can easily be multiplied. The only thing to be kept in mind is that the fractions should not be in the mixed form, they should either be proper fractions or improper fractions. Let us learn how to multiply fractions through the following steps:

• Step 1: Multiply the numerators.
• Step 2: Multiply the denominators.
• Step 3: Reduce the resultant fraction to its lowest terms.

Let us understand these steps with the help of an example.
Example: Multiply the following fractions: 1/3 × 3/5.
Solution: We start by multiplying the numerators: 1 × 3 = 3, then, multiply the denominators: 3 × 5 = 15. This can be written as: (1 × 3)/(3 × 5) = 3/15. Now, reduce this value to its lowest form. 3 is the Greatest Common Factor (GCF) of 3 and 15, so, divide both 3 and 15 by 3 to simplify the fraction. Therefore, 1/3 × 3/5 = 1/5.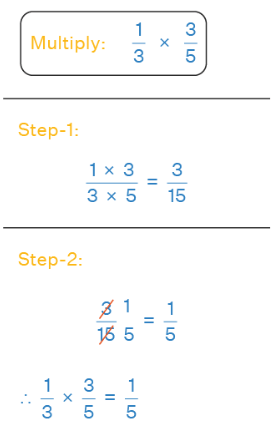

Rules of Multiplying Fractions

While multiplying fractions, the following rules should be kept in mind:

• Rule 1: The first rule is to convert mixed fractions to improper fractions if any. Then, multiply the numerators of the given fractions.
• Rule 2: Multiply the denominators separately.
• Rule 3: Simplify the value obtained to its lowest term.

These three rules can be applied to any two fractions to find their product. Now, let us learn the individual cases of multiplying fractions with different types of fractions.

Multiplying Fractions with Same Denominator

Multiplying fractions with the same denominator does not change the rule of multiplication of fractions. Fractions that have the same denominator are termed like fractions. Although addition and subtraction of like fractions are different from the addition and subtraction of unlike fractions, in the case of multiplication and division the method remains the same. We multiply the numerators, then the denominators, and then the fraction is reduced to its lowest terms.
Example: Multiply 1/3 × 5/3
Solution: We can multiply these fractions using the following steps.

• Step 1: Multiply the numerators, 1 × 5 = 5.
• Step 2: Multiply the denominators, 3 × 3 = 9.
• Step 3: The product that we get is 5/9. This cannot be reduced any further, therefore 5/9 is the answer.

Multiplying Fractions with Different Denominators

Multiplying fractions with unlike denominators is exactly the same as the multiplication of like fractions. Let us understand this with an example.
Example: Multiply 4/12 × 16/24.

We can multiply these fractions using the following steps:

Step 1: Multiply the numerators, 4 × 16 = 64.

Step 2: Multiply the denominators, 12 × 24 = 288.

Step 3: The product that we get is 64/288. This can be reduced to 2/9. Therefore, 2/9 is the answer.

Alternative Method 
The same fractions can be multiplied using another method in which we simplify the fractions among themselves and then multiply the numerators, then the denominators to get the final product.

Example: Multiply 4/12 × 16/24.
Let us multiply the given fractions using the following steps:

• Step 1: We will simplify the given fractions among themselves. In other words, these fractions can be reduced to 1/3 × 2/3.
• Step 2: Let us multiply the numerators, 1 × 2 = 2.
• Step 3: Now, let us multiply the denominators, 3 × 3 = 9.
• Step 4: Therefore, the product that we get is 2/9.

Multiplying Fractions with Whole Numbers

Multiplying fractions by whole numbers is an easy concept. As we know that multiplication is the repeated addition of the same number, this fact can be applied to fractions as well.
Multiplying Fractions with Whole Numbers Visual Model 
Let us consider this example: 4 × 2/3. This means 2/3 is added 4 times. Let us represent this example using a visual model. Four times two-thirds is represented as: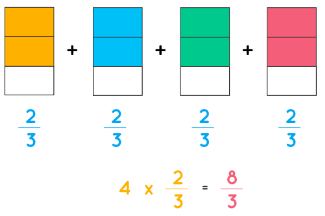

Steps of Multiplying Fractions with Whole Numbers 
In order to multiply fractions with whole numbers, we use the simple rule of multiplying the numerators, then multiplying the denominators, and then reducing them to the lowest terms. However, in the case of whole numbers, we write them in the fractional form by placing '1' in the denominator. Let us understand this with an example.
Example: Multiply: 5 × 3/4.
Solution: Let us use the following steps to multiply the given fraction with a whole number.

• Step 1: Here, 5 is a whole number that can be written as 5/1, and then it can be multiplied as we multiply regular fractions.
• Step 2: This means, we need to multiply 5/1 × 3/4.
• Step 3: Multiply the numerators, 5 × 3 = 15.
• Step 4: Multiply the denominators, 1 × 4 = 4.
• Step 5: The resultant product is 15/4 which cannot be reduced further.
• Step 6: Since 15/4 is an improper fraction, we will change it to a mixed fraction, 15/4 =

Multiplying Fractions with Mixed Numbers

Mixed numbers or mixed fractions are fractions that consist of a whole number and a proper fraction, like 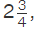where 2 is the whole number and 3/4 is the proper fraction. For multiplying mixed fractions, we need to change the mixed fractions into an improper fraction before multiplying. For example, if the number iswe need to change this to 8/3. Let us understand this with the help of an example.
Example: Multiply 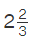and
Solution: The following steps can be used to multiply fractions with mixed numbers.

• Step 1: Change the given mixed fractions to improper fractions, i.e., (8/3) × (13/4).
• Step 2: Multiply the numerators of the improper fractions, and then multiply the denominators. This will give 104/12.
• Step 3: Now, reduce the resultant fraction to its lowest terms, which will make it 26/3.
• Step 4: Further, convert the answer back to a mixed fraction which will be

Multiplication of Improper Fractions

Now let us understand the multiplication of improper fractions. We already know that an improper fraction is one where the numerator is bigger than the denominator. When multiplying two improper fractions, we frequently end up with an improper fraction. For example, to multiply 3/2 × 7/5 which are two improper fractions, we need to take the following steps:

• Step 1: Multiply the numerators and denominators. (3 × 7)/(2 × 5) = 21/10.
• Step 2: The fraction 21/10 cannot be reduced further to its lowest terms.
• Step 3: Hence, the answer is 21/10 which can be written as

Division of Fractions

Division means sharing an item equally. We have learned about the division of whole numbers, now let us see how to divide fractions. A fraction has two parts - a numerator and a denominator. Dividing fractions is almost the same as multiplying them. For the division of fractions, we multiply the first fraction by the reciprocal (inverse) of the second fraction. Let us learn more about the division of fractions in this article.

How to Divide Fractions?

We know that division is a method of sharing equally and putting into equal groups. We divide a whole number by the divisor to get the quotient. Now, when we do division of a fraction by another fraction, it is the same as multiplying the fraction by the reciprocal of the second fraction. The reciprocal of a fraction is a simple way of interchanging the fraction's numerator and denominator. Observe the following figure to learn a simple rule of dividing fractions.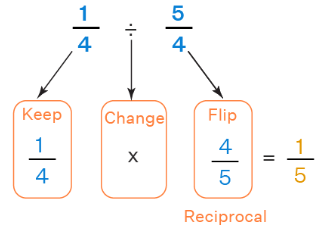

In the subsequent sections, we will learn the division of fractions with fractions, whole numbers, decimals, and mixed numbers. In every case, we will be using the same rule of dividing fractions as given above. 

Dividing Fractions by Fractions

We just learned how to divide fractions by taking the reciprocal. Now, let us see the method of dividing fractions by fractions with an example. Have a look at the formula of the division of a fraction by fraction given below. If x/y is divided by a/b, this implies,
x/y ÷ a/b
⇒ x/y × b/a (reciprocal of a/b is b/a)
⇒ xb/ya
Now, if we need to divide: 5/8 ÷ 15/16, we will substitute the values of the given numerators and denominators.
5/8 ÷ 15/16 = 5/8 × 16/15 = 2/3
∴ The value of 5/8 ÷ 15/16 = 2/3.

Division of Fractions with Whole Numbers

For the division of fractions with whole numbers, we need to multiply the denominator of the given fraction with the given whole number. In the general form, if x/y is the fraction and a is the whole number, then x/y ÷ a = x/y × 1/a = x/ya.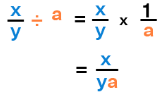

Let us take an example and divide 2/3 with 4.
2/3 ÷ 4 = 2/3 × 1/4
= 1/6
Therefore, 2/3 ÷ 4 gives us 1/6. This is how we divide fractions with whole numbers.

Dividing Fractions with Decimals

We know that decimal numbers themselves are a fraction to base 10. We can represent the decimal in the fractional form and then perform the division. For dividing fractions with decimals, follow the steps given below:

• Convert the given decimal to a fraction.
• Divide both the fractions.

Consider the example, 4/5 ÷ 0.5. Here, 0.5 can be written in fractional form as 5/10 or 1/2. Now, divide 4/5 by 1/2. This implies, 4/5 ÷ 1/2 = 4/5 × 2/1 = 8/5. This is how we perform the division of fractions with decimals. Now let us learn how to divide fractions with mixed numbers.

Division of Fractions and Mixed Numbers

We have learned how to convert mixed fractions to improper fractions. For the division of fractions with mixed numbers, we have to convert the mixed fraction to an improper fraction first and then divide them as we divide two fractions. Consider the following example.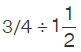

So, the first step is to convert 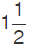to an improper fraction. 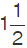is the same as 3/2. Now, it can be solved in the following way:
3/4 ÷ 3/2
⇒ 3/4 × 2/3
⇒ 6/12 = 1/2
Therefore, 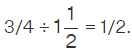If you want to divide a mixed number with a fraction, first convert the mixed number to an improper fraction and follow the same steps as shown above.