Free & Forced Vibration | Theory of Machines (TOM) - Mechanical Engineering PDF Download

Mechanical Vibrations

The to and for motion of a body about its mean position is termed as mechanical vibrations or harmonic vibrations or oscillations.
[Mean Position = Equilibrium Position = Zero Position] All are same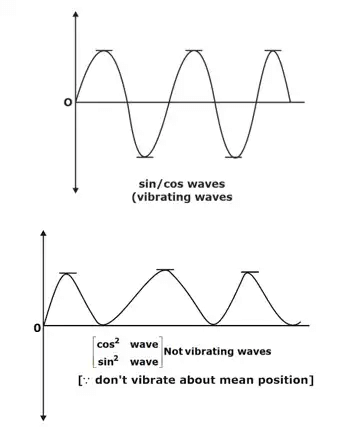
Type of oscillating waves

Any vibrating system is a combination of:

• E storing device (i.e. mass = m)
• E storing device (having stiffness = s)
• Kinetic friction
• Unbalanced forces

1. Natural Vibrations
   The vibrations in which there is no friction at all (static friction may have, but no kinetic friction) as well as there is no unbalanced force after the initial release of the system are called as “Natural Vibrations”
   Spring-mass systemUsing D-Alembert's Principle:
   ma + sx = 0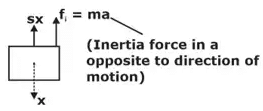
   
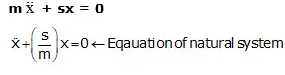
2. Energy Method to Calculate Natural Frequency
   This method is used only for natural vibrations and is used specially for Rolling problems.
   In Natural Vibrations,
   As, kinetic friction = 0
   Total energy = constant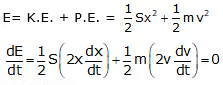
   
3. Torsional Vibrations
   The vibrations of a system about its own center of mass is termed as torsional vibrations.
   In case of torsional vibrations, At fixed Print, as. Hence, Vibration’s amplitude will also zero. This point is called ‘Node’.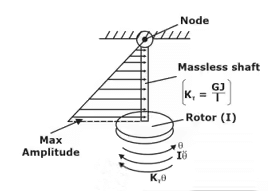
   shaft-rotor system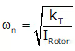
   (k_T = Torsional stiffness of shaft)
   Note: If shaft mass MOI is also considered (= I_s)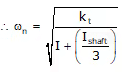
   
   (i) Two-Rotor System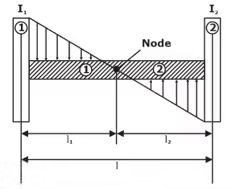
   2-rotor systemAt Node Point:
   ω_n1 = ω_n2 (i.e. net vibrations of Node Point = 0)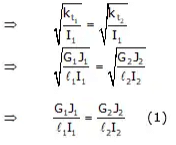
   
   for this same shaft, G₁J₁ = G₂ J₂      [∵ G₁ = G₂, J₁ = J₂]
   ⇒ I₁ℓ₁ = I₂ℓ₂    (2)
   Also, ℓ₁ + ℓ₂ = ℓ   (3)
4. Rayleigh’s Method to Calculate Natural Frequency (Method of Static Deflection of Mass)
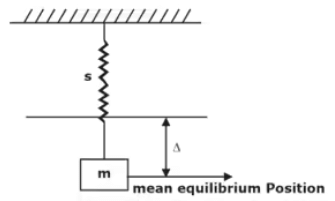   Basic spring Mass System∇ = static deflection of mass ′m′
   = (mg/s)  [∵ mg = s · ∇]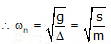
   
5. Longitudinal-Vibrations of Beams
   Vibrations along the length of Beam are termed as longitudinal vibrations.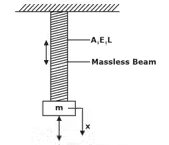
   longitudinal vibrations of a beamAxial or longitudinal stiffness of beam,
   s = (AE/L)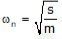
   
6. Transverse –Vibrations of Beams
   Vibrations in a direction perpendicular to axis of the Beam.
   Transverse vibrations of a beam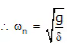
   where, δ = static defection of Beam Under transverses loads
   Example:
   For a cantilever Beam with Point load 'w' at free end δ = WL³/ 3EL