Function & Its types | Engineering Mathematics - Civil Engineering (CE) PDF Download

Functions in Mathematics

A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets; mapping from A to B will be a function only when every element in set A has one end, only one image in set B.
Example: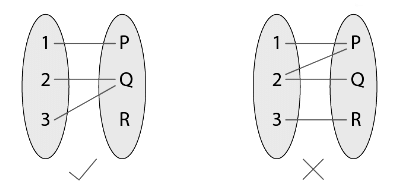

Another definition of functions is that it is a relation “f” in which each element of set “A” is mapped with only one element belonging to set “B”. Also in a function, there can’t be two pairs with the same first element.

A Condition for a Function

Set A and Set B should be non-empty.
In a function, a particular input is given to get a particular output. So, A function f: A->B denotes that f is a function from A to B, where A is a domain and B is a co-domain.
For an element, a, which belongs to A, a ∈ A, a unique element b, b ∈ B is there such that (a,b) ∈ f.

The unique element b to which f relates a, is denoted by f(a) and is called f of a, or the value of f at a, or the image of a under f.

• The range of f (image of a under f)
• It is the set of all values of f(x) taken together.
• Range of f = { y ∈ Y | y = f (x), for some x in X}

A real-valued function has either P or any one of its subsets as its range. Further, if its domain is also either P or a subset of P, it is called a real function.

Vertical Line Test
Vertical line test is used to determine whether a curve is a  function or not. If any curve cuts a vertical line at more than one points then the curve is not a function.

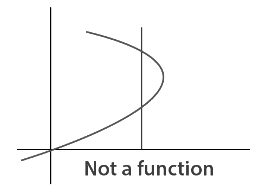
Representation of Functions

Functions are generally represented as f(x).
Let , f(x) = x³.
It is said as f of x is equal to x cube.
Functions can also be represented by g(), t(),… etc.

Steps for Solving Functions

Question: Find the output of the function g(t) = 6t² + 5 at
(i) t = 0
(ii) t = 2

The given function is g(t) = 6t² + 5
(i) At t = 0, g(0) = 6(0)² + 5 = 5
(ii) At t = 2, g(2) = 6(2)² + 5 = 29

Types of Functions

1. Injective (One-to-One) Functions: A function in which one element of Domain Set is connected to one element of Co-Domain Set.

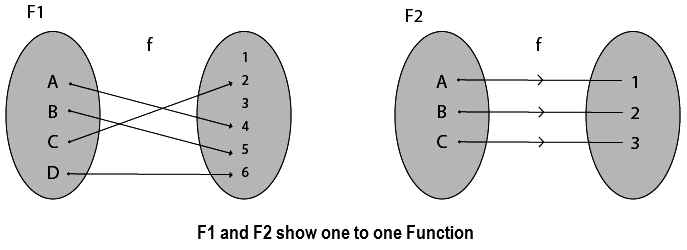
2. Surjective (Onto) Functions: A function in which every element of Co-Domain Set has one pre-image.
Example: Consider, A = {1, 2, 3, 4}, B = {a, b, c} and f = {(1, b), (2, a), (3, c), (4, c)}.
It is a Surjective Function, as every element of B is the image of some A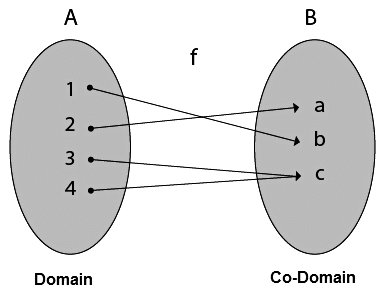

3. Bijective (One-to-One Onto) Functions: A function which is both injective (one to - one) and surjective (onto) is called bijective (One-to-One Onto) Function.

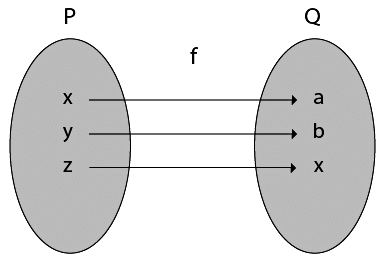
Example:

Consider P = {x, y, z}  

         Q = {a, b, c}  

and f: P → Q such that  

         f = {(x, a), (y, b), (z, c)}  

The f is a one-to-one function and also it is onto. So it is a bijective function.

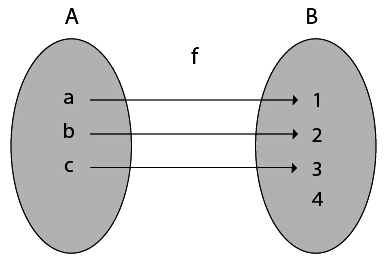
4. Into Functions: A function in which there must be an element of co-domain Y does not have a pre-image in domain X.

Example:

Consider, A = {a, b, c}  

          B = {1, 2, 3, 4}   and f: A → B such that  

          f = {(a, 1), (b, 2), (c, 3)}  

In the function f, the range i.e., {1, 2, 3} ≠ co-domain of Y i.e., {1, 2, 3, 4}  

Therefore, it is an into function

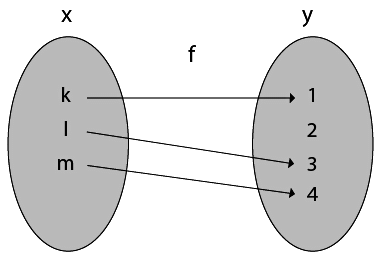
5. One-One Into Functions: Let f: X → Y. The function f is called one-one into function if different elements of X have different unique images of Y.
Example:

Consider, X = {k, l, m}  

          Y = {1, 2, 3, 4} and f: X → Y such that  

          f = {(k, 1), (l, 3), (m, 4)}  

The function f is a one-one into function

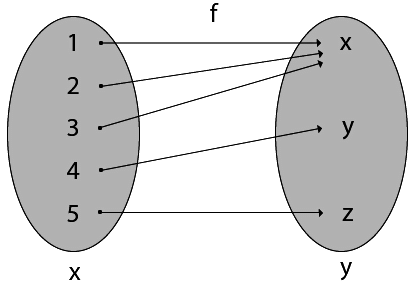
6. Many-One Functions: Let f: X → Y. The function f is said to be many-one functions if there exist two or more than two different elements in X having the same image in Y.
Example:

Consider X = {1, 2, 3, 4, 5}  

         Y = {x, y, z} and f: X → Y such that  

         f = {(1, x), (2, x), (3, x), (4, y), (5, z)}  

The function f is a many-one function

7. Many-One Into Functions: Let f: X → Y. The function f is called the many-one function if and only if is both many one and into function.
Example:

Consider X = {a, b, c}  

         Y = {1, 2} and f: X → Y such that  

         f = {(a, 1), (b, 1), (c, 1)}  

As the function f is a many-one and into, so it is a many-one into function.

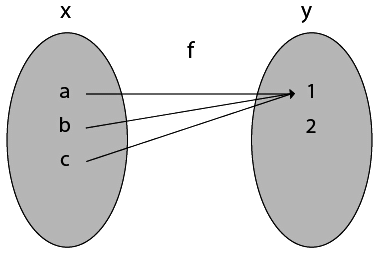
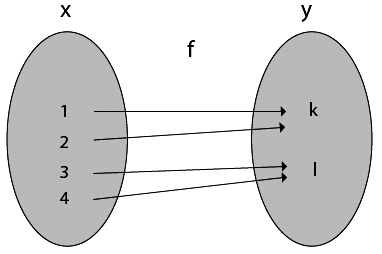
8. Many-One Onto Functions: Let f: X → Y. The function f is called many-one onto function if and only if is both many one and onto.
Example:

Consider X = {1, 2, 3, 4}  

         Y = {k, l} and f: X → Y such that  

         f = {(1, k), (2, k), (3, l), (4, l)}  

The function f is a many-one (as the two elements have the same image in Y) and it is onto (as every element of Y is the image of some element X). So, it is many-one onto function