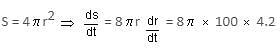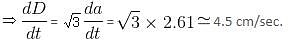This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Functions (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Functions - 2
Try yourself:If f f(-x) = 2x, what is the value of f(2)?
f(-x) = 2x, what is the value of f(2)?
Explanation
Putting x = 1/2,
We get f(2) + 2f(-1/2) = 1
Or, f(2) = 1 - 2f(-1/2)........(i)
Putting x = -2,
We get f(-1/2) - (1/2)f(2) = -4
Or, f(-1/2) = -4 + (1/2)f(2).........(ii)
Putting (ii) in (i),
We get f(2) = 1 - 2 (-4 + (1/2)f(2))
Or, f(2) = 1 + 8 - f(2)
Or, 2f(2) = 9
Or, f(2) = 9/2 = 4.5
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:Let f(x) = 7x3 + 23x + 18. If the value of f(x + 8) - f(x + 7) - f(x + 6) + f(x + 5) - f(x + 4) + f(x + 3) + f(x + 2) - f(x + 1) is a constant, then find that value.
Explanation
If the answer is a constant, this implies that the answer does not depend on the variable i.e. x.
Thus, if we take only constant terms that we would get after writing all the functions, we will get the required answer.
Thus, 7(83 - 73 - 63 + 53 - 43 + 33 + 23 - 13) + 18(1 - 1 - 1 + 1 - 1 + 1 + 1 - 1) + 23(8 - 7 - 6 + 5 - 4 + 3 + 2 - 1) = 336.
Hence, option d is correct.
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:Let f(x) = x5 + ax4 + bx3 + cx2 + dx + e and f(1) = f(2) = f(3) = f(4) = f(5). Then a is equal to
Explanation
Let A be the common value of f(1), f(2), f(3), f(4), and f(5).
Then f(x) - A has the roots 1, 2, 3, 4, and 5.
Since f(x) - A = x5 + ax4 + bx3 + cx2 + dx + (e - A), f(x) - A is a polynomial of degree 5 and, hence, the five numbers 1, 2, 3, 4, and 5 must be the five roots of f(x).
It follows that the sum of the roots of f(x) is 1 + 2 + 3 + 4 + 5 = 15.
Since in general the sum of the n roots of a polynomial anxn + an - 1xn - 1 + …….. + a1x + a0 of degree n is , we get that the sum of the roots of f(x) - A is - a.
, we get that the sum of the roots of f(x) - A is - a.
Thus, - a = 15 so that a = - 15.
(Comment: When we say that in general the sum of the n roots above is , we mean that the polynomial may have "multiple" roots and we are to count the roots with multiplicity. For example, (x - 1)2 (x - 2)3 = x5 - 8x4 + …. Where 8 represents the sum of the roots counting 1 twice and 2 thrice.)
, we mean that the polynomial may have "multiple" roots and we are to count the roots with multiplicity. For example, (x - 1)2 (x - 2)3 = x5 - 8x4 + …. Where 8 represents the sum of the roots counting 1 twice and 2 thrice.)
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:If f(x) = (x5 - 1) (x3 + 1), g(x) = (x2 - 1) (x2 - x + 1) and h(x) is a polynomial such that f(x) = g(x)h(x), what is the value of h(1)?
Explanation
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:Consider a recursive function C defined by:
C(n, 0) = n + 1
C(0, i) = C(1, i - 1) for i > 0
C(n, i) = C(C(n -1, i), ( i - 1)) for n > 0 and i > 0
Compute C(1, 2) from the above definition.
Explanation
C(n, 0) = n + 1 ……….. (1)
C(0, i) = C(1, i - 1) ……….. (2)
C(n, i) = C(C (n - 1, i), (i - 1)) ……….. (3)
From (3), put n = 1 and i = 2
C(1, 2) = C[C(0, 2), 1] ……….. (4)
From (2),
C(0, 2) = C(1, 1) ……….. (5)
From (3) and (5),
C(1, 1) = C[C(0, 1), 0] ……….. (6)
Now, C(0, 1) = C(1, 0) [From (2)]
Also, C(1, 0) = 1 + 1 = 2 [From (1)]
Put this in (6)
C(1, 1) = C(2, 0) = 2 + 1 = 3 [From (1)]
Put this value in (5)
C(0, 2) = 3
Put this value in (4)
C(1, 2) = C(3, 1) ……….. (7)
Now, from (3),
C(3, 1) = C[C(2, 1), 0] ……….. (8)
C(2, 1) = C[C(1, 1), 0]
= C(3, 0) = 4
Put in (8)
C(3, 1) = C(4, 0) = 5 ………. (9)
From (7) to (9),
C(1, 2) = 5.
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:Let f and g be functions and f(g(x)) = x + 2 and f(s) =  . What is the value of g(t)?
. What is the value of g(t)?
Explanation
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:Let f(x) = 1 -  Find f(f(f(…f(4)..))), when there are 1997 f's in the composition.
Find f(f(f(…f(4)..))), when there are 1997 f's in the composition.
Explanation
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:The value of the function f(n) is 35/16 which is represented as f(n) =  Find the value of x(Answer upto one decimal place).
Find the value of x(Answer upto one decimal place).
Explanation
f(n) = 1 + 4x + 7x2 + 10x3 + …..(1)
xf(n) = x + 4x2 + 7x3 + 10x4 + ……∝ …(2)
Subtracting (1) and (2), we get
(1 - x) f(n) = 1 + 3x + 3x2 + 3x3 +......
⇒ (1 - x) f(n) = 1 + 3x/1-x
⇒ (1 - x) × 35 x 16 = 1 + 2x/1 - x
⇒ 35(1 - x)2 = 16 + 32x
⇒ 35x2 - 102x + 19 = 0
⇒ (7x - 19)(5x - 1) = 0
x ≠ 19/7 (∴ For infinity series, common ratio < 1)
∴ x = 1/5
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:If f(x + y) = f(x) + f(y) and f(1) + f(2) + f(3) … f(10) = 1, find the value of f(1).
Explanation
Given: f(x + y) = f(x) + f(y)
f(1 + 1) = f(2) = f(1) + f(1) = 2f(1)
f(2 + 1) = f(3) = f(2) + f(1) = 3f(1)
Similarly, f(4) = 4f(1), f(5) = 5f(1) … f(10) = 10f(1)
Given expression:
f(1) + f(2) + f(3) … f(10) = 1
f(1) + 2f(1) + 3f(1) + ... + 10f(1) = 1
f(1)(1 + 2 + 3 + ... + 10) = 1
f(1) = 1/55
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:If f is a function such that f(0) = 2, f(1) = 3 and f(x + 2) = 2f(x) - f(x + 1), then f(5) is equal to
Explanation
f(x + 2) = 2f(x) - f(x + 1) ... (i)
Put x = 0 in (i),
f(2) = 2f(0) - f(1) = 2 × 2 - 3 = 1
Put x = 1 in (i),
f(3) = 2f(1) - f(2) = 2 × 3 - 1 = 5
Put x = 2 in (i),
f(4) = 2f(2) - f(3) = 2 × 1 - 5 = -3
Put x = 3 in (i),
f(5) = 2f(3) - f(4) = 2 × 5 - (-3) = 13
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:If the graph of y = f(x) is transformed to the graph of 2y - 6 = -4f(x - 3), point (a, b) on the graph of y = f(x) becomes point (A, B) on the graph of 2y - 6 = -4f(x - 3), where A and B are given by:
Explanation
y = f(x) is transformed to the graph of 2y - 6 = -4f(x - 3).
(A, B) = ?
2y - 6 = -4f(x - 3)
2y = -4f(x - 3) + 6
y = -2f(x - 3) + 3
The graph of y = -2f(x - 3) + 3 is that of y = f(x) shifted 3 units to the right, stretched vertically by a factor of 2, reflected on the x-axis and shifted up by 3 units. A point of y = f(x) will undergo the same transformation. Hence, point (a, b) on the graph of y = f(x) becomes:
(a + 3, b) on the graph of y = f(x - 3) (shifted 3 units to the right)
(a + 3, 2b) on the graph of y = 2f(x - 3) (stretched vertically by 2)
(a + 3, -2b) on the graph of y = -2f(x - 3) (reflected on the x-axis)
(a + 3, -2b + 3) on the graph of y = -2f(x - 3) + 3 (shifted up 3 units)
Report a problem
Question for Practice Questions Level 2: Functions - 2
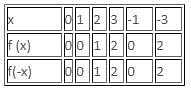
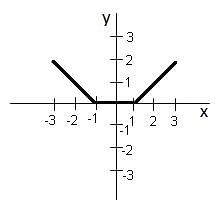
Try yourself:Given below is a graph made up of line segments shown as thick lines. Which of the following options is correct?

Explanation
The following table shows the values of the graph of the functions f(x) and f(-x) at different values of x:

From the above table, we get
f(x) = f(-x)
f(x) - f(-x) = 0
Report a problem
Question for Practice Questions Level 2: Functions - 2
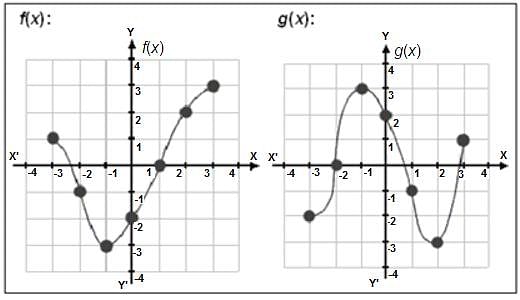
Try yourself:The graphs of f(x) and g(x) are shown below:

Find (fog)(-1).
Explanation
First note that (fog)(-1) = f(g(- 1)).
This means that you first need to find g(-1).
So, look at the graph of g(x) and find x = -1.
Tracing up to the graph of g(x), you get x = -1, y = 3, i.e. the point (-1, 3) is on the graph of g(x).
So, g(-1) = 3. Now, plug this value into f(x).
To do this, look at the graph of f(x) and find x = 3.
Tracing up to the graph of f(x), you will get x = 3, y = 3, i.e. the point (3, 3) is on the graph of f(x).
So, f(3) = 3. Then, (fog)(-1) = f(g(- 1)) = f(3) = 3
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:A sphere's radius is increasing at the rate of 4.2 cm/sec. Find the rate at which its area of surface changes when the radius is 100 cm.
Explanation

= 10,560 cm2/s
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:A cube's edge is changing at the rate of 2.61 cm/sec. The rate of change of its longest diagonal will be (approx.)
Explanation
Longest diagonal of a cube = D = √3 a, where a is the length of each side.

Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:A large company intends to maximise its profits using calculus. Its unit sales price is Rs. 500 and cost of production = 100 + 5X2, where X is the total units sold or produced. Find the most profitable production level.
Explanation
Profit = P = Total SP - Total CP
= 500 X - (100 + 5X2) = - 5X2 + 500X - 100
Here, X = Production level
dP/dX = 0
500 - 10X = 0 X = 50 units
The most profitable production level is 50 units.
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:A company sells its products at Rs. 155 per kg and its cost of manufacture is given by Rs. (X2 + 5) per kg. Find the production level for maximum profit, if X = production level.
Explanation
Let X kg be the most profitable level.
⇒ Profit = P = Total SP - Total CP = 155X - (X2 + 5) x ⇒ dP/dX = 0 ⇒ 155 - 3X2 - 5 = 0
⇒ x = √50 kg
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:In Indore, Annapurna area has 2000 telephone subscribers and government collects fixed charges of Rs. 280 per month from each subscriber. The government proposes to increase the tariff and if it is forecasted for each rupee increase, there will be an equivalent amount of subscribers discontinuing. So, what increase will bring maximum revenue to the government?
Explanation
F(x) = (2000 - x)(280 + x)
F`(x) = (2000 - x) + (280 + x)(-1)
= 2000 - x - 280 - x = 1720 - 2x
F"(x) = -2 (which is negative)
So,
1720 - 2x = 0
1720 = 2x
x = 860
x = Rs. 860
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:The maximum area of a rectangle with perimeter equal to 12 units will be
Explanation
Area will be maximum if it is a square of edge = 12/4 = 3 or area = 32 = 9 sq. units.
Report a problem
Question for Practice Questions Level 2: Functions - 2
Try yourself:Let f1(n) = n - 28 n 6
f2(m) = m - 16 ≤ m - 1
f(x) = f(m) + f(n)
What is the value of fmax(x) and fmin(x)?
Explanation
Put m = 0 and n = 0, the least value of f(x) = n - 28 + m - 16 = - 28 + (- 16) = - 44 and the greatest value of f(x) = 6 - 1 = 5.
Report a problem
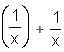 f(-x) = 2x, what is the value of f(2)?
f(-x) = 2x, what is the value of f(2)?
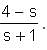 . What is the value of g(t)?
. What is the value of g(t)?
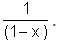 Find f(f(f(…f(4)..))), when there are 1997 f's in the composition.
Find f(f(f(…f(4)..))), when there are 1997 f's in the composition.
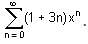 Find the value of x(Answer upto one decimal place).
Find the value of x(Answer upto one decimal place).


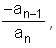 , we get that the sum of the roots of f(x) - A is - a.
, we get that the sum of the roots of f(x) - A is - a.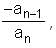 , we mean that the polynomial may have "multiple" roots and we are to count the roots with multiplicity. For example, (x - 1)2 (x - 2)3 = x5 - 8x4 + …. Where 8 represents the sum of the roots counting 1 twice and 2 thrice.)
, we mean that the polynomial may have "multiple" roots and we are to count the roots with multiplicity. For example, (x - 1)2 (x - 2)3 = x5 - 8x4 + …. Where 8 represents the sum of the roots counting 1 twice and 2 thrice.)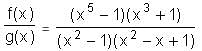
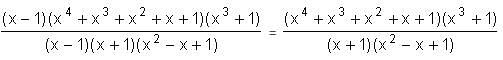
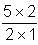 = 5.
= 5.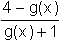
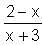
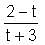
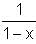
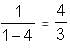
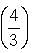 = 1 -
= 1 -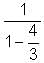 = 4.
= 4.