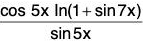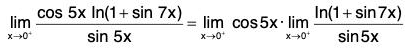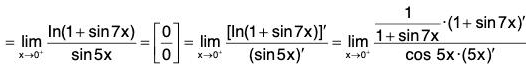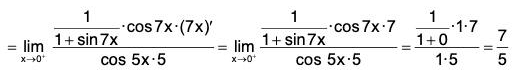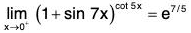Functions of One Variable - II | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Rolle's Theorem : Statement |

|
| Mean Value Theorem |

|
| Taylor's Theorem |

|
| MAXIMA AND MINIMA OF ONE VARIABLE |

|
| Indeterminate forms and L'Hospital's Rule |

|
Rolle's Theorem : Statement
If a function f defined on [a, b] is such that it is :
[R1] continuous in the closed interval [a, b]
[R2] differentiable in the open interval (a, b)
and [R3] f(a) = f(b),
then there exists atleast one point c ∈ (a, b) such that f’(c) = 0.
Proof : Since f is continuous in the closed interval [a, b], therefore by the property of continuity f will be bounded and will attain bounds in [a, b].
Let m and M be the infimum and supremum of f in [a, b], then there exist c and d in [a, b] such that f(c) = M and f(d) = m
Case 1 : When M = m, then
f(x) = M = m, ∀ x ∈ [a, b]
⇒ f’(x) = 0, ∀ x ∈ [a, b]
⇒ f’(c) = 0, where c ∈ (a, b)
Thus the theorem hold good at any point c of (a, b).
Case 2 : When M ≠ m, then by R3, f(a) = f(b), and atleast one of the numbers M and m be different from f(a) and f(b) i.e.,
M = f(c) ≠ f(a), f(b)
⇒ c ≠ a, b ⇒ c ∈ (a, b)
Since the function f is differentiable in (a, b), then the derivative exist at a point c.
Therefore RHD and LHD are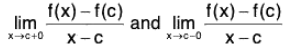
both exist and each equal to f(c).
Since f(c) is the maximum value of f(x) in (a,b),
∴ f(c + h) < f(c) and f(c - h) < f(c) ...(1)
Now 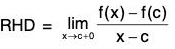
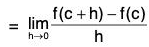 [Putting x = c + h]
[Putting x = c + h]
≤ 0 [∵ by(1) f(c + h) - f(c) < 0]
and 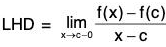
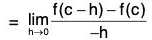 [Putting x = c - h]
[Putting x = c - h]
≥ 0 [∵ by(1) f(c - h) - f(c) < 0]
Thus both the derivatives are of opposite signs.
Therefore both these derivatives will be equal only when f(c) = 0.
Geometrical Interpretation of Rolle’s Theorem
Statement : It a curve has a tangent at every point there of and the ordinates of its extremities A and B are equal i.e. f(a) = f(b); then there exists atleast one point P of the curve other than A and B, the tangent at which is parallel to x-axis.
Case 1 : When f(x) = k (constant),
Then the graph of this function will be a straight line parallel to the x-axis whose equation is y = k and the derivative
f’(x) = 0, ∀ x ∈ [a, b]
Case 2 : When f(x) ≠ k (constant),
Then the graph of this function is a continuous curve of the following type in [a, b] as shown below: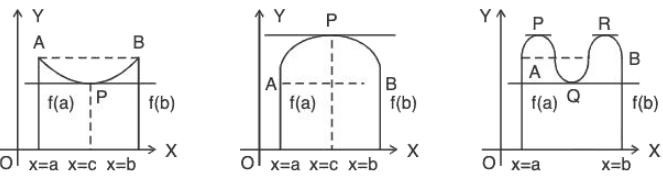
From these figures it is quite intuitively that there must be atleast one point P(x = c) (may be more) of the curve other than A and B, the tangent at which is parallel to x-axis and at these points f’(c) = 0.
Case of Failure : The theorem will not hold good if any of the three conditions fails to hold good i.e.,
- the function f is discontinuous at x = c.
- the derivative does not exist at x = c.
- f(a) ≠ f(b).
The following figures will illustrate these cases of failure:

Algebraic interpretation of Rolle’s theorem:
Statement : If f(x) be a polynomial in x and x = a and x = b are any two roots of the equation f(x) = 0, then there exists at least one root of the equation f’(x) = 0, which lies between a and b.
Remarks : The Rolle’s theorem is not applicable for those functions which do not satisfy even one condition of Roll’s theorem.
Another useful form of Rolle’s Theorem:
If a function f defined on [a, a + h] is such that it is:
[R1] continuous in [a, a + h],
[R2] differentiable in (a, a + h) and
[R3] f(a) = f(a + h),
then ∃ θ ∈ (0, 1) such that f (a + θh) = 0.
Example: Verify Rolle’s theorem for the function in the interval mentioned against:
f(x) = x(x + 3)e-x/2, x ∈ [-3, 0]
R1. Since the given function x(x + 3), x is a polynomial of x, therefore it is continuous for every value of x and e-x/2 is also continuous for every value of x.
Therefore their product is also continuous for every value of x
Hence the function is continuous, particularly in [-3, 0].
R2. f(x ) = (2x + 3) e-x/2 + x(x + 3) • e-x/2(-1/2) = (1/2)e-x/2 (6 + x - x2)
which is not infinite or indeterminate at any point of (-3, 0).
Thus f(x) is differentiable in (-3, 0).
R3. f(-3) = 0 = f(0)
Thus the given function f satisfies all the three conditions of Roll’s theorem.
Hence Verified.
Therefore there must be atleast one point c in (-3, 0), where
Since e-c/2 is not zero for any finite value c, therefore 6 + c - c2 = 0 ⇒ c = - 2, 3
One value of c = -2 ∈ (-3, 0) Hence Verified.
Example: Verify Rolle’s Theorem for 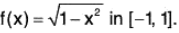
The given function being an algebraic function of x is continuous in [- 1, 1].
Now
So f(x) is derivable in ] - 1, 1[. Also f(1) = f(-1) = 0.
Thus f(x) satisfies all the conditions of Rolle’s Theorem.
So there exists a point c ∈ ] - 1, 1[ such that f'(c) = 0
Clearly f’(c) = 0 for c = 0 ∈ ] - 1, 1[.
Hence the given function satisfies the hypothesis and the conclusion of Rolle’s Theorem.
Example: Examine the validity of the hypotheses and the conclusion of Rolle’s theorem for the function f(x) = 1 - (x - 1)2/3 on [0, 2].
The given function, being an algebraic function of x is continuous in [0, 2].
Now
⇒ f’(x) does not exist at x = 1 ⇒ f is not derivable at x = 1
⇒ f is not derivable in ]0, 2[.
But f(0) = f(2) = 0.
Hence f does not satisfy all the conditions of Rolle’s theorem. Clearly, the conclusion of Rolle’s theorem is not valid for the given function.
Example: Show that between any two roots of ex cos x = 1, there exists at least one root of ex sin x - 1 = 0.
Let α and β be any two distinct roots of ex cos x = 1. ...(1)
∴ eα cos α = 1 and eβ cos β = 1.
Define a function f as follows :
f(x) = e-x - cos x, ∀ x ∈ [α, β]. ...(2)
Obviously f is continuous in [α, β] and f is derivable in ]α, β[.
Indeed, f’(x) = - e-x + sin x ∀ x ∈ ]α, β[.
From (2),
Similarly, f(β) = 0 and so f(α) = f(β).
Thus f satisfies all the conditions of Rolle's Theorem in [α, β] and so there exists some γ ∈ ]α, β[ such that f(γ) = 0.
⇒ sin γ - e-γ = 0 ⇒ eγ sin γ - 1 = 0, α < γ < β.
Hence γ is a root of ex sin x - 1 = 0, α < γ < β.
Example: Prove that between any two real roots of ex sin x = x, there is at least one root of cos x + sin x = e-x.
Let x = α, x = β be any two distinct roots of ex sin x = x.
∴ eα sin α = α and eβ sin β = β. ...(1)
Define a function f on [α, β] as follows :
f(x) = ex sin x - x ∀ x ∈ [α, β]. ...(2)
Clearly, (i) f continuous in [α, β], (ii) f is derivable in ]α, β[ and f(α) = 0 = f(β),. by (1). Hence by Rolle’s theorem, there exists some γ ∈ ]α, β[ i.e.,α < γ < β such that f’(γ) = 0. ...(3)
From (2), f’(x) = ex sin x + ex cos x - 1
⇒ f’(g) = eγ (sin γ + cos γ) - 1
∴ eγ (sin γ + cos γ) - 1 = 0, using (3)
or sin γ + cos γ = 1/eγ = e-γ, α < γ < β.
Hence γ is a root of sin x + cos x = e-x, where α < γ < β.
Example: If p(x) is polynomial and k ∈ R, prove that between any two real roots of p(x) = 0, there is a roots of p’(x) + k p(x) = 0.
Let f(x) = ekx p(x), x ∈ R. ...(1)
Let α and β be any two real roots of p(x), where α < β. Then p(α) = 0 = p(β) f(α) = 0 = f(β), by (1).
Obviously, (i) f is continuous in [α, β], (ii) f is derivable in ]α, β[ and (iii) f(α) = f(β). Hence, by Rolle’s theorem, there exists some γ ∈ ]α, β[ such that f’(γ) = 0.
From (1), f(x) = k ekx p(x) + ekx p’(x) = ekx [p’ (x) + kp (x)].
∴ 0 = f (γ) = ekγ [p' (γ) + k p (γ)]
⇒ p’(γ) + k p(γ) = 0, as ekγ ≠ 0.
Hence γ is a root of p’(x) + kp (x) = 0, where α < γ < β.
Mean Value Theorem
Lagrange’s Mean Value Theorem
Statement : If a function f with domain [a, b] is such that it is
[L1] continuous in [a, b], and
[L2] differentiable in (a, b),
then ∃ c ∈ (a, b) such that: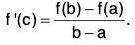
Proof : Let us define a new function φ with domain [a, b] involving the given function f(x) as follows :
φ(x) = f(x) + Ax ...(1)
where A is a constant to be determined such that φ(a) = φ(b) ...(2)
⇒ f(a) + Aa = f(b) + Ab
⇒ 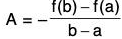 ...(3)
...(3)
We observe that the function φ is also defined on [a, b] and is the sum of two continuous functions on [a, b] and differentiable in (a, b), therefore φ is :
R1. φ,[a, b] is continuous in [a, b]
R2. φ,(a, b) is differentiable in (a, b)
and R3. φ,(a) = φ,(b) [by the condition of constant]
Thus φ satisfies all the three conditions of Rolle’s theorem, therefore accordingly, there must be atleast one point c in (a, b) such that
φ'(c) = 0
⇒ f'(c) + A = 0 ⇒ f ’(c) = - A
⇒  a < c < b [by (3)]
a < c < b [by (3)]
Important Particular Case : If f(a) = f(b), then it reduces to Rolle’s theorem.
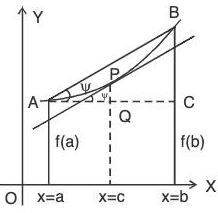
Geometrical Interpretation of Lagrange’s MV Theorem:
If a curve y = f(x) is continuous between two given points whose abscissae are x = a and x = b respectively and a tangent can be drawn to the curve at every point, then there exists atleast one point x = c, c ∈ (a, b) such that the tangent there at is parallel to the chord joining the two given end points.
Let the arc APB represents the graph of the function y = f(x) and a and b be the ordinates of A and B respectively. Join AB. Draw perpendiculars from A and B on x-axis. Let the chord AB makes an angle ψ with the x-axis, then from the right angled triangle ACB,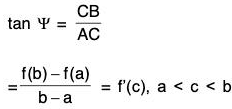
Another Useful Form
Statement : A function f defined on [a, a + h] is such that it is :
- Continuous in [a, a + h];
- Differentiable in (a, a + h)
then ∃ θ ∈ (0, 1) such that :
f(a + h) - f(a) = h f' (a + θh).
If we put b - a = h or b = a + h in Lagrange’s MV theorem, then any point c can be taken as c = a + θ h between a and b, where 0 < θ < 1.
Therefore by Lagrange MVT, we have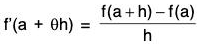
⇒ f(a + h) - f(a) = h f(a + θh), 0 < θ < 1.
Important Deduction from Lagrange’s MV Theorem :
Theorem : If a function f is
- continuous in [a, b]
- differentiable in (a, b), ∀ x ∈ (a, b), then
(a) f’(x) = 0 ⇒ f is a constant function in (a, b).
(b) f’(x) > 0 ⇒ f is strictly increasing in [a, b].
(c) f’(x) < 0 ⇒ f is strictly decreasing in [a, b].
If the derivatives of two functions at every point of the interval (a, b) is same, then the functions differ by a constant.
Example: Verify Lagrange’s Mean Value Theorem for the function f(x) = 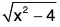 in [2, 4].
in [2, 4].
The function f(x) =
s an algebraic function of x, so f is continuous in [2, 4]. Also f is derivable in ]2, 4[.
Now
Since f satisfies all the conditions of Lagrange’s mean value theorem, therefore, there exists some c ∈ ]2, 4[ such that
⇒
⇒
Obviously, c = √6 ∈ ]2, 4[.Hence the Lagrange’s mean value theorem is verified.
Example: Verify Lagrange’s Mean Value Theorem for the function f(x) = x (x -1)(x -2) in [0, 1/2]
Since f is a polynomial, f is continuous in [0, 1/2] and derivable in ]0, 1/2[. Thus there exists c ∈ ]0, 1/2[ such that
...(1)
Now f’(x) = (x - 1) (x - 2) + x(x - 1) + x(x - 2)
or f ’(x) = 3x2 - 6x + 2. Now f(0) = 0, f(1/2) = 3/8.
From (1), 3/8 = 1/2(3c2 - 6c + 2)
or 12c2 - 24c + 5 = 0 or c =
Now
Thusand the theorem is verified.
Example: Let f be defined and continuous in [a - h, a + h] and derivable in ]a - h, a + h[. Prove that there is a real number θ between 0 and 1 such that f(a + h) - f(a - h) = h[f’(a + θh) + f’(a - θh)].
Define φ(x) = f(a + hx) - f(a - hx) on [0, 1]. ...(1)
∴ φ’(x) = hf' (a + hx) + hf' (a - hx). ...(2)
As x varies over [0, 1], a + hx varies over [a, a + h] and a - hx varies over [a - h, a]. Thus
- φ is continuous in [0, 1].
- φ is derivable in ]0, 1[.
By Lagrange's mean value theorem, there exists θ, 0 < θ < 1, satisfying
φ’(θ) or φ(1) - φ(0) = φ’(θ).
Hence f(a + h) - f(a - h) = h [f' (a + θh) + f’(a - θh)], by (1) and (2).
Example: Let f be defined and continuous on [a - h, a + h] and derivable on ]a - h, a + h[. Prove that there is real number θ between 0 and 1 for which f(a + h) - 2f(a) + f(a - h) = h[f(a + θh) - f(a - θh)].
Consider φ(x) = f(a + hx) + f(a - hx) on [0, 1].
Then (i) φ is continuous in [0, 1], (ii) φ is derivable in ]0, 1[. So by Lagrange’s mean value theorem.for some θ ∈ ]0, 1[
or φ(1) - φ(0) = φ(θ)
or [f(a + h) + f(a - h)] - [f(a) + f(a)] = h[f'(a + θh) - f'(a - θh)].
Hence f(a + h) - 2f(a) + f(a - h) = h[f'(a + θh) - f'(a - θh)].
Example: Prove that if f be defined for all real x such that | f(x) - f(y) | < (x - y)2 for all real x and y, then f is constant.
Let c ∈ R. For x ∈ c, we have
using (1).
If ε > 0, then on choosing δ = ε, we obtainwhen |x - c| < δ.
∴
Thus f’(x) = 0 ∀ x ∈ R.
Hence f is a constant function.
Example: Use mean value theorem to prove that 1 + x < ex < 1 + xex, ∀ x > 0.
We shall apply Lagrange’s mean value theorem to the function f(x) = ex in the interval [0, x]. The function f(x) = ex is derivable in [0, x] and, therefore, there exists some c, 0 < c < x, such that
...(1)
Since 0 < c < x, so 1 = e° < ec < ex. ...(2)
From (1) and (2), 1 < (1/x) (ex - 1) < ex or x < ex - 1 < xex. (∵ x > 0)
Hence 1 + x < ex < 1 + xex ∀ x > 0.
Example: Show that 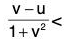 tan-1 v - tan-1 u
tan-1 v - tan-1 u 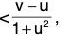 if 0 < u < v, and deduce that
if 0 < u < v, and deduce that 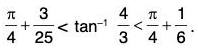
Applying Lagrange’s mean value theorem to the function
f(x ) = tan-1 x in [u, v], we obtainfor some c ∈ ] u, v [
orfor u < c < v. ...(1)
Now c > u ⇒ 1 + c2 > 1 + u2 ⇒...(2)
Again c < v ⇒ 1 + c2 < 1 + v2 ⇒...(3)
From (1), (2), (3) ; we obtain
Hence...(4) (∵ u < v ⇒ v - u > 0)
Taking u = 1 and v = 4/3 in (4), we obtainor
Hence
Example: Prove that |tan-1 x - tan-1 y| ≤ |x - y| ∀ x, y ∈ R.
Let f(t) = tan-1 t in [x, y], where x < y.
By Lagrange’s mean value theorem, there exists some c ∈ ]x, y[ such that f(y) - f(x) = (y -x) f'(x).
or f(y) - f (x) = (y - x). 1/(1+c2)
∴ f(y) - f(x) ≤ (y - x).
Similarly, f(x) - f(y) ≤ (x - y), when y < x.
∴ |f(x) - f(y)| = |x - y|.
Hence, |tan-1 x - tan-1 y|≤|x - y| ∀ x, y ∈ R.
Example: Let f be differentiable on an interval I and suppose that fs is bounded on I. Prove that f is uniformly continuous on I.
Let x1, x2 be any two arbitrary points of I with x1 < x2. Suppose f’(x) is bounded on I, there exists some k > 0 such that
|f'(x)| ≤ k ∀ x ∈ |. ...(1)
Applying Lagrange’s mean value theorem to f on [x1, x2], we getfor some c ∈ ]x1, x2[
or | f(x2) - 1(x1) | = | x2 - x1 | | f’(c) | ≤ k I x2 - x1 I, by (1).
Let ε > 0 be given and let δ = ε/k > 0. Then | f(x2) - f(x1) | < ε, when | x2 - x1 | < δ, ∀ x1, x2 ∈ |.
Hence f is uniformly continuous on I.
Second Mean Value Theorem :
Cauchy’s Mean Value Theorem : Statement:
If two functions f and g with domain [a, b] are such that both are
[C1] continuous in [a, b]
[C2] differentiable in (a, b), and
[C3] g’(x) ≠ 0 ∀ x ∈(a, b) then ∃ c ∈ (a, b) such that: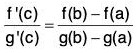
Proof. First we notice that g(b) ≠ g(a)
Let, if g(b) = g(a), then g would satisfy all the conditions of Rolle’s theorem, particularly [R3], then by the theorem, ∃ c ∈(a, b), where g’(c) = 0 which contradicts the condition [C3].
Therefore our assumption g(a) = g(b) is false.
Hence g(a) ≠ g(b) ...(1)
Now define a new function φ, with domain [a, b] involving the given functions f and g as follows: φ(x) = f(x) + A g(x), ...(2)
where A is a constant to be determined such that φ(a) = φ(b)
or, f(a) + A f(b) = g(a) + A g(b) [by (2)]
⇒ 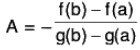 ...(3)
...(3)
which exists because g(b) ≠ g(a).
Hence the function φ is expressed as sum of two continuous and derivable functions, therefore φ is :
- continuous on [a, b]
- differentiable on (a, b) and
- φ(a) = φ(b) [by A of (3)]
Thus the given function φ satisfies all the three conditions of Rolle’s theorem. Therefore Rolle’s theorem is applicable and accordingly there must be atleast one point x = c in (a, b), where φ'(c) = 0.
∴ φ’(c) = f’(c) + A g'(c) = 0
⇒ 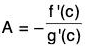 ...(4)
...(4)
By (3) and (4), 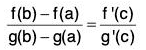 Hence Proved.
Hence Proved.
Important Special Case
When g(x) = x, it reduces to Lagrange’s MV Theorem.
Geometrical interpretation of Cauchy’s Mean value Theorem
Statement : There is an ordinate x = c between x = a and x = b such that the tangents at the points where x = c cut the graph of the function f(x) and 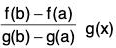 are mutually parallel.
are mutually parallel.
Another useful form of Cauchy’s Mean Value Theorem:
Statement: If two functions f(x) and g(x) with domain [a, a + h] are such that both are:
- Continuous in [a, a + h],
- Differentiable in (a, a + h), and
- g’(x) ≠ 0, x ∈ (a, a + h)
then ∃ θ ∈ (0, 1) such that :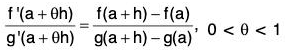
If we put b = a + h, then any point c = a + θh , 0 < θ < 1 may be taken in the interval [a, a + h].
Generalised Mean Value Theorem
If three functions f, g and h defined in [a, b] are such that
- f, g and h are continuous in [a, b]
- f, g and h are derivable in ]a, b[.
Then there exists a real number c ∈ ]a, b[ such that
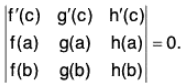
Proof. Define a function ψ on [a, b] as follows :
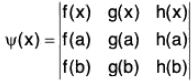
or y(x) = A f(x) + B g(x) + C h(x), ...(iii)
where A = g(a) h(b) - h(a) g(b) etc., B and C are constants.
Applying given conditions (i) and (ii) in (iii), it follows that y is continuous in [a, b] and derivable in ]a, b[.
Also ψ(a) = 0 = ψ(b). (∵ two rows in ψ(x) become identical by putting x = a and x = b)
So ψ(a) = φ(b).
Thus ψ satisfies all the conditions of Rolle’s theorem and, therefore, there exists some c ∈ ]a, b[ such that ψ’(c) = 0.
Now 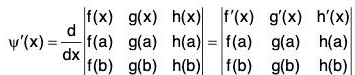
Hence 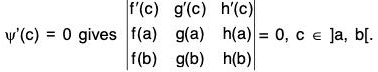
Remarks 1. If we take g(x) = x and h(x) = 1 in the Generalised Mean Value Theorem, we obtain Lagrange’s mean value theorem.
2. If we take h(x) = 1 in the Generalised Mean Value Theorem we obtain Cauchy’s mean value theorem.
Example : Verify the Cauchy’s mean value theorem for :
(i) f(x) = x2, g(x) = x3 in [1, 2].
(ii) f(x) = sin x, g(x) = cos x in [-π/2, 0]
(iii) f(x) = ex, g(x) = e-x in [0, 1].
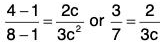
(i) Clearly f(x) = x2, g(x) = x3 are continuous in [1, 2] and derivable in ]1 , 2[. Further g’(x) = 3x2 ≠ 0 ∀ x ∈]1, 2[. Thus the conditions of the Cuachy’s mean value theorem are satisfied and so there exists some point c ∈]1, 2[ such that
or
or
Hence Cauchy’s mean value theorem is verified.(ii) Clearly f(x) = sin x, g(x) = cos x are continuous in [-π/2, 0] and derivable in ] -π/2, 0[. Further g’(x) = - sin x ≠ 0 for all x ∈ ] -π/2, 0 [. Thus the conditions of the Cauchy’s mean value theorem are satisfied and so there exists some point c ∈ ] - π/2, 0 [ such that
or tan c = -1, which gives c = - π/4 ∈ ] - π/2, 0[.
Hence Cauchy's mean value theorem is verified.(iii) Clearly f(x) = ex and g(x) = e-x satisfy the conditions of the Cauchy’s mean value theorem and so there exists some c ∈ ]0, 1[ such that
or
or 2c = 1 or c = 1/2 ∈]0, 1[.
Hence Cauchy's mean value theorem is verified.
Example : Show that 
Let f(x) = sin x, g(x) = cos x ∀ x ∈ [α, β] and derivable in ]α, β[.
Further g’(x) = - sin x ≠ 0 ∀ x ∈ ]a, b[ ∈ ]0, π/2[.
By Cauchy’s mean value theorem,
i e.,
Hence
Example : Let the function f be continuous in [a, b] and derivable in ]a, b[. Show that there exists a number c in ]a, b[ such that 2c [f(a) - f(b)] = f’(c) [a2 - b2].
Let g(x) = x2 ∀ x ∈ [a, b], a < b.
Then f and g are continuous in [a, b] and derivable in ]a, b[. Further g’(x) = 2x ∉ ]a, b[. By Cauchy’s mean value theorem,
i.e.,
Hence 2c [f(a) - f(b)] = f(c) [a2 - b2], c ∈ ]a, b[
Example : If f and g’ exist for all x ∈ [a, b] and if g’(x) ≠ 0 ∀ x ∈ ]a, b[, then prove that for some c ∈ ]a, b[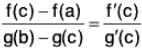
Define a function ψ on [a, b] as follows :
ψ(x) = f(x) g(x) - f(a) g(x) - g(b) f(x), ∀ x ∈ ]a, b[.
Since f and g are derivable in [a, b], so ψ is continuous in [a, b] and derivable in ]a, b[.
Also ψ(a) = ψ(b) = -f(a) g(b).
Since ψ satisfied all the conditions of Rolle’s Theorem, therefore, there exists some c ∈ ]a, b[ such that ψ’(c) = 0. We have
ψ’(x) = f'(x) g(x) + f(x) g’(x) - f(a) g’(x) - g(b) f'(x).
∴ ψ'(c) = 0 gives us
f’(c) g(c) + f(c) g’(c) - f(a) g’(c) - g(b) f(c) = 0
or g’(c) (f(c) - f(a} = f’(c) (g(b) - g(c)}.
Hence
Example : If a function f is such that its derivative f’ is continuous on [a, b] and derivable on ]a, b[, then show that there exists a number c between a and b such that f(b) = f(a) + (b - a) f'(a) + 1/2(b - a)2f"(c).
Define a function φ on [a, b] as follows :
φ(x) = f(b) - f(x) - (b - x) f'(x) - (b - x)2 A, ...(1)
where A is a constant to be determined by
φ(a) = φ(b) ...(2)
i.e., f(b) - f(a) - (b - a) f (a) - (b - a)2 A = 0
i.e., f(b) = f(a) + (b - a) f (a) + (b - a)2 A. ...(3)
Since f is continuous on [a, b], so f is also continuous on [a, b].
Also (b - x), (b - x)2 are continuous on [a, b].
Thus by (1), φ is continuous.
Thus φ satisfies the conditions of Rolle’s Theorem and so there exists some point c ∈ ]a, b[ such that φ’(c) = 0. ...(4)
From (1), φ’(x) = - f'(x) - {-f(x) + (b - x) f"(x)} + 2(b - x)A
or φ’(x) = - (b - x) f”(x) + 2(b - x) A. ...(5)
∴ f ’(c) = 0 ⇒ - (b - c) f'’(c) + 2(b - c) A = 0
⇒ A = 1/2f"(c), since a < c < b ⇒ b - c ≠ 0.
Substituting this value of A in (3), the result is proved.
Example : If f is continuous on [a, a + h] and derivable on ] a, a + h [, then prove that there exists a real number c between a and a + h such that f(a + h) = f(a) + hf’(a) +h2/2 f" (c).
Define a function φ on [a, a + h] as follows:
φ(x) = f(x) + (a + h - x) f'(x) + 1/2(a + h - x)2 A. ...(1)
where A is a constant to be determined by φ(a) = φ(a + h)
i.e., f(a) + hf’(a) + h2/2 A = f(a + h). ...(2)
Since f is continuous on [a, a + h], f and F are continuous on [a, a + h]. Further (a + h - x), (a + h - x)2 are also continuous on [a, a + h] and so by (1), φ is continuous on [a, a + h]. Since f is derivable on ]a, a + h[, so by (1), φ is derivable on ]a, a + h[. Thus φ satisfies all the conditions of Rolle’s Theorem and so there exists some c ∈ ] a, a + h [ such that
∴ f’(c) = 0 ...(3)
From (1), φ’(x) = f'(x) - f'(x) + (a + h - x) f"(x) - (a + h - x) A.
∴ 0 = φ’(c) = (a + h - c) [f’(c) - A] ...(4)
⇒ f"(c) - A = 0, since c ∈ ]a, a + h[ means a + h - c ≠ 0.
Putting A = f”(c) in (2), we obtain
f(a + h) = f(a) + h f'(a) + 1/2 h2f"(c).
Example : Let f and g be two functions defined and continuous on [a, b] and derivable on (a, b). Show that there exists some c ∈ (a, b) such that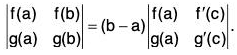
We define a function φ on [a, b] as follows :
...(1)
By the given hypothesis, φ is continuous on [a, b] and derivable on (a, b). Also φ(a) = 0 = φ(b). Thus φ satisfies the conditions of Rolle’s theorem and so there exists some point c ∈ (a, b) such that φ’(c) = 0.
From (1), we have
∴
Hence
Example : If f” be continuous on [a, b] and derivable on ]a, b[, then prove that
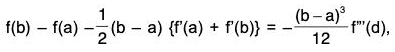 for some real number d between a and b
for some real number d between a and b
Define a function g on [a, b] as follows ;
g (x ) = f(x) - f(a) - (1/2)(x - a) {f'(a) + f'(x)} + A (x - a)3,where A is a constant to be suitably chosen.
Since f” is continuous on [a, b], so f and f are continuous on [a, b].
Thus g is continuous on [a, b].
Similarly, g is derivable on ]a, b[.
Let A be chosen such that g(a) = g(b).
∴ 0 = f(b) - f(a) - 1/2(b-a) {f'(a) + f(b)} + A (b - a)3. ...(1)
Since the function g satisfies all the conditions of Rolle’s theorem [a, b], therefore, there exists a real number c between a and b such that
g’(c) = 0
We have g'(x) = f'(x) - (1/2){f'(a) + f'(x)} - 1/2(x-a)f"(x) + 3A (x-a)2
or g'x = 1/2{f'(x) - f'(a)} - 1/2 (x - a)f"(c) + 3A(c - a)2 = 0.
Thus g’(c) = 0 implies that
1/2{f'(c) - f'(a)} - 1/2(c-a)f"(c) + 3A(c-a)2 = 0. ...(2)
Let h be a function defined on [a, b] as follows :...(3)
Then (i) h is continuous on [a, c],
(ii) h is derivable on ]a, c[,
(iii) h(c) = 0 and h(a) = 0, by (2) and (3); so that h(a) = h(c).
Since the function h satisfies all the conditions of Rolle’s theorem it [a, c], therefore, there exists a real number d(a < d < c < b), such that
h'(d) = 0.
From (3),
∴ 0 = h'(d) = -(1/2)(d-a)f"(d) + 6A (d-a).
i.e., A = f”’(d)/12, since (d - a) ≠ 0. ...(4)
From (1) and (4), we have
Example : Assuming that f”(x) exists for all x in [a, b], show that 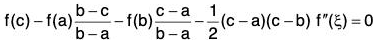 ...(1)
...(1)
where c and ξ both lie in [a, b].
The equation (1) can be rewritten as
f(c)(b-a) -f(a)(b-c) -f(b)(c-a) - 1/2(b-a)(c-a)(c-b)f"ξ = 0
or f(a)(c-b) -f(c-a) -f(c)(b-a) - 1/2(a-b)(b-c)(c-a)f"ξ = 0
or...(2)
We shall prove (2) instead of (1).
The relation (2) helps us to define a function F(x) on [a, b] as follows:...(3)
where A is a constant such that F(c) = 0. ...(4)
From (3), F(a) = 0, F(b) = 0.
Thus F(a) = F(c) and F(c) = F(b), a < c < b. ...(5)
Since f” exists in [a, b], therefore, f and f are derivable and continuous in [a, b]l an hence derivable on continuous in each of the intervals [a, c] and [c, b]. From (3) and (5), it follows that F satisfies the conditions of Rolle’s theorem in each of the intervals [a, c] and [c, b]. Consequently,
and
From (3),...(6)
As stated earlier, f is derivable and continuous in [a, b]. So by (6), F’ is derivable and continuous in [ξ1, ξ2] ⊂ [a, b] and F’(ξ1) = F’(ξ2). Thus F’ satisfies the conditions of Rolle’s theorem in [ξ1, ξ2] and so there exists x ∈ ]x1, x2[ c: [a, b] such that
F"ξ = 0
From (6), F”(x) =
= f”(x)(b - a) - 2A (b - a)
∴ F"(ξ) = 0 ⇒ f"(ξ)-2A = 0 ⇒ A = -(1/2)f"(ξ). (∵ a≠b)
Substituting A = 1/2f"(ξ) in F(c) = 0 and using (3), we obtain
which proves (2).
Example : If f(0) = 0 and f”(x) exists on [0, ∞[, show that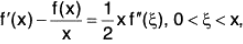 ...(1)
...(1)
and deduce that if f (x) is positive for positive values of x, then f(x)/x strictly increases in ]0, ∞[.
The relation (1) can be written as
f(x) - xf'(x) + (1/2)x2f"(ξ) = 0.
Define a function F as follows :
F(x) = f(x) - x f'(x) + (1/2)Ax2, ...(2)
where A is a constant such that F(c) = 0, where c > 0.
We have F(0) = f(0) = 0 and F(c) = 0. ∴ F(0) = F(c).
Thus F satisfies the conditions of Rolle’s theorem on [0, c].
Therefore, there exists ξ, such that 0 < ξ < c and F’(ξ) = 0.
From (2) F’(x) = - x f"(x) + Ax.
∴ F’(x ) = 0 ⇒ A = f"(ξ).
From (2), F(c) = 0 ⇒ f(c) - cf’(c) + (1/2)Ac2 = 0
⇒
Hence
(ii) Let G(x) = f(x)/x, whenever x > 0.
∴
Thus G’(x) > 0 ∀ x > 0. ...(3)
If x1 and x2 be any two positive real numbers such that x2 > x1, then by applying Lagrange’s mean value theorem to G in [x1, x2], we get
G(x2) - G(x1) = (x2 - x1) G’(θ), θ ∈ ]x1, x2[
Since G’ (θ) > 0, by (3), and x2 - x, > 0, so
G(x2) - G(x1) > 0 i.e ., G(x2) > G (x1) for x2 > x1 > 0.
Hence G(x) = f(x)/x is strictly increasing in ]0, ∞[.
Example : A twice differentiable function f is such that f(a) = f(b) = 0 and f(c) > 0 for a < c < b. Prove that there is at least one value ξ between a and b for which f"(ξ) < 0.
Since f” exists in [a, b), therefore f and f both exist and are continuous in [a, b] and as well as in [a, c] and [c, b], since a < c < b. Applying Lagrange’s mean value theorem to f on [a, c] and [a, b], we get
andrespectively.
Since f(a) = f(b) = 0, the above relationship become...(1)
Since f ’ is continuous and derivable on [ξ1, ξ2] so on applying Lagrange’s mean value theorem off’ on [ξ1, ξ2], we obtain...(2)
From (1) and (2), we get
since f(c) > 0, a < c < b and ξ1 < ξ2.
Hence f"( ξ) < 0 for some a < ξ < b.
Example : If f ” be defined on [a, b] and if |f ’(x)| ≤ M for all in [a, b], then prove that |f(b) - f(a) - 1/2 (b - a) (f(a) + f(b)}| ≤ (1/2)(b-a)2M.
Define a function φ on [a, b] as follows :
φ(x) = f(x) - f(a) - (1/2)x-a {f'(a) + f'(x)} + A(x-a)2, ...(1)
where A is a constant to be chosen such that φ(b) = 0 ...(2)
i.e., f(b) - f(a) -(1/2)(b-a){f'(a) + f'(b)} + A(b-a)2 = 0. ...(3)
Since f” is defined on [a, b], so f and f are both derivable on [a, b] i.e., φ is derivable on [a, b] and so φ is continuous on [a, b].
From (1) and (2), φ(a) = 0, φ(b) = 0 and so φ(a) = φ(b)
By Rolle’s Theorem, there exists some c ∈ ]a, b[ such that
φ'c = 0
From (1)
∴ φ’(c) = 0 ⇒ f’(c) - f'(a) - (c - a) f"(c) + 4 A(c - a) = 0. ...(4)
Applying Lagrange’s Mean Value Theorem to f on [a, c], we obtain
f(c) - f(a) = (c - a) f"(d) for some d ∈ ]a, c[.
Substituting in (4), we obtain
f”(d) - f"(c) + 4 A = 0 ⇒ A = 1/4[f"(c) - f"(d)]/
Putting this value of A in (3), we obtain
f(b) - f(a) - 1/2(b-a){f'(a) + f'(b)} = 1/4(b-a)2[f"(d)-f"(c)].
Hence | f(b) - f(a) - (1/2)(b-a){f'(a)+f'(b)}|
≤ (1/4)(b-a)2[|f"(d)| + |f"(c)|]
≤ (1/4)(b-a)2 (M+M) {∵ | f"(x)| ≤ M ∀ x ∈ [a, b]}
= (1/4) b-a)2M.
Example : Show that ‘0’ which occurs in the Lagrange's mean value theorem tends to the limit 1/2 as h → 0, provided f” is continuous.
We may take f” to be continuous in [a, a + h].
So by Example we have
f(a + h) = f(a) + hf’(a) + (h2/2)f"(a + θ1h), where 0 < θ1 < 1. ...(1)
Applying Lagrange’ mean value theorem to f in [a, a + h], we get
f(a + h) - f(a) = hf'(a + θh), 0 < θ < 1. ...(2)
From (1) and (2), we obtain...(3)
Applying Lagrange’s mean value theorem to the function f in [a, a + θh], we obtain
f’(a + θh) - f'(a) = θh. f ’’(a + θ2θh), 0 < θ2 < 1. ...(4)
From (3) and (4), we get
⇒
∴since f" continuous in [a, a + h].
Hence θ → 1/2 as h → 0.
Example : If f”(x) exists ∀ x ∈ [a, b] and 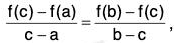 where c ∈ ]a, b[. ...(1)
where c ∈ ]a, b[. ...(1)
Then there exists some ξ ∈ ]a, b[ such that f’’(ξ) = 0.
Since f ’(x) exists ∀ x [a, b], therefore, f and f exist in [a, b] and are continuous in [a, b].
Applying Lagrange’s Mean Value Theorem to the function f on each of the interval [a, c] and [c, d], we getfor some ξ1 ∈ ]a, b[,
andfor some ξ2 ∈ ]c, b[,
Using (1), it follows that f’(ξ1) = f’(ξ2). Further.
(i) f' is continuous in [ξ1, ξ2],(ii) f’ derivable in ]ξ1, ξ2[and (iii) f'(ξ1) = f’(ξ2). So by Rolle’s Theorem as applied to f’ in [ξ1, ξ2], we obtain
f"(ξ) = 0 for some ξ ∈ ]ξ1, ξ2[ ⊂ ]a, b [.
Example : If f”(x) > 0 for all x ∈ R, then show that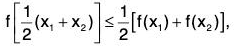 ...(1)
...(1)
for every pair of real numbers x1 and x2.
Let x1, x2 ∈ R be arbitrary. If x1 = x2, then the given relation (1) because equality and so the result follows. We may suppose that x1 < x2. Since f"(x) exists ∀ x ∈ R, if satisfies the conditions of Lagrange's mean value theorem in each of the intervals
Consequently,
and
On subtracting the corresponding sides of these equations, we get...(2)
Since f”(x) exists ∀ x ∈ R, f satisfies the conditions of Lagrange’s mean value theorem in the interval [c1, c2] and so f’(c2) - f'(c1) = (c2 - c1) f”(t), for some t ∈ ]c1, c2[.
As given f”(t) > 0 and c2 > c1, so (c2 - c1) f"(t) > 0.
Thus f'(c2) - f'(c1) > 0 i.e., f’(c1) - f'(c2) < 0.
Also x2 > x1 ⇒ x2 - x1 > 0.
Using these inequalities in (2), we get
Hence
Example : If f', g ’ are continuous on [a - h, a + h] and derivable on ] a - h, a + h [, then prove that 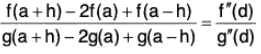 for some d ∈ ] a - h, a + h [, provided g (a + h) - 2g (a) + g (a - h) ≠ 0 and g”(t) ≠ 0 for each t ∈ ] a - h, a + h [.
for some d ∈ ] a - h, a + h [, provided g (a + h) - 2g (a) + g (a - h) ≠ 0 and g”(t) ≠ 0 for each t ∈ ] a - h, a + h [.
We define a function φ on [a - h, a + h] as follows :
φ(x) = f(x) + Ag(x) + Bx + C, ...(1)
where A, B, C are constants to be determined by
φ(a - h) = φ(a) = φ(a + h) = 0. ...(2)
Since f and g are continuous on [a - h, a + h] and Bx + C is also continuous on [a - h, a + h], so by (1), φ is continuous on [a - h, a + h]. Similarly, φ is derivable on ]a - h, a + h[. By virtue of (2), φ satisfies all the conditions of Rolle’s theorem in each of the intervals [a - h, a] and [a, a + h]. Consequently.
φ’(t1) = 0, for some t1 ∈ ]a - h, a[,
and φ’(t2) = 0, for some t2 ∈ ]a, a + h[.
For any x ∈ ]a - h, a + h [, we have by (1),
φ’(x) = f(x) + Ag’(x) + B. ...(3)
Since f' and g’ are continuous on [a - h, a + h], so by (3), φ’ is continuous on [a - h, a + h]. Similarly, 'φ' is derivable on ] a - h, a + h [. Also φ'(t1) = φ'(t2) = 0. Applying Rolle’s theorem to φ’ on [ t1, t2], there exists some d ∈ ]t1, t2[ such that φ”(d) = 0 for some d ∈ ] t1, t2 [. Using (3),
f'’(d) + Ag”(d) = 0 ⇒ A = -f'(d)/g” (d). ...(4)
From (2), φ(a+h) -2φ(a) + φ(a-h) = 0
or [f(a + h) - 2 f(a) + f(a - h)] + A[g(a + h) - 2g(a) + g(a - h)] + [B(a + h) + C - 2 (Ba + C) + B(a - h) + C] = 0
or...(5)
From (4) and (5), we get the desired result.
Example : Show that
(a) (x/1+x) < log (1 + x) < x, x > 0.
(b) (x - (x2/2)) < log (1 + x) < x - (x2/(2(1+x)), x > 0.
(c) (x2/2(1+x)) < x - log (1 + x ) < (x2/2), x > 0.
Let f(x) = log (1 + x)-(x/(1+x), so that f(0) = 0.
We shall show that f(x) > 0 for x > 0.
Now,
Thus f(x) is an increasing function ∀ x > 0
⇒ f(x) > f(0), for x > 0
⇒ f(x) > 0, for x > 0 (∵ f(0) = 0)
⇒ log(1 + x) - (x/1+x) >, 0, x > 0
∴ (x/1+x)< log (1 + x), x > 0.
Let φ(x) = x - log (1 + x), so that φ(0) = 0.
∴for x > 0.
Thus φ(x) is an increasing function of x, for x > 0
⇒ φ(x) > f(0), for x > 0
⇒ φ(x) > 0 (∵ φ(0) = 0)
⇒ x - log (1 + x) > 0, for x > 0
⇒ log (1 + x) < x, for x > 0.
Hence (x/1+x) < log (1 + x) < x, x > 0
(b) Let f(x) = log (1 + x) - (x - (x2/2)), f (0) = 0.
∴(∵ x > 0)
⇒ f(x) is an increasing function of x, for x > 0 ...(2)
⇒ f(x) > f(0), for x > 0 ⇒ f(x) > 0 (∵ f(0) = 0)
⇒ log (1 + x) -for x > 0
∴ (x - (x2/2)) < log (1 + x), x > 0.
Let- log(1 + x), so that φ(0) = 0.
∴(∵ x > 0)
⇒ φ(x) is an increasing function, for x > 0
⇒ φ(x) > φ(0), for x > 0
⇒ f(x) > 0 (∵ f(0) = 0)
⇒- log (1 + x) > 0, for x > 0
∴ log(1 + x) < x- (x2/(2(1+x))), for x > 0
Hence x - (x2/2) < log (1 + x) < - x2(2(1+x), for x > 0
(c) By part (b), we have
or
Hence
Example : Prove that x < sin-1 x < 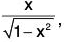 if 0 < x < 1.
if 0 < x < 1.
Let f(x) = sin-1 x - x, so that f(0) = 0.
∴
⇒ f’(x) > 0, for 0 < x < 1
⇒ f is strictly increasing in 0 < x < 1
⇒ f(x) > f(0), for 0 < x < 1 (∵ x > 0)
⇒ f(x) > 0, for 0 < x < 1.
⇒ sin-1 x - x > 0, for 0 < x < 1
⇒ sin-1 x > x, for 0 < x < 1
⇒ x < sin-1 x , for 0 < x < 1.
Let g(x) =- sin-1 x, so that g(0) = 0.
∴
⇒ g’(x) > 0, for 0 < x < 1
⇒ g is strictly increasing, for 0 < x < 1
⇒ g(x) > g(0), for 0 < x < 1 (∵ x > 0)
⇒sin-1 x, for 0 < x < 1
⇒ sin-1 x <, for 0 < x < 1.
Example : Using Lagrange's mean value theorem, show that x/(1+x) < log (1 + x) < x, x > 0.
Let f(x) = log (1 + x) in [0, x ], so that f'(x) = 1/(1+x).
Since f is continuous in [0, x] and derivable in ]0, x[, so by Lagrange’s mean value theorem, there exists some 0, 0 < 0 < 1 such that(∵ ]0, x [ = ]0 x , 1 x [, c = θx)
or log (1 + x) = x/(1+θx). [∵ f(0) = 0] ...(1)
Now 0 < c < 1 and x > 0 ⇒ θx < x
⇒ 1 + 1 + θx < 1 + x ⇒
⇒...(2)
Again 0 < θ < 1 and x > 0 ⇒ y < 1 + θx
⇒...(3)
From (2) and (3), we obtain...(4)
From (1) and (4), we obtain
x/(1+x) < log (1 + x) < x.
Example : Use the mean value theorem to prove 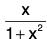 < tan-1 x < x, if x > 0.
< tan-1 x < x, if x > 0.
Let f(x) = tan-1 x in [0, x]
Then f satisfies the conditions of Lagrange’s mean value theorem in [0, x]. Consequently, there exists some θ satisfying 0 < θ < 1 such that
or tan-1 x =...(1)
Now 0 < θ < 1 and x > 0 ⇒ θ2 x2 < x2 ⇒ 1 + θ2 x2 < 1 + x2
⇒...(2)
Again 0 < θ < 1 and x > 0 ⇒ 1 < 1 + θ2 x2
⇒...(3)
From (2) and (3), we obtain...(4)
From (1) and (4), we obtain
x/(1+x2) < tan-1x < x , x > 0.
Example : Show that 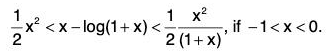
Let f(x ) = x - log (1 + x ) - (1/2)x2, so that f(0) =0.
∴...(1)
Now -1 < x < 0 ⇒ x + 1 > 0 . Thus, by (1),
f'(x) < 0, for -1 < x < 0
⇒ f is decreasing for - 1 < x < 0
⇒ f(x) > f(0), for -1 < x < 0
⇒ f(x) > 0 , for - 1 < x < 0
⇒ 1/2(x2) < x- log (1 + x), for - 1 < x < 0.
Letso that g(0) = 0.
∴
⇒ g’(x) < 0, for -1 < x < 0
⇒ g is decreasing, for -1 < x < 0
⇒ g(x) > g(0), for -1 < x < 0
⇒ g(x) > 0, for -1 < x < 0
⇒ x - log(1 + x)-1 < x < 0
Example : Prove that 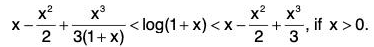
Let f(x) = log(1 + x) -
∴
⇒ f’(x) > 0, for x > 0
⇒ f is increasing, for x > 0
⇒ f(x) > f(0), for x > 0
⇒ f(x) > 0 (∵ f(0) = 0)
⇒
Let
∴ g’(x) = 1 - x + x2 -
⇒ g’(x) > 0, for x > 0
⇒ g is increasing, for x > 0
⇒ g(x) > g(0), for x > 0
⇒ g (x) > 0 (∵ g(0) = 0)
⇒ log (1 + x) < x -
Example: If 0 < x < 1, show that 2x < log 
Let f(x) =
∴
Clearly, f(x) > 0, for 0 < x < 1 ⇒ f is increasing, for 0 < x < 1.
In particular, f(x) > f(0) = 0 as x > 0
∴for 0 < x < 1.
Hencefor 0 < x < 1.
Let g(x) = 2x
∴
Thus g(x) is increasing, for 0 < x < 1. In particular, g(x) > g(0) = 0 ⇒ g(x) > 0
Hence
Example : Prove that tan x > x, whenever 0 < x < π/2.
Let c be any real number such that 0 < c < π/2.
Let f(x) = tan x - x for all x ∈ [0, c].
Then f is continuous as well as derivable on [0, c].
Now f’(x) = sec2 x - 1 = tan2 x > 0, for 0 < x < c.
Thus f is strictly increasing in [0, c]
⇒ f(c) > f(0), for c > 0.
But f(0) = 0. Therefore f(c) > 0 ⇒ tan c - c > 0.
Since c is any real number such that 0 < c < π/2, therefore, tan x > x, whenever 0 < x < π/2.
Example : Show that 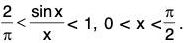
Let f be defined as
...(1)
Then f is continuous in [0, π/2] and derivable in ]0, π/2[.
We have...(2)
Let g(x) = x cos x - sin x in [0, π/2]
∴ g’(x) = cos x - x sin x - cos x
= - x sin x < 0 in ]0, π/2[.
⇒ g is strictly decreasing in [0, π/2).
⇒ (x) < g(0) = 0 in [0, π/2] (∵ x > 0)
Using in (2), it follows that f’(x) < 0 in ]0, π/2[
⇒ is strictly decreasing in [0, π/2]
⇒ f(0) > f(x) > f(π/2), for 0 < x < π/2
⇒using (1)
Hence
Example: Prove that 
Since x sin x > 0 for all x in ]0, π/2[, therefore, we need to show that tan x sin x - x2 > 0, ∀ x ∈]0, π/2[.
Let c any real number in ]0, π/2[.
Let f(x) = tan x sin x - x2 ∀ x ∈ [0, c]
Then f is continuous as well as derivable in [0, c].
Now f’(x) = sec2 x sin x + tan x cos x - 2x
= sin x (sec2 x + 1) - 2x.
The form of f’(x) is such that we cannot decide about its sign.
Let g’(x) = cos x (sec2x + 1) + sin x . 2 sec2x tan x - 2+ 2 sin2 x sec3 x.
Since g’(x) > 0 for all x ∈ ]0, c[⇒ g is strictly increasing in [0, c]
⇒ g(x) > g(0), whenever 0 < x < c. Since g(0) = 0, this means that g(x) > 0, whenever 0 < x < c ⇒ f’(x) > 0, whenever 0 < x < c ⇒ f is strictly increasing in [0, c] ⇒ f(c) > f(0) = 0 ⇒ f(c) > 0.
⇒ tan c sin c - c2> 0
⇒
Since c is any point of ]0, π/2[, it follows thatwhenever 0 < x < π/2.
Example: Verify Lagranges MV Theorem for the function f(x) = |x| in the interval [-1 , 2].
L1. The given function is continuous in [-1, 2], because
and
L2. At the point x = 0 of the open interval (-1, 2)
Thus f’(0 + 0) ≠ f'(0 - 0)
Therefore the given function is not derivable in (-1, 2).
Hence Lagrange's theorem is not applicable for the given function.
Taylor's Theorem
Taylor’s theorem with Lagrange’s form of remainder;
Statement : If a function f with domain [a, a + h] is such that:
(i) fn-1 is continuous in [a, a + h]
(ii) fn exists in (a, a + h)
then ∃ θ ∈ (0, 1) such that :
f(a + h) = f(a) + hf'(a) + 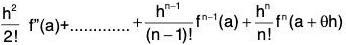
Proof : Let us define a new function φ with domain [a, a + h] involving the derivatives of f as follows:
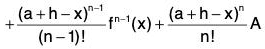 ...(1)
...(1)
where A is a constant to be determined such that
φ (a + h) = φ (a) ...(2)
From (1), φ (a + h) = f (a + h) ...(3)
and 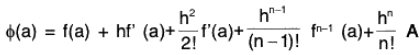 ...(4)
...(4)
Using (3) and (4) in (2), we obtain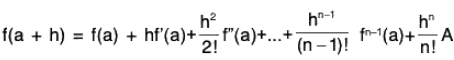 ...(5)
...(5)
The value of A is given by (5).
Now by first condition, f(x), f’(x), f"(x)...fn-1(x) are continuous in [a, a + h] and their derivatives exist and are finite in (a, a + h).
Polynomials of x, (a + h - x), 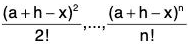 are continuous and derivable for all values of x.
are continuous and derivable for all values of x.
Therefore the function is also continuous in [a, a + h] and derivable in (a, a + h).
Thus the function φ is :
R1. Continuous in [a, a + h]
R2. Derivable in (a, a + h) and
R3. φ(a) = φ(a + h) [by (2)]
Therefore the function φ satisfies all the three conditions of Rolle’s theorem and accordingly, there exists at least one positive number θ, 0 < θ < 1,
where
φ’(a + θh) = 0, 0 < θ < 1 ...(6)
Differentiating (1),
φ‘(x) = f'(x) + [(a + h - x) f"(x) - f'(x)]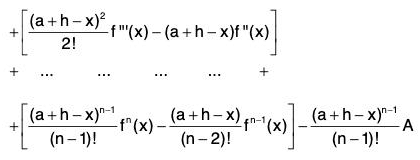
The terms cancel in pairs on RHS, therefore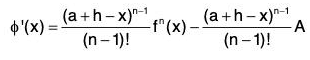
Therefore, 
or, 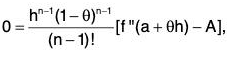 [by (6)]
[by (6)]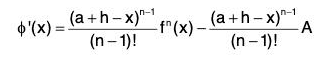
therefore 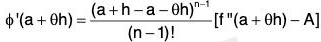
or 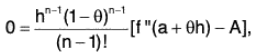 [by(6)]
[by(6)]
⇒ A = f’(a + θh) [∵ h ≠ 0, (1 - θ) ≠ 0] ...(7)
Substituting the value of A from (7) in (5), we obtain the required result.
Hence Proved.
Remainder after n terms [Rn] :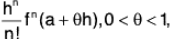
This is also known as Lagrange’s form of Remainder.
Taylor’s theorem with Cauchy’s form of remainder :
Statement: If a function f with domain [a, a + h] is such that
(i) fn-1 is continuous in [a, a + h]
(ii) fn exist in (a, a + h)
then ∃ θ ∈ (0, 1) such that :
f (a + h) = f(a) + h f'(a) + 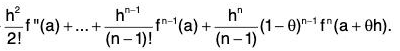
Proof. Consider a function φ defined as follows :
φ(x) = f(x) + (a + h - x) f'(x) + 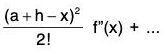
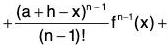 (a + h - x) A ...(1)
(a + h - x) A ...(1)
where A is a constant to be determined such that
φ(a + h) = φ(a) ...(2)
From (1), φ(a + h) = f(a + h) ...(3)
and 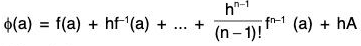 ...(4)
...(4)
Using (3) and (4) in (2),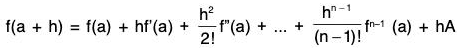 ...(5)
...(5)
The value of A is given by (5).
Now by the first condition.
f(x), f’(x), f’'(x), .... fn-1 (x) are continuous in [a, a + h] and their derivable f'(x), f'’(x), fn(x) exist and are finite in (a, a + h).
and the polynomials (a + h - x), 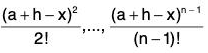 are continuous and derivable for all values of x. Therefore these are continuous in [a, a + h] and derivable in (a, a + h).
are continuous and derivable for all values of x. Therefore these are continuous in [a, a + h] and derivable in (a, a + h).
Thus the function φ is : R1. continuous in [a, a + h]
R2, derivable in (a, a + h)
and R3, φ(a) = φ(b)
Thus the function φ satisfies all the three conditions of Rolle’s theorem, accordingly there exists atleast one positive number θ, 0 < θ < 1, where
φ'(a + θh) = 0, 0 < θ < 1 ...(6)
Differentiating (1), we get
φ’(x) = f'(x) + [(a + h - x) f"(x) - f(x)]
The terms cancel in pairs on RHS, therefore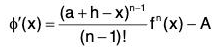
Therefore φ’(a + θh) 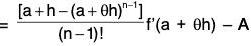
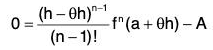 [by (6)]
[by (6)]
⇒  ...(7)
...(7)
Substituting the value of A from (7) in (5), we obtain the required result
Another form :
Replacing h = b - a in the theorem, we get the following use fulform :
f(b) = f(a) + (b - a) f'(a) + 
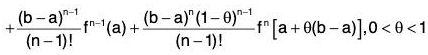
f(a+h) = f(a) + (h)f'(a) + 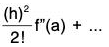
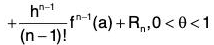
Remainder after n terms [Rn] :

This is known as Cauchy's form of Remainder.
Taylor’s theorem with Schlomitch and Roche form of Remainder.
Statement : If a function f defined in [a, a + h] is such that :
(i) its all derivative up to order (n - 1) i.e. fn - 1 are continuous in [a, a + h]
(ii) fn exists in (a, a + h)
(iii) p ∈ N
then ∃ θ ∈ (0, 1) such that :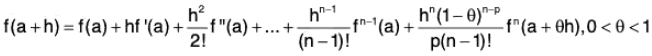
Proof. Consider a function φ defined as follows :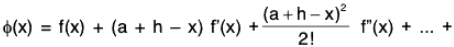
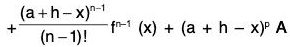 ...(1)
...(1)
where A is a constant to be determined such that
φ(a + h) = φ(a) ...(2)
From (1), φ(a + h) = f(a + h) ...(3)
and 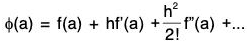
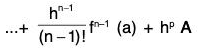 ...(4)
...(4)
Using (3) and (4) in (2), we get
f(a + h) = f(a) + hf’(a) + 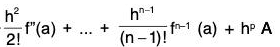 ...(5)
...(5)
The value of A is given by (5).
Now the function φ is :
(R1) continuous in [a, a + h], because f, f', f", .... fn-1, (a - h - x)p are continuous.
(R2) derivable in (a, a + h), because f, f', f" ......fn-1, (a - h - x)p are derivable.
(R3) φ(a + h) = φ(a)
“Thus the function f satisfies all the three conditions of Rolle’s theorem, according ∃θ ∈ (0, 1), where
φ(a + θh) = 0 ...(6)
But 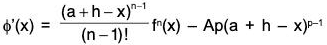
⇒ 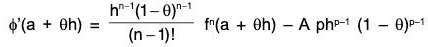
⇒ φ’(a + θh) = 0
⇒ 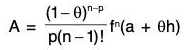 ...(7)
...(7)
Substituting the value of A from (7) in (5), we obtain the required result
Important Special Case :
- When p = n, then Rn(x) = (hn/n!) fn(a+θh),
which is called Lagrange’s form of remainder and we get
Taylor’s theorem with Lagrange’s form of remainder. - When p = 1, then Rn(x) =

which is called Cauchy’s form of remainder and we get Taylor’s theorem with Cauchy’s form of remainder.
Another form :
Replacing a + h = x or h = x - a, we get the following form of Taylor’s theorem :
f(x) = f(a) + (x - a) f(a) + 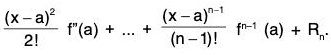
where 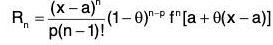 ...(8)
...(8)
is called the remainder after n terms.
Maclaurin’s theorem : Statement :
If a function f with domain [0, x] be such that
- all of its derivatives upto order (n - 1 ) are continuous in [0, x]
- fn exists in (0, x)
 Then ∃ θ ∈ (0, 1) such that
Then ∃ θ ∈ (0, 1) such that
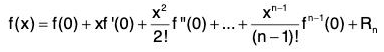
where 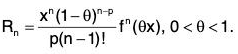
Proof. First of all we observe that condition (i) in the statement of theorem implies that f, f', f", fn-1 are all defined (i.e., exist) and continuous on [0, x].
Consider the function φ defined on [0, x] as
φ(t) = f(t) + (x - t) f'(t) + 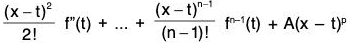
where A is a constant to be determined such that φ(0) = φ(x).
But 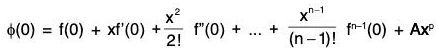
and φ(x) = f(x)
∴ φ(0) = φ(x)
⇒ f(x) = f(0) + xf’(0) 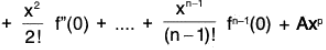 ...(1)
...(1)
Now, (i) Since f, f', f", ... fn-1 are all continuous on [0, x ] and (x - t)r, r ∈ N is continuous on R.
∴ φ is continuous on [0, x].
(ii) Since f, f’, f” ...... fn-1 are all derivable on (0, x) and (x - t)r, r ∈ N is derivable on R.
∴ φ is derivable on (0, x).
(iii) Also φ(0) = φ(x)
Thus the function φ satisfies all the three conditions of Rolle’s Theorem on [0, x] and, hence, there exists a real number φ ∈ (0, 1) such that φ’(θx) = 0.
But φ’(t) = f'(t) - f'(t) + (x - t) f"(t) - (x - t) f"(t) + ... 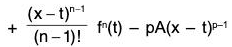
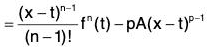 [other terms cancel in pairs]
[other terms cancel in pairs]
⇒ 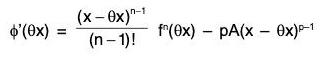
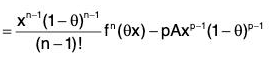
∴ φ’(θx) = 0
⇒ 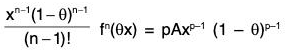
⇒ 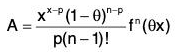
Putting this value of A in (1), we have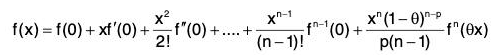
The term 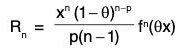 which occurs after n terms in known as Schlomilch and Roche’s form of remainder.
which occurs after n terms in known as Schlomilch and Roche’s form of remainder.
Note. (i) For p = 1, we get Rn = 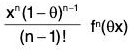 called Cauchy’s form of remainder.
called Cauchy’s form of remainder.
(ii) For p = n, we get Rn = (xn/n!)(fn(θx) called Lagrange’s form of remainder.
Example : Prove that the number ‘θ’ which occurs in the Taylor’s theorem with Lagrange’s form of remainder after n terms approaches the limit 1/(n+1) as h approaches zero provided that fn+1 (x) is continuous and different from zero at x = a.
By Taylor’s theorem with Lagrange' s form of remainder after n terms and (n + 1) terms successively, we have
f(a + h) = f(a) + hf’(a) + ... +where 0 < θ < 1.
f(a + h) = f(a) + hf’(a) + . . . +where 0 < θ1 < 1
On subtraction, we get 0or
...(1)
Using Lagrange’s mean value theorem for fn(x) on [a, a + θh], we have
fn(a + θh) = fn(a) + 0hfn+1 (a + θ2θh) where 0 < θ2 < 1
or fn(a + θh) - fn(a) = θhfn+1 (a + θ2θh) ...(2)
From (1) and (2), we have
∴
= 1/(n+1). [∵ fn+1 (a) ≠ 0]
Ex : Assuming the derivatives which occur are continuous, apply the mean value theorem to prove that φ'(x) = F'{f(x)} f'(x) where φ(x) = F {f(x)}.
Let f(x) = t so that φ(x) = F(t)
Now[∵ f(x + h) = f(x) + hf'(x + θ1h) by Mean Value Theorem]
[∵ F(t + H) = F(t) + HF’(t + θ2H) by Mean Value Theorem]
= f'(x) F'(f(x)) [∵ f and F’ are continuous]
= F’{f(x)} f'(x).
Example : Using Taylor’s theorem, show that
(i) cos x ≥ 1 - (x2/2) ∀ x ∈ R
(ii) 1 + x + (x2/2) < ex < 1 + x + (x2/2)ex, x > 0
(iii) x - (x3/3!) < sin x < x, x > 0
(iv) 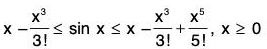
(i) Case 1. Let x = 0
The cos x = 1, 1 - (x2/2) = 1 ∴ cos x = 1 - x2/2.
Case 2. Let x > 0 and f(x) = cos x
Then f'(x) = - sin x, f"(x) = - cos x
Since f(x) = f(0) + xf’(0) + (x2/2!) f”(θx) where 0 < θ < 1.
∴ cos x = 1 - (x2/2) cos θx
But cos θ < 1 θx, x > 0
∴
Case 3. Let x < 0
Put y = -x so that y > 0
By case 2, cos y > 1 - (y2/2) ⇒
Combining all cases, cos x ≥ 1 - x2/2 ∀ x ∈ R.
(ii) Let f(x) = ex, e > 0, then f’(x) = f'’(x) = ex
Since f(x) = f(0) + xf’(0) + (x2/2!) f”(θx) where 0 < θ < 1
∴ ex = 1 + x + x2/2 (eθx)
Now 0 < θ < 1 and x > 0 ⇒ 0 < θx < x
⇒ e0 < eθx < ex [∵ ex is an increasing function]
⇒
⇒ 1 + x + x2/2 < ex < 1 + x + x2/2 (ex).
(iii) Let f(x) = sin x, x > 0, then f’(x) = cos x, f"(x) = - sin x
f”(x) = - cos x
Since f(x) = f(0) + xf’(0) +where 0 < θ < 1
∴ sin x = x - (x3/3!)cos θx
But cos θx < 1 ∀θx, x > 0
∴ x - (x3/3!) cosθ x > x - x3/3!
⇒ sin x > x - x3/3! ...(1)
Also f(x) = f(0) + xf’(θx) where 0 < θ < 1
∴ sin x = x cos θx
But cos θx < 1 ∀ θx, x > 0
∴ x cos θx < x ⇒ sin x < x ...(2)
Combining (1) and (2), we get x - (x3/3!) < sin x < x.
(iv) Case 1. Let x = 0
Then
Case 2. Let x > 0 and f(x) = sin x
Then f'(x) = cos x, f'’(x) = - sin x, f”(x) = - cos x,
fiv(x) = sin x, fv(x) = cos x
Since f(x) = f(0) + x f’(0) +
∴ sin x = x - (x3/3!) cos θx
But cos θx < 1 ∀ θx, x > 0
∴
⇒ sin x > x - (x3/3!) ...(1)
Also f(x) = f(0) + xf’(0) +
∴ Sin x = x -
But cos θx < 1 ∀ θx, x > 0
∴
⇒ sin x < x -...(2)
Combining (1) and (2),
Combining the two cases, we have
Taylor’s Series :
If a function f is defined in the interval [a + ah] and satisfy all conditions of Taylor’s theorem, then by Taylor’s theorem,
f(a + h) = f(a) + hf '(a) +
or, f(a + h) = Sr + Rn, where Sn represents the sum of first n terms and Rn is called the Taylor’s remainder after n terms.
or, f(a + h) = 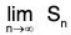
Therefore if the function f is expressible in an Infinite series, then clearly
- fn (a) exists ∀ n ∈ N and
- for the convergence of the Taylor’s series,
Taylor’s remainder after n terms, Rn → 0 when n → ∞, then
f(a + h) = f(a) + h f'(a) +
The infinite series on RHS is known as Taylor’s Series.
Maclaurin’s Series :
When a = 0 and replace h by x, the n the Taylor’s series reduces to the following form :
f(x) = f(0) + xf’(0) + 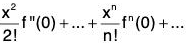
This series is called Maclaurin’s Series and is very useful in the expansion of functions.
Example : Expand ex as an infinite series.
Let f(x) = ex so that fn(x) = ex and fn(0) = e0 = 1 ∀ n ∈ N
Clearly, f and all its derivatives exist and are continuous for every real value of x.
Lagrange’s form of remainder is
Let
so that
⇒
⇒
∴
Thus the conditions of Maclaurin's infinite expansion are satisfied.
∴ For all x ∈ R, ex = f(x)
Example : Expand sin x as an infinite series.
Let f(x) = sin x so that fn(x) = sin
and fn(0) = sin (nπ/2) ∀ n ∈ N
⇒
⇒ f”(0) = fiv(0) = ... = 0, f’(0) = 1, f”(0) = -1, f(0) = 1, ....
Clearly, f and all its derivatives exist and are continuous for every real value of x.
Lagrange’s form of remainder is
∴
But
∴
Thus the conditions of Maclaurin’s infinite expansion are satisfied.
∴ For all x ∈ R, sin x = f(x) = f(0) + xf’(0) +
Example : Expand (1 + x)m, m ∈ R.
Two cases arise according as m is not a positive integer.
Case 1. When m is a positive integer.
Let f(x) = (1 + x)m, x ∈ R
Then fn(x) exists for all x and all n.
In fact, if 1 ≤ n ≤ m, then fn(x) = m(m - 1)(m - 2) ... (m - n + 1) (1 + x)m-n
so that fm(x) = m ! and fn(x) = 0, if n > m
⇒
Since fn(x) = 0 for all n > m, it follows that Rn → 0 as n → ∞. Thus the conditions of Maclaurin’s expansion are satisfied.
∴ (1 + x)m = f(x) = f(0) + xf’(0)
Case 2. When m is not a positive integer.
Let f(x) = (1 + x)m, x ≠ - 1
Taking Cauchy form of remainder, we have
Now let
so that
∴
It follows that if |-x| = |x| < 1, then
⇒...(1)
Since 0 < θ < 1 and -1 < x < 1
∴ -θ < θx < θ ⇒ 1 - θ < 1 + θx < 1 + θ
⇒ 0 < 1 - θ < 1 + θx ⇒
Consequently,...(2)
Also, since -
⇒...(3)
From (1), (2) and (3), we find that for I x I < 1,
Thus the conditions of Maclaurin's infinite expansion are satisfied and
Example : Expand log (1 + x) as an infinite series.
Let f(x) = log (1 + x) where 1 + x > 0 i.e., x > -1
Then
Case 1. When 0 ≤ x ≤ 1
Writing Lagrange’s remainder after n terms, we have
If x = 1, then |Rn| =
∴
If 0 ≤ x < 1, then since 0 < θ < 1
∴ 0 ≤ x < 1 + θx
⇒⇒
∴
∴
Case 2. When -1 < x < 0
Since in this case,need not be less than unity, therefore, it may not be easily shown that Rn → 0 as n → ∞ by considering Lagrange’s remainder.
∴ Writing Cauchy’s remainder after n terms, we have
Now -1 < x < 0 and 0 < θ < 1 ⇒ - θ < θx
⇒ 1 - θ < 1 + θx ⇒
Also, -|x| ≤ x ⇒ - θ |x| ≤ θx
⇒ 1 - |x| < 1 + θx ⇒
Consequently,
and |x|n → 0 as n → ∞ (since |x| < 1)
∴
Thus, we find that if -1 < x ≤ 1, then
Hence log(1 + x) = f(x) = f(0) + x f’(0) +
= log 1 + x.1 +
MAXIMA AND MINIMA OF ONE VARIABLE
Let I be an interval.
A function f : I → R is said to have a global maxima (or an absolute maximum) on I if there exists a point c ∈ I such that f(c) ≥ f(x) for all x ∈ I. c is said to be a point of global maxima for f on I.
f is said to have a global minima (or an absolute minimum) on I if there exists a point c ∈ I such that f(c) ≤ f(x) for all x ∈ I. c is said to be a point of global minima for f on I.
A function f : I → R is said to have a local maximum (or a relative maximum) at a point c ∈ I if there exists a neighbourhood N (c, δ) of c such that f(c) ≥ f(x) for all x ∈ N (c, δ) ∩ I.
f is said to have a local minimum (or a relative minimum) at a point c e I, If there exists a neighbourhood N(c, δ) of c such that f(c) ≤ f(x) for all x ∈ N(c, δ) ∩ I.
We say that f has a local extremum (or a relative extremum) at a point c ∈ I, if f has either a local maximum or a local minimum at c.
Note : If f : I → R has a local maximum (a local minimum) at a point c ∈ I then c is a point of global maxima (a point of global minima) for f on N(c, δ) ∩ I for some suitable δ > 0.
N (c, δ) = (c - δ, c + δ)
Theorem : Let f : I → R be such that f has a local extremum at an interior point c of I. If f’(c) exists then f’(c) = 0.
Proof. We prove that theorem for the case when f has a local maximum at c. The proof of the other case is similar.
Since f’(c) exists, either f'(c) > 0, or f'(c) < 0, or f'(c) = 0.
Let f'(c) > 0. Then 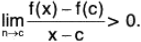
Therefore there exists a positive δ such that 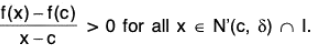
Let c < x < c + δ. Then x - c > 0 and therefore f(x) > f(c) for all x ∈ (c, c + δ). This contradicts that f has a local maximum at c.
Consequently, f’(c) ≥ 0 ....... (i)
Let f ’(c) < 0. Then 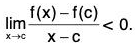
Therefore there exists a positive δ such that 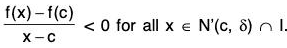
Let c - δ < x < c. Then x - c < 0 and therefore f(x) > f(c) for all x ∈ (c - δ, c). This contradicts that f has a local maximum at c.
Consequently, f’(c) ≤ 0 ....... (ii)
From (i) and (ii) we have f'(c) = 0.
This completes the proof.
Corollary : Let f : I 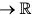 and c be an interior point of I, where f has a local extremum. Then either f’(c) does not exist, or f'(c) = 0.
and c be an interior point of I, where f has a local extremum. Then either f’(c) does not exist, or f'(c) = 0.
Note 1. The theorem says that if the derivative f(c) exists at an interior point c of local extremum, f’(c) must be 0. A function may, however have a local extremum at an interior point c of its domain without being differentiable at c. For example, the function defined by f(x) = |x|, x ∈ R has a local minimum at 0 but f'(0) does not exist.
Note 2. The condition f’(c) = 0 (when f'(c) exists) is only a necessary condition for an interior point c to be a point of local extremum of the function f.
For example, for the function f defined by f(x) = x3, x ∈ R, 0 is an interior point of the domain of f. f’(0) = 0 but 0 is neither a point of local maximum nor a point of local minimum of the function f.
Note 3. The theorem holds if c is an interior point of I.
Let a function f be defined on [0, 1] by f(x) = x, x ∈ [0, 1]. Then f has a local maximum at 1 (not an interior point of I), f is differentiable at 1, but f’(1) ≠ 0.
Theorem : (First derivative test for extrema)
Let f be continuous on I = [a, b] and c be an interior point of I. Let f be differentiable on (a, c) and (c, b).
- If there exists a neighbourhood (c - δ, c + δ) ⊂ I such that f’(x) ≥ 0 for x ∈ (c - δ,c) and f'(x) ≤ 0 for x ∈ (c, c + δ), then f has a local maximum at c.
- If there exists a neighbourhood (c - δ, c + δ ) ⊂ I such that f’(x) ≤ 0 for x ∈ (c - δ,c) and f(x) ≥ 0 for x ∈ (c, c + δ), then f has a local minimum at c.
- If f (x) keeps the same sign on (c - δ.c) and (c .c + δ), then f has no extremum at c.
Proof. 1. Let x ∈ (c - δ, c). Applying Mean value theorem to the function f on [x, c], we have f(c) - f(x ) = (c - x) f'(ξ) for some x ∈ (x, c).
Since f'(ξ) ≥ 0, we have f(x) ≤ f(c) for x ∈ (c - δ, c).
Let x ∈ (c, c + δ). Applying Mean value theorem to the function f on [c, x], we have f(x) - f(c) = (x - c)f'(η) for some η ∈ (c, x).
Since f’(η) ≤ 0. we have f(x) ≤ f(c) for x ∈ (c, c + δ).
If follow that f(c) ≥ f(x) for all x ∈ N(c, δ) ∩ I.
Therefore f has a local maximum at c.
2. Similar proof.
3. Let f’(x) > 0 for x ∈(c - δ, c) and for x ∈ (c, c + δ).
Then f(x) < f(c) for x ∈ (c - 8, c) and f(c) < f(x) for x ∈ (c, c + δ).
Therefore f has neither a maximum nor a minimum at c.
Similar proof if f ’(x) < 0 for x ∈ (c - δ, c) and for (c, c + δ).
Note. The converse of the theorem is not true.
For example, let f(x) = 2x2 + x2 sin(1/x), x ≠ 0
= 0, x = 0.
Then f has a local minimum at 0.
f'(x) = 4x + 2x sin 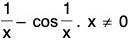
= 0, x = 0. f' takes both positive and negative values on both sides of 0 (in the immediate neighbourhood).
Examples:
- Let f(x) = I x I, x ∈

f is continuous on . f is not differentiable at 0.
. f is not differentiable at 0.
f’(x) < 0 for x ∈ (-δ, 0) and f’(x) > 0 for x ∈ (0, δ) for some δ > 0.
Therefore f has a local minimum at 0. - Let f(x) = |x - 1| + |x - 2|, x ∈ [0, 3]
Then f(x) = 3 - 2x, if 0 ≤ x < 1
= 1 , if 1 ≤ x ≤ 2
= 2x - 3, if 2 < x ≤ 3.
f is continuous on [0, 3]. f is not differentiable at 1 and 2.
f’(x) < 0 for x ∈ (1 - δ, 1), f'(x) = 0 for x ∈ (1, 1 + 8) for some δ satisfying 0 < δ < 1. Therefore f has a local minimum at 1.
f’(x) = 0 for x ∈ (2 - 8, 2), f’(x) > 0 for x ∈ (2 , 2 + 8) for some δ satisfying 0 < δ < 1.
Therefore f has a local minimum at 2. - f(x) = (x - 1)2 (x - 3)3, x ∈ R.
f'(x) = 2(x - 1)(x - 3)3 + 3(x - 1)2 (x - 3)2
= (x - 1)(x - 3)2 (5x - 9), x ∈ R.
f is continuous on R. f(x) = 0 at the points 1, 3, 9/5.
f’(x) > 0 for x ∈ (1 - δ, 1) and f'(x) < 0 for x ∈ (1, 1 + δ) for some δ > 0. Therefore f has a local maximum at 1.
f’(x) > 0 for x ∈ ( 3 - δ, 3) and f'(x) > 0 for x ∈ (3, 3 + δ) for some δ > 0. Therefore f has neither a maximum nor a minimum at 3.
f’(x) < 0 for x ∈ and f’(x) > 0 for x ∈
and f’(x) > 0 for x ∈  for some δ > 0. Therefore f has a local minimum at 9/5.
for some δ > 0. Therefore f has a local minimum at 9/5.
Theorem : (Higher order derivative test for extrema)
Let f : I → R and c be an interior point of I.
If f'(c) = f(c) = ... = fn-1 (c) = 0 and fn(c) ≠ 0, then f has
(i) no extremum at c if n be odd, and
(ii) a local extremum at c if n be even:
a local maximum if fn(c) < 0, a local minimum if fn(c) > 0.
Example :
- f(x) = x5 - 5x4 + 5x3 + 10, x ∈ R.
Show that f has a maximum at 1 and a minimum at 3 and f has neither a maximum nor a minimum at 0.
For an extremum f’(x) = 0. f'(x) = 0 at x = 1, 3, 0.
f”(x) = 20x3 - 60x2 + 30x. Therefore f”(1) < 0, f"(3) > 0, f"(0) = 0.
Since f’(1) = 0 and f"(1) < 0, f has a local maximum at 1.
Since f’(3) = 0 and f"(3) > 0, f has a local minimum at 3.
Since f’(0) and f"(0) = 0, in order to decide the nature of f at 0, we are to examine derivative of higher order at 0.
f”(x) = 60x2 - 120x + 30. f”(0) = 30 ≠ 0.
Therefore f has neither a maximum nor a minimum at 0. - Find the local extremum point of the function f(x)


f’(x) = 0 at x = -2, 0.
Let h be an arbitrarily small positive number.
f’( - 2 - h) > 0, f'(-2) = 0, f'(-2 + h) < 0.
f’(0 - h) < 0, f'(0) = 0, f'(0 + h) > 0.
f is continuous at - 2. f'(x) > 0 for x ∈ (- 2 - δ, 2) and f (x) < 0 for x ∈ (-2, -2 + δ) for some δ > 0.
f is continuous at 0.f’(x) < 0 for x ∈ (-δ, 0) and f’(x) > 0 for x ∈ (0, δ) for some δ > 0. Hence f has a local maximum at -2 and a local minimum at 0. - Find the global maximum and the global minimum of the function f on R, where f(x) =


f’(x) = 0 at x = ±2. f'(x) < 0 for |x| < 2 and f'(x) > 0 for |x| > 2.
f is continuous at 2. f’(2 + h) > 0 and f'(2 - h) < 0 for sufficiently small h > 0. Therefore f has a local minimum at 2 and f(2) = 1/3.
f is continuous at - 2. f'(-2 + h) < 0 and f‘(- 2 - h) > 0 for sufficiently small h > 0. Therefore f has a local maximum at -2 and f(-2) = 3.
As f'(x) > 0 for x > 2 and f is continuous at 2, f is an increasing function [2, ∞) and f(x) = 1.
f(x) = 1.
Therefore
As f’(x) > 0 for x < - 2 and f is continuous at - 2, f is an increasing function on (-∞, - 2] and
Therefore

Therefore
Example : Find the maximum and minimum points of the function f given by
f(x) = (x - 1) (x - 2) (x - 3).
f(x) = x3 - 6x2 + 11 x - 6
f’(x) = 3x2 - 12x + 11
f”(x) = 6x - 12
For maximum or minimum,
f'(x) = 0 ⇒ 3x2 - 12x + 11 = 0
⇒
At
⇒ f is minimum at x = 2
At x = 2 -
⇒ f is minimum at x = 2 -
Example : Show that x5 - 5x4 + 5x3 - 1 has a maximum when x = 1, a minimum when x = 3 and neither when x = 0.
Let f(x) = x5 - 5x4 + 5x3 - 1
f’(x) = 5x4 - 20x3 + 15x2
f”(x) = 20x3 - 60x2 + 30x
For maximum or minimum.
f’(x) = 0 ⇒ 5x2(x2 - 4x + 3) = 0
⇒ x2(x - 1) (x - 3) = 0 x = 0, 1, 3
At x = 0, f”(x) = 0
Since f"(x) = 60x2 - 120x + 30, f”(0) = 30 ≠ 0
⇒ f has neither a max. nor mini, when x = 0
At x = 1, f”(x) = 20 - 60 + 30 = -10 < 0
⇒ f has a maximum when x = 1
At x = 3, f”(x) = 20(3)3 - 60(3)2 + 30(3) = 90 > 0
⇒ f has a minimum when = 3.
Example : Examine the following function for extreme values : (x - 3)5 (x + 1)4.
Let f(x) = (x - 3)5 (x + 1)4
then f(x) = (x - 3)5. 4(x + 1)3 + 5(x - 3)4 (x + 1)4
= (x - 3)4 (x + 1)3 [4(x - 3) + 5(x + 1)] = (x - 3)4 (x + 1)3 (9x - 7)
For maximum or minimum,
f(x) = 0 ⇒ x = 3, - 1, 7/9
Let us test values one by one.
(i) For x slightly < 3, f’(x) = (+)(+)(+) = +ve
For x slightly > 3, f’(x) = (+)(+)(+) = +ve
Since f’(x) does not changes sign as a passes through 3, f is neither maximum nor minimum at x = 3.(ii) For x slightly < -1, f'(x) = (+)(-)(-) = +ve
For x slightly > - 1, f'(x) = (+)(+)(-) = - ve
Since f’(x) changes sign from +ve to -ve as x passes through -1, f is maximum at x = -1
fmax = f(-1) = 0
(iii) For x slightly < 7/9, f’(x) = (+)(+)(-) = -ve
For x slightly > 7/9, f’(x) = (+)(+)(+) = +ve
Since f’(x) changes sign from -ve to +ve as x passes through 7/9, f is minimum at x = 7/9
Example : Find the maximum and minimum values, if any, of the function (1 - x)2 ex.
Let f(x) = (1 - x)2 ex
f(x) = (1 - x)2 . ex - 2(1 - x)ex
= (1 - x)(1 - x - 2) ex = (1 - x)(-1 -x) ex
= (x + 1)(x - 1) ex = (x2 - 1) ex
f”(x) = (x2 - 1).ex + 2x . ex = (x2 + 2x - 1) ex
For maximum or minimum, f'(x) = 0
⇒ (x2 - 1)ex = 0 ⇒ x2 - 1 = 0 [∵ ex ≠ 0 for any x ∈ R]
∴ x = ± 1
When x = 1, f”(x) = 2e > 0 ⇒ f is minimum at x = 1
fmin = f(1) = 0
When x = - , f"(x) = -2e-1 < 0 f is maximum at x = -1
fmax = f(-1) = 4e-1 = 4/e.
Example : Find the maximum value of (logx/x), 0 < x < ∞.
Let f(x) = logx/x
then
For maximum or min., f(x) = 0 ⇒ 1 - log x = 0
⇒ log x = 1 = log e ⇒ x = e
When x = e,
⇒ f is maximum at x = e.
Example : Prove that the function (1/x)x, x > 0 has a maximum at x = 1/e.
Let
∴
∴
For max. (or min.) f(x) = 0 ⇒ - f(x) [1 + log x] = 0
⇒ 1 + log x = 0 [∵ f(x) ≠ 0]
⇒ log x = - 1 ⇒ x = e-1
Also f”(e-1) = -f(e-1) . e - f(e-1)[1 + log e-1] = - (e)1/e. e - 0 < 0 [∵ f’(e-1) = 0]
⇒ f is maximum at x = e-1 = 1/e.
Example : Show that sin x(1 + cos x) is a maximum when x = π/3.
Let f(x) = sin x(1 + cos x)
then f'(x) = sin x(- sin x) + cos x(1 + cos x)
= cos2 x - sin2 x + cos x = cos 2x + cos x
f”(x) = -2 sin 2x - sin x
For max. or min., f(x) = 0
⇒ cos 2x + cos x = 0 ⇒
⇒ either
Here we have to consider only the point x = π/3
⇒ f(x) has a maximum at x = π/3.
Example: Find the maximum and minimum values of the function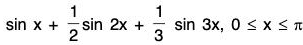
Let
then f'(x) = cos x + cos 2x + cos 3x
f"(x) = - [sin x + 2 sin 2x + 3 sin 3x]
For max. or min., f’(x) = 0
⇒ cos x + cos 2x + cos 3x = 0 ⇒ (cos 3x + cos x) + cos 2x = 0
⇒ 2 cos 2x cos x + cos 2x = 0 ⇒ cos 2x(2 cos x + 1) = 0
⇒ either cos 2x = 0 or cos x = -(1/2)
⇒
When
⇒ f is maximum at x = π/4
When x =
⇒ f is maximum at x = 2π/3
When
⇒ f is maximum at x = 3π/4
Example : Prove that the function f(0) = sinp θ cosq θ has a maximum at q = tan-1
f(θ) = sinp θ cosq θ
f’(θ) = sinp θ . θ cosq-1 θ (- sin θ) + p sinp-1 θ (cos θ) cosq θ
= - q sinp-1 θ cosq-1 θ + p sinp - 1 θ cos q+1 θ
= sinp-1 θ cosq-1 θ(p cos2 θ - q sin2 θ)
For maxima or minima, f(θ) = 0
⇒ sin θ = 0 or cos θ = 0 or p = cos2 θ = q sin2 θ
⇒
Also f"(θ) = sinP-1 θ cosq-1 θ (p cos2θ - q sin2θ)
∴ f"(θ) = f(θ) [ - p cosec2θ - q sec2θ] + f’(θ) (p cot θ - q tan θ)
At θ
∴ f”(θ) = -f(θ) [p cosec2 θ + q sec2 θ] at θ = tan-1which is negative
Hence f(θ) is maximum at θ =
Indeterminate forms and L'Hospital's Rule
Theorem : (L’Hospital’s Rule) : Suppose f and g are differentiable and g’(x) ≠ 0 near a (except possible at a). Suppose that 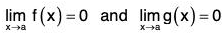
or that 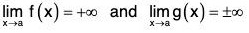
(In other words, we have an indeterminate form of type 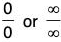 ). Then
). Then
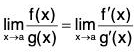 if the limit on the right side exists (or is ∞ or -∞).
if the limit on the right side exists (or is ∞ or -∞).
Indeterminate Forms of Type 
Example: Find 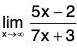
We have
In short,
Example : Find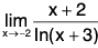
We have

In short,
Example : Find 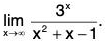
We have
Example: Find 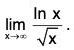
We have
Example : Find 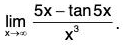
We have
Sinceis an indeterminate form of type 0/0, we can use L’Hospital’s Rule again. But it is easier to do trigonometry instead. Note that 1 - sec2 5x = - tan2 5x. Therefore
Example : Find 
One can show, however, thatdoes not exist. In fact, we first note that 1 + cos x and 1 - sin x may attain any value between 0 and 2. From this one can deduce that
attains any nonnegative value infinitely often as x → ∞. This means that
does not exist, so L’Hospital’s Rule can’t be applied here.
Example : Find 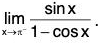
We have
The is WRONG. In fact, although the numerator sin x → 0 as x → π-, notice that the denominator (1 - cos x) does not approach 0, so L’Hosptial Rule can’t be applied here. The required limit is easy to find, because the function is continuous at n and the denominator is nonzero here:
Example : Find 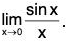
We have
Indeterminate Forms of Type ∞ - ∞ and 0 • ∞
Example : Find 
We have
Note that
thereforeOR
Example : Find 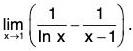
We have
Example : Find 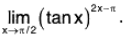
Note that
type of an indeterminate form. Put y = (tan x)2x-n
then
In y = In ((tan x)2x-π) = (2x - π) ln(tan x)
We have
Therefore
Example : Find 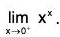
In short, y = xx ⇒ In y = x In x =
We have
Therefore
Example : Find 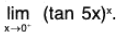
Note that
(tan 5x)x is 0° type of an indeterminate form. Put y = (tan 5x)x
then
In y = ln(tan 5x)x = x ln(tan 5x) =
We have
Therefore
Example : Find 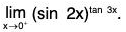
Note that
is 00 type of an indeterminate form. Put y = (sin 2x)tan 3x
then In y = ln((sin 2x)tan 3x) = tan 3x ln(sin 2x) =
We have
Therefore
Example : Find 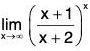
Note that
is 1∞ type of an indeterminate form. Put y =
then
In y = In
We have
Therefore,
Example : Find 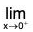 (1 + sin 7x)cot.5x.
(1 + sin 7x)cot.5x.
Note that
is 1∞ type of an indeterminate form. Put y = (1 + sin 7x)cot 5x
then
In y = ln((1 + sin 7x)cot 5x) = cot 5x ln(1 + sin 7x) =
We have
Therefore
|
98 videos|27 docs|30 tests
|
FAQs on Functions of One Variable - II - Mathematics for Competitive Exams
| 1. What is Rolle's Theorem? |  |
| 2. What is the Mean Value Theorem? |  |
| 3. What is Taylor's Theorem? |  |
| 4. How do you find the maxima and minima of a function? |  |
| 5. What are indeterminate forms and how does L'Hospital's Rule help with them? |  |

|
Explore Courses for Mathematics exam
|

|
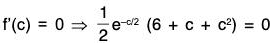
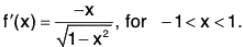
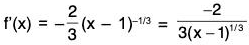

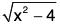 s an algebraic function of x, so f is continuous in [2, 4]. Also f is derivable in ]2, 4[.
s an algebraic function of x, so f is continuous in [2, 4]. Also f is derivable in ]2, 4[.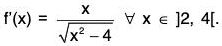
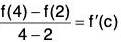
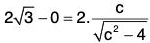
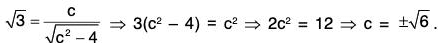
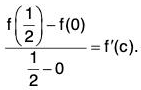 ...(1)
...(1)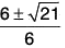
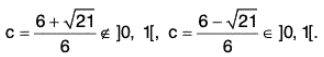
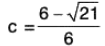 and the theorem is verified.
and the theorem is verified.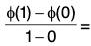 φ’(θ) or φ(1) - φ(0) = φ’(θ).
φ’(θ) or φ(1) - φ(0) = φ’(θ).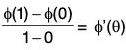 for some θ ∈ ]0, 1[
for some θ ∈ ]0, 1[ 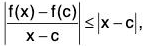 using (1).
using (1).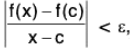 when |x - c| < δ.
when |x - c| < δ.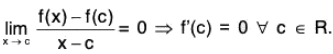
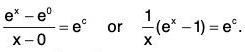 ...(1)
...(1)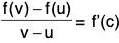 for some c ∈ ] u, v [
for some c ∈ ] u, v [ for u < c < v. ...(1)
for u < c < v. ...(1)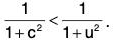 ...(2)
...(2)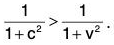 ...(3)
...(3)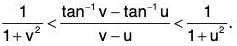
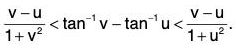 ...(4) (∵ u < v ⇒ v - u > 0)
...(4) (∵ u < v ⇒ v - u > 0)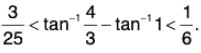

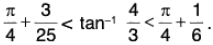
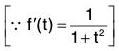
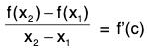 for some c ∈ ]x1, x2[
for some c ∈ ]x1, x2[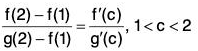
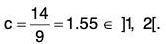
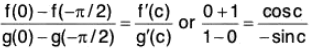
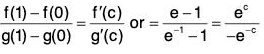
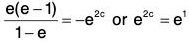
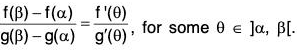
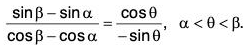

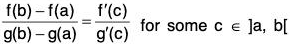
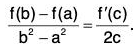
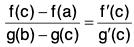
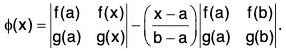 ...(1)
...(1)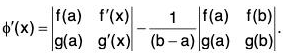
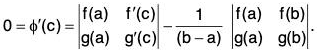
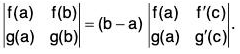
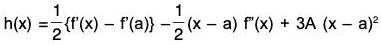 ...(3)
...(3)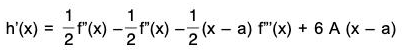
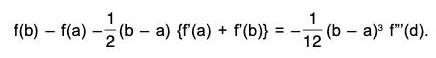
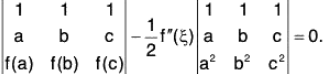 ...(2)
...(2)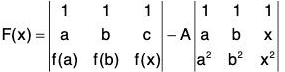 ...(3)
...(3)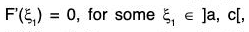

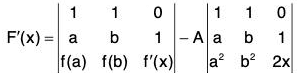 ...(6)
...(6)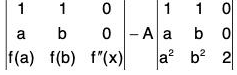
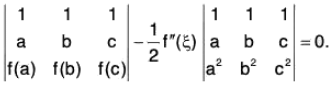
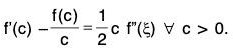
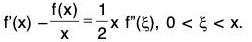
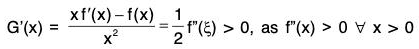
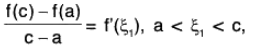
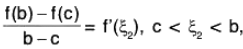 respectively.
respectively.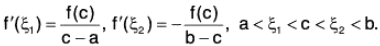 ...(1)
...(1)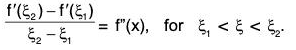 ...(2)
...(2)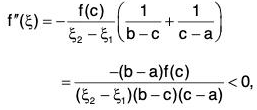
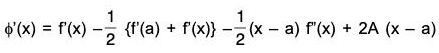
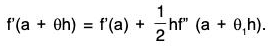 ...(3)
...(3)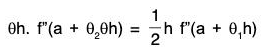
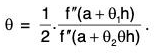
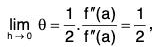 since f" continuous in [a, a + h].
since f" continuous in [a, a + h].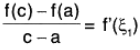 for some ξ1 ∈ ]a, b[,
for some ξ1 ∈ ]a, b[, for some ξ2 ∈ ]c, b[,
for some ξ2 ∈ ]c, b[,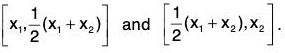 Consequently,
Consequently,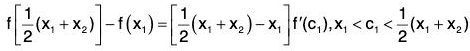
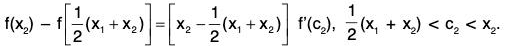
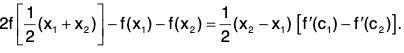 ...(2)
...(2)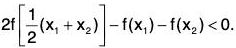
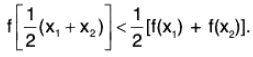
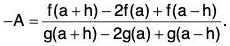 ...(5)
...(5)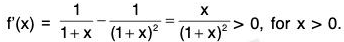
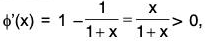 for x > 0.
for x > 0.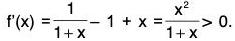 (∵ x > 0)
(∵ x > 0)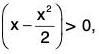 for x > 0
for x > 0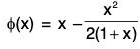 - log(1 + x), so that φ(0) = 0.
- log(1 + x), so that φ(0) = 0.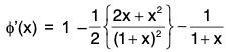
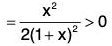 (∵ x > 0)
(∵ x > 0)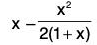 - log (1 + x) > 0, for x > 0
- log (1 + x) > 0, for x > 0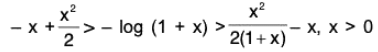
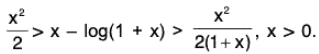
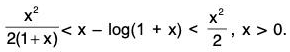
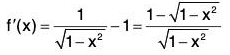
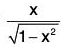 - sin-1 x, so that g(0) = 0.
- sin-1 x, so that g(0) = 0.
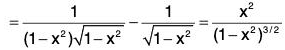
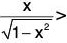 sin-1 x, for 0 < x < 1
sin-1 x, for 0 < x < 1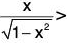 , for 0 < x < 1.
, for 0 < x < 1.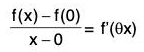 (∵ ]0, x [ = ]0 x , 1 x [, c = θx)
(∵ ]0, x [ = ]0 x , 1 x [, c = θx)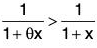
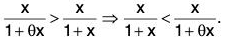 ...(2)
...(2)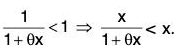 ...(3)
...(3)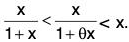 ...(4)
...(4)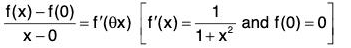
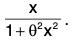 ...(1)
...(1) ...(2)
...(2)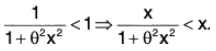 ...(3)
...(3)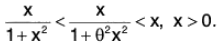 ...(4)
...(4)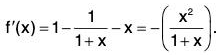 ...(1)
...(1)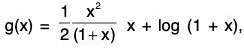 so that g(0) = 0.
so that g(0) = 0.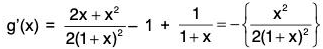
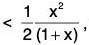 -1 < x < 0
-1 < x < 0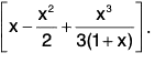
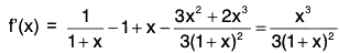
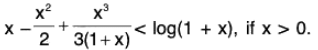
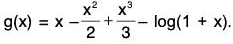
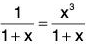

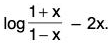
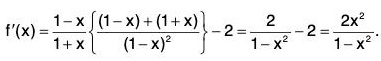
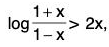 for 0 < x < 1.
for 0 < x < 1.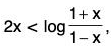 for 0 < x < 1.
for 0 < x < 1.
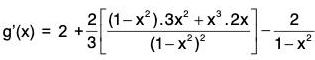
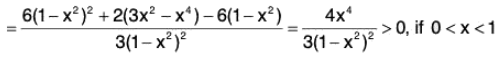
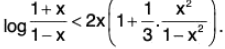
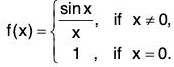 ...(1)
...(1)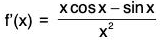 ...(2)
...(2)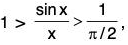 using (1)
using (1)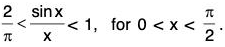
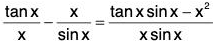
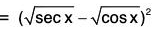 + 2 sin2 x sec3 x.
+ 2 sin2 x sec3 x.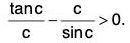
 whenever 0 < x < π/2.
whenever 0 < x < π/2.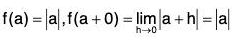
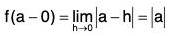


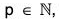 Then ∃ θ ∈ (0, 1) such that
Then ∃ θ ∈ (0, 1) such that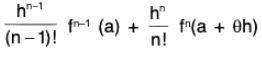 where 0 < θ < 1.
where 0 < θ < 1.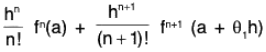 where 0 < θ1 < 1
where 0 < θ1 < 1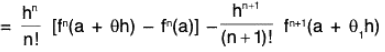
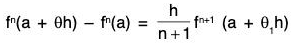 ...(1)
...(1)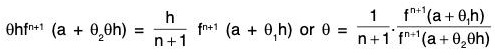
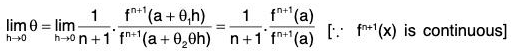
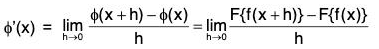
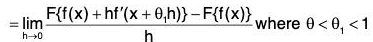 [∵ f(x + h) = f(x) + hf'(x + θ1h) by Mean Value Theorem]
[∵ f(x + h) = f(x) + hf'(x + θ1h) by Mean Value Theorem]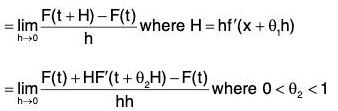
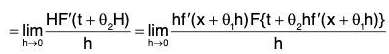
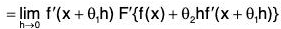

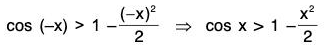
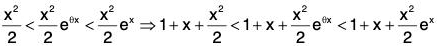
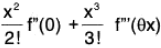 where 0 < θ < 1
where 0 < θ < 1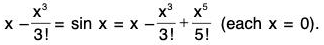
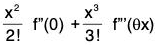
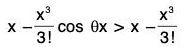

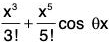
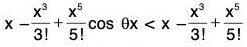
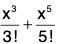 ...(2)
...(2)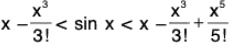
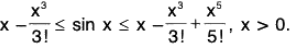
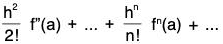
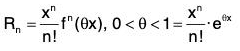

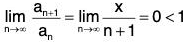
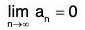
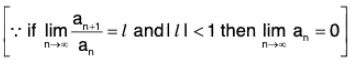

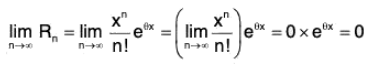
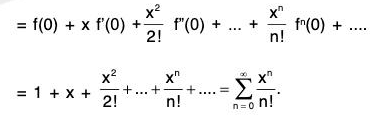
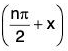


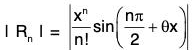
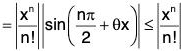
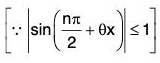
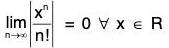
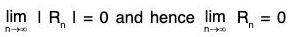
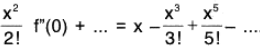
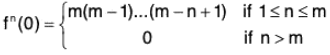
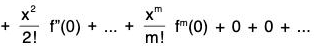
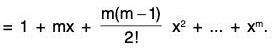
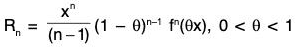
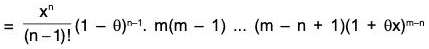
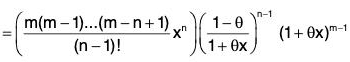
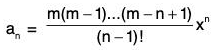
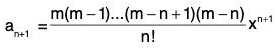
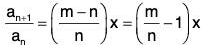
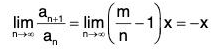
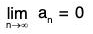
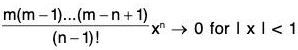 ...(1)
...(1)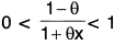
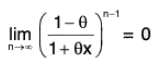 ...(2)
...(2)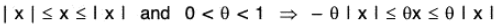
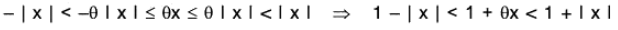
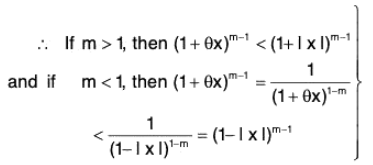 ...(3)
...(3)

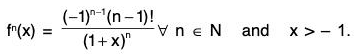
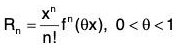
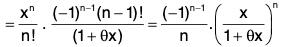
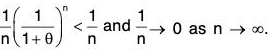

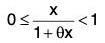 ⇒
⇒ 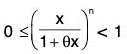
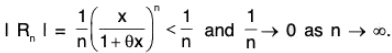
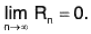
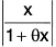 need not be less than unity, therefore, it may not be easily shown that Rn → 0 as n → ∞ by considering Lagrange’s remainder.
need not be less than unity, therefore, it may not be easily shown that Rn → 0 as n → ∞ by considering Lagrange’s remainder.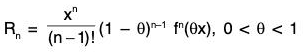
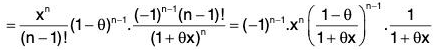
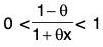

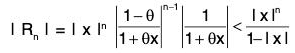

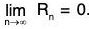
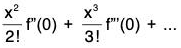
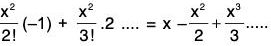
 . f is not differentiable at 0.
. f is not differentiable at 0.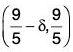 and f’(x) > 0 for x ∈
and f’(x) > 0 for x ∈ 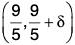 for some δ > 0. Therefore f has a local minimum at 9/5.
for some δ > 0. Therefore f has a local minimum at 9/5.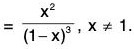
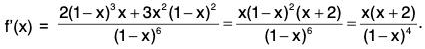
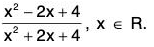
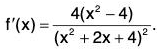
 f(x) = 1.
f(x) = 1.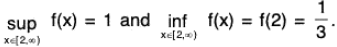

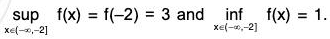
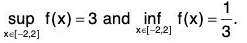
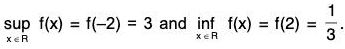
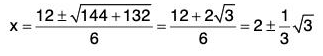
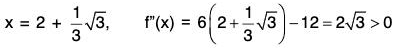
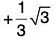
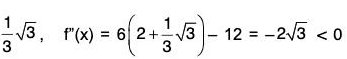

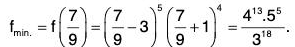
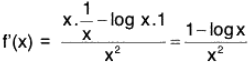
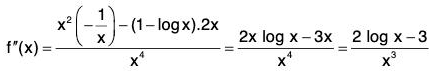
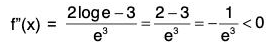
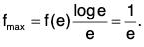
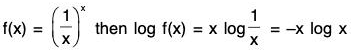
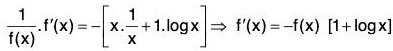
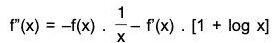
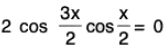

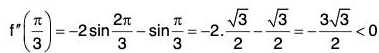
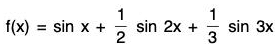
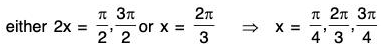
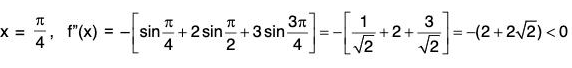

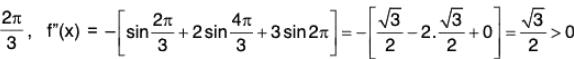
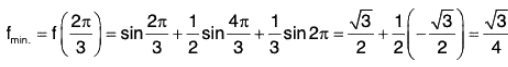
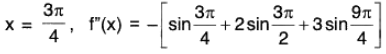
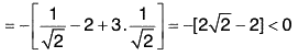
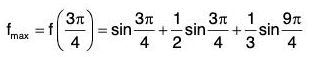
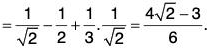
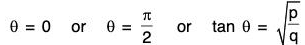
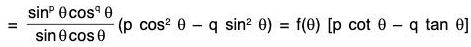
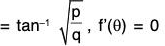
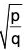 which is negative
which is negative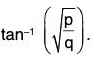
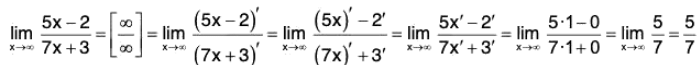
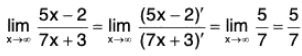
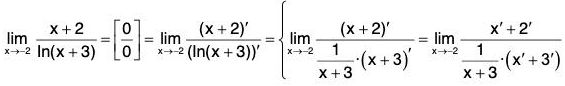
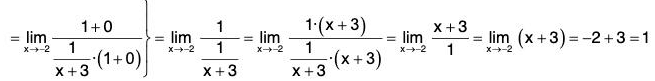
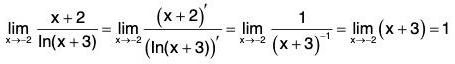
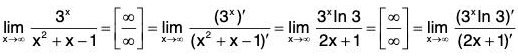
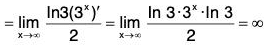
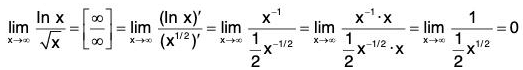
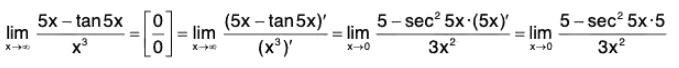
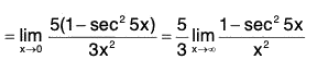
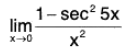 is an indeterminate form of type 0/0, we can use L’Hospital’s Rule again. But it is easier to do trigonometry instead. Note that 1 - sec2 5x = - tan2 5x. Therefore
is an indeterminate form of type 0/0, we can use L’Hospital’s Rule again. But it is easier to do trigonometry instead. Note that 1 - sec2 5x = - tan2 5x. Therefore 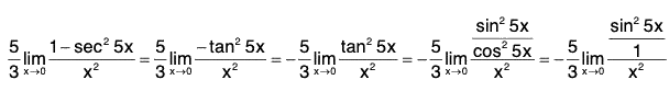
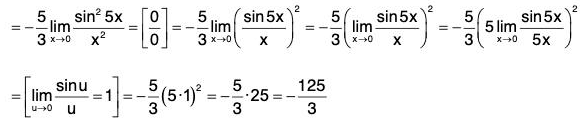
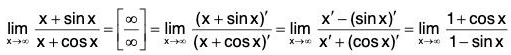
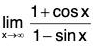 does not exist. In fact, we first note that 1 + cos x and 1 - sin x may attain any value between 0 and 2. From this one can deduce that
does not exist. In fact, we first note that 1 + cos x and 1 - sin x may attain any value between 0 and 2. From this one can deduce that 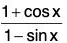 attains any nonnegative value infinitely often as x → ∞. This means that
attains any nonnegative value infinitely often as x → ∞. This means that 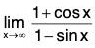 does not exist, so L’Hospital’s Rule can’t be applied here.
does not exist, so L’Hospital’s Rule can’t be applied here.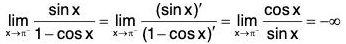
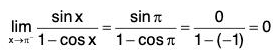
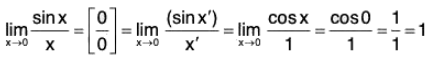
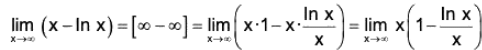
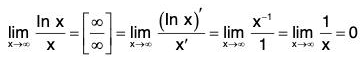
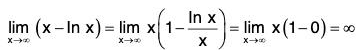
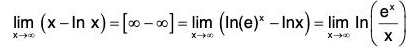
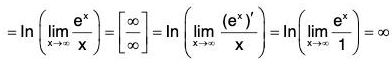
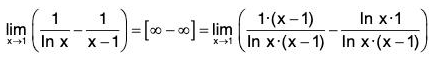
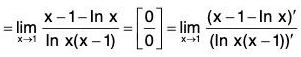
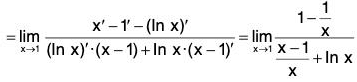
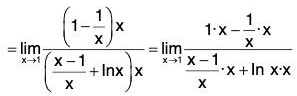
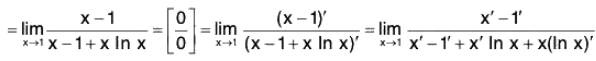
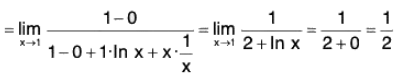
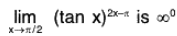 type of an indeterminate form. Put y = (tan x)2x-n
type of an indeterminate form. Put y = (tan x)2x-n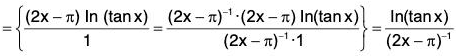
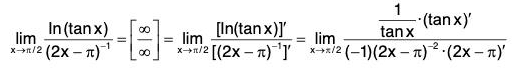
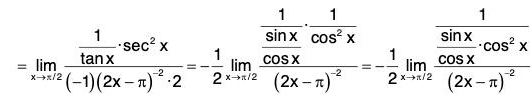
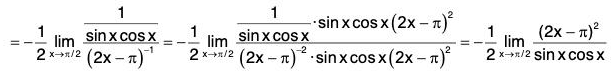
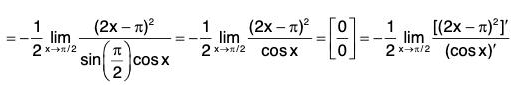
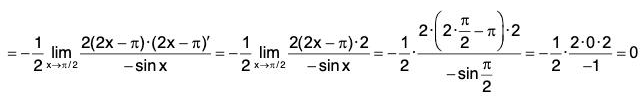
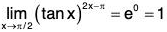
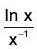
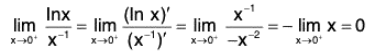
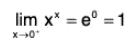
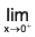 (tan 5x)x is 0° type of an indeterminate form. Put y = (tan 5x)x
(tan 5x)x is 0° type of an indeterminate form. Put y = (tan 5x)x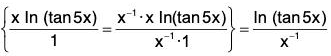
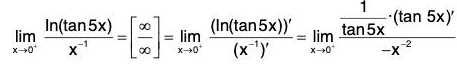
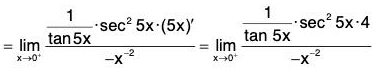
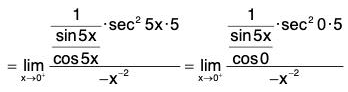
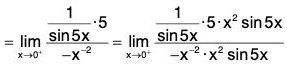
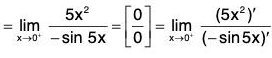
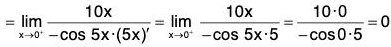
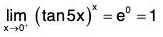
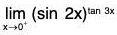 is 00 type of an indeterminate form. Put y = (sin 2x)tan 3x
is 00 type of an indeterminate form. Put y = (sin 2x)tan 3x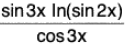
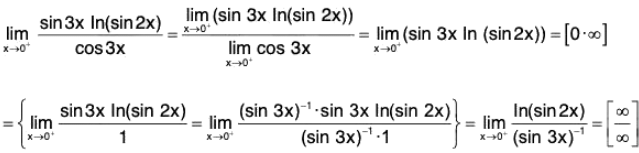
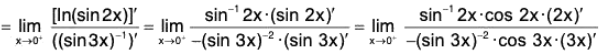
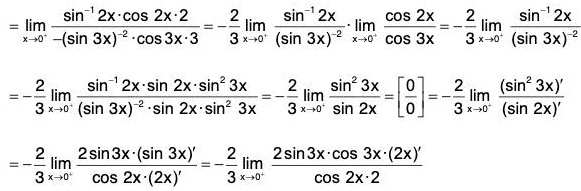

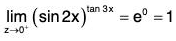
 is 1∞ type of an indeterminate form. Put y =
is 1∞ type of an indeterminate form. Put y = 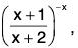 then
then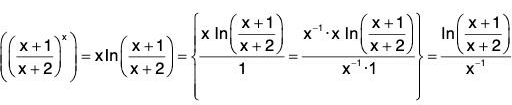
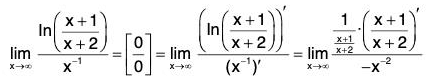
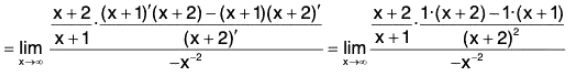
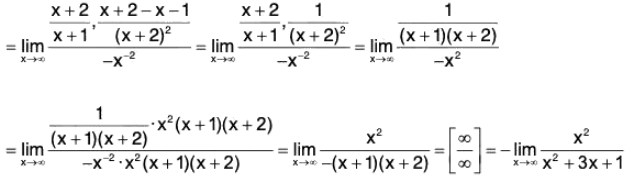
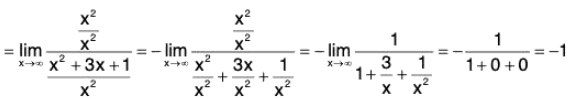
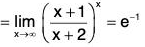
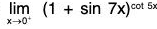 is 1∞ type of an indeterminate form. Put y = (1 + sin 7x)cot 5x
is 1∞ type of an indeterminate form. Put y = (1 + sin 7x)cot 5x