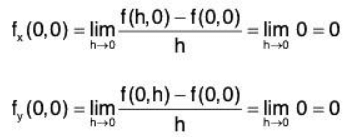Functions of Two or Three Variables- I | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Introduction |

|
| Limit of a Function of Two Variables |

|
| Continuity of a Function of Two Variables |

|
| Partial Derivatives |

|
| Differentiability of Two Variables |

|
Introduction
Functions of Two Variables
One of the main differences between functions of one variable and functions of two variables is that functions of one variable are considered in an interval on the number line, whereas functions of two variables are considered in an open disc in the xy-plane. That is, with a function of one variable, |x - a|<δ means that within an interval, the distance of δ to a is always less than 5. With a function of two variables, 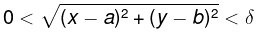 means that the point (a, b) lies within an open circle (disc) whose radius is δ or denoted as
means that the point (a, b) lies within an open circle (disc) whose radius is δ or denoted as 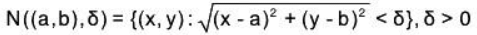 read as neighborhood (nbd) of (a, b).
read as neighborhood (nbd) of (a, b).
Sometimes we can also take an open rectangle centered at (a,b)
{(x,y) :|x-a|< h,|y-b|<k}, (h > 0, k > 0)
This is denoted as (a - h, a + h ; b - k, b + k).
Definition: A function of 2 variables is a rule that assigns to each ordered paired of real numbers (x, y) in a set D a unique real number denoted by f(x, y). The set D is the domain of f and its range is the set of values that f takes on, i.e., the set {f(x, y)l(x, y) ϵ D}.
Remark: We often write z = f(x, y). D ⊂ R2 and the range is a subset of
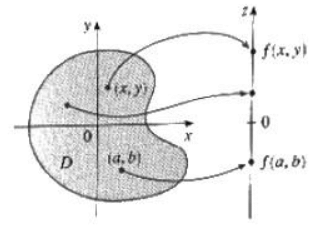
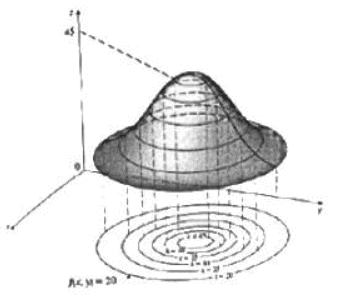
➤ Level Curves
Definition: The level curves (or contour lines) of a function f(x, y) are the curves with equations f(x, y) = k where k is a constant in the range of f.
Limit of a Function of Two Variables
Definition. Let f : D →R,
The function f(x, y) has a limit l (l ∈ R) as (x, y) tends to (a, b) ∈ R2, written as 
if given any ε > 0, there exists some δ > 0, such that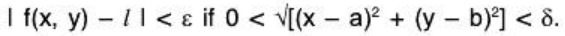
Equivalently,
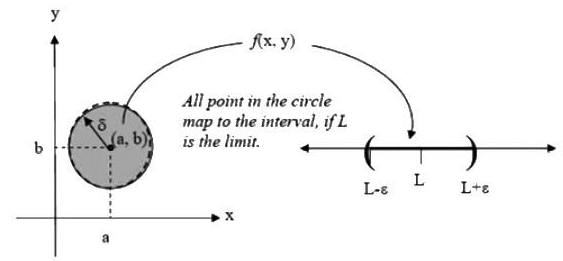
Note: In the above definition, the function f may or may not be defined at the point (a, b).
➤ Repeated Limits
Let f : D → R, D If 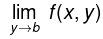 exists, then it is a function of x say h(x), which is defined on some subset of R. If
exists, then it is a function of x say h(x), which is defined on some subset of R. If 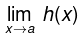 exists, then we say that the repeated limit
exists, then we say that the repeated limit 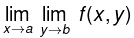 exists. Similarly we can define the repeated limit
exists. Similarly we can define the repeated limit 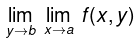
➤ Remarks
- Repeated limits may exist but may not be equal.
- Repeated limits may exist and be equal but the two-variable limit may not exist.
- Repeated limits and the two-variable limit may all exist and may be equal.
- Repeated limits may not exist but the two-variable limit may exist.
Note: To find the limit of a function of one variable, we only needed to test the approach from the left as well as from the right. If both approaches were the same, the function had a limit. To find the limit of a function of two variables however, we must show that the limit is the same no matter from which direction we approach (a,b)
Example
The function f defined by
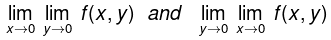 both exist but are unequal. Also show that
both exist but are unequal. Also show that
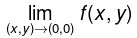 does not exist.
does not exist.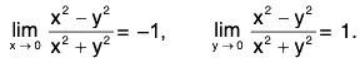
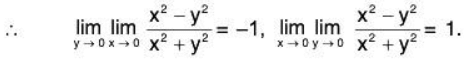
Thus the two repeated limits exist but are unequal.
Suppose (x, y) → (0, 0) along the path y = mx.
Now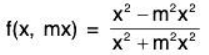
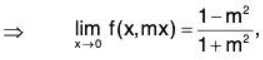
which is different for different values of m.
Hence 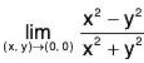 does not exist.
does not exist.
Example 1: Find the limit.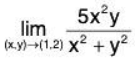
Notice that the point (1,2) does not cause division by zero or other domain issues. So,

Example 2: Find the limit.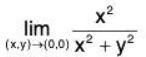
approaching (0,0) along x=0 i.e. y- axis
as x = 0
Similarly, approaching (0,0) along y=0 i.e. x- axis
as y = 0
Since we got two different results, the limit does not exist.
Example 3: Find the limit.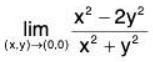
Let x = 0: then
Now let y = 0; then
Again, the limit does not exist.
Example 4: Find the limit.
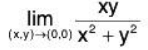
Let (x.y) → (0 ,0) a long the line y = mx.
then
This shows that the limit depends on the choice of m. Therefore, the limit does not exist.NOTE: When we use the definition of limit to show that a particular limit exists, we usually employ certain key or basic inequalities such as:

and the algebraic terms.
Example 5: Using ε - δ definition of limit, prove that: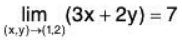
Given ε > 0, we shall show that there exist δ > 0 such that
Now by the triangle inequality,
I3x + 2y - 7| = |5x - 3 + 2y - 4| < I3x - 3| + |2y - 4| = 3|x - 1| + 2|y - 2|
Since
and
Therefore
Now let
Therefore δ exists.
Hence
Example 6: Using ε - δ definition of limit, prove that: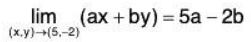
Given ε > 0, we shall show that there exist δ > 0 such that
Now by the triangle inequality
l(ax + by) - (5a - 2b)| = |a(x - 5) + b(y + 2) < alx - 5| + b|y + 2|
Clearly,
∴ l(ax + by) - (5a - 2b) < alx - 5| + b|y + 2| < aδ + bδ = (a + b)δ
Now choose
Therefore δ exists.
Hence
Example 7. Using ε - δ technique, prove that: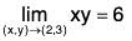
Given ε > 0, we shall show that there exist δ > 0 such that
Now by the triangle inequality,
Ixy - 6| = |xy - 3x + 3x - 6| = |x(y - 3) + 5(x - 2)| < Ixl ly - 3| +3|x - 2|
Clearly,
Now choose δ = 1,
lx - 2| < 1 ⇒ 1 < x < 3 ⇒ 1 < Ixl < 3
Therefore
Ixy - 6| ≤ Ixlly - 3 | + 3|x - 2| < 3ly - 3| + 3|x - 2| < 3δ + 3δ = 6δ
Therefore, for δ = (ε/6), Ixy - 6| < 6. (ε/6) = δ
Therefore δ exists.
Hence
Example 8: Using ε - δ technique, prove that: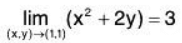
Given ε > 0, we shall show that there exist δ > 0 such that
Now by the triangle inequality,
|x2 + 2y-3 | = |x2 - 1 + 2y - 2| = |x2-1+2(y-1)|
≤ |x2 - 1| + 2 |y - l|
≤ |x - l||x + l| + 2 |y - l|
Clearly,
Now choose δ = 1,
lx — 1| < 1 ⇒ 0 < x < 2
⇒1 < x + 1 < 3 1 < lx + 11 < 3
lx2 + 2y - 3| < lx - 1| | x + 1| + 2|y - 1| < 3lx — 1| + 2|y - 1| < 3δ + 2δ = 5δNow choose δ = (c /5), |x2+2y-3| < (5ε / 5)<ε
Therefore required δ = min{1,(ε/5)} i.e., δ exists.
Hence
Continuity of a Function of Two Variables
Definition : Let f : D → R
Then f is said to be continuous at a point (a, b) ∈ D if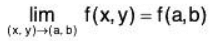
In other words, f is continuous at a point (a, b) ∈ D if given and ε > 0, there exists some δ > 0 such that
Example 1: Examine the following function for continuity at (0,0):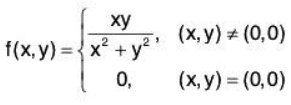
We know that if
exists, then this limit is independent of path of approach along which we approach the point (a, b).
Since f(x, y) is identically zero along the co-ordinates,
therefore when (x, y) -> (0, 0), then the limit along each axis is zero.
But the path of approach is along a straight line y = mx, where m ≠ 0,
thenwhich depends on m., i.e., the limit of the function depends on the path of approach.
Thereforedoes not exist.
Again if the path of approach be parabola x = y2, then
Since the limits obtained by two different approaches are different, sodoes not exist.
Hence the function f(x, y) is not continuous at the point (0,0).
Example 2: Examine for continuity the following function at (0,0):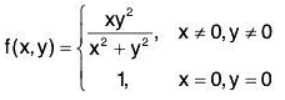
Given f(0,0) = 1 ....(1)
and....(2)
Since (1) ≠ (2)
Therefore the given function is discontinuous at (0,0).
Example 3: Show that the following function 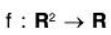 is continuous at (0,0):
is continuous at (0,0):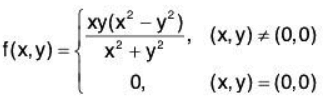
Let ε > 0 and |x - 0| < >√ε and |y - 0| < >√ε , then
i.eexists and equal to 0.
And value of the
Hence the given function is continuous at (0, 0).
Example 4: Show that the real valued function f(x,y) of two variables defined below is continuous at the origin: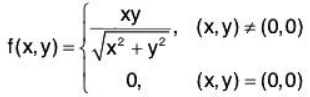
Let x = r cosθ, y = r sinθ and ε > 0,
then
Here if we take δ < ε/√2, then Ixl < δ and lyl < δ
Thus, for everysuch that
lf(x, y) - f(0 , 0 )| < ε whenever lx — 0 | <δ and ly - 0 | < δ
Therefore f is continuous at the origin (0,0).
Theorem: The following results are true for multivariable functions:
- The sum, difference and product of continuous functions is a continuous function.
- The quotient of two continuous functions is continuous as long as the denominator is not 0.
- Polynomial functions are continuous.
- Rational functions are continuous in their domain.
- If f(x,y) is continuous and g(x) is defined and continuous on the range of f, then g(f(x,y)) is also continuous.
Example 1: Show that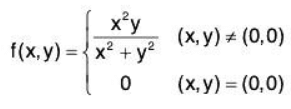
is continuous at (0,0).
This function is clearly continuous everywhere except at (possibly) (0,0). Let’s check continuity at (0,0)
Let ε > 0 be given. Let δ =ε/2 and suppose that
Then, using the fact thatwe have
Hence, f(x,y) is continuous at (0,0).
Example 2 : Show that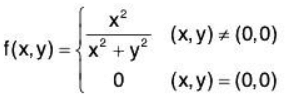
is discontinuous at (0,0).
Again this function is clearly continuous everywhere except (possibly) at (0,0). Now let’s look at the limit as (x, y) approaches (0, 0) along two different paths. First, let’s approach (0,0) along the x-axis, i.e. y = 0.
Now, let’s approach (0,0) along the y-axis, i.e. x = 0.
Since the limit is not the same along the two different directions we conclude that f(x, y) is discontinuous at (0, 0).
Partial Derivatives
If f(x) = 5x3, then f '(x) = 5 x 3x2 = 15x2. In the same way, if you’re given g(x) = ax3, and told that a is a constant, then you find that g’(x) = a-3x2 = 3ax2. If you are now told that a = 5, you can plug in 5 for a in this latter answer to get what you got before.
Suppose now that you’re given the function of two variables h(x,y) = yx3. Since y is one of the independent variables in h, clearly y is not intended to always be constant. However, if you’re told to assume that, for some physical or mathematical reason, y is held constant at the value y = 5, and asked to differentiate h as a function of x, you would look at h(x, 5) = 5x3, and differentiate, to once again obtain 15x3. If, instead, you’re told to assume that y is held constant at the value y = 7, and asked to differentiate h as a function of x, you would look at h(x, 7) = 7x3, and differentiate to obtain 21x3.
More generally, you could just be told to assume that y is held constant, without being told that the constant value is 5 or 7 or anything else specific; then, you can calculate the derivative of yx3, with respect to x, thinking of y as a constant; you find y.3x2.
This process of taking the derivative, with respect to a single variable, and holding constant all of the other independent variables, is called finding (or, taking) a partial derivative. This is a fundamental mathematical concept that arises in many contexts.
Definition: Suppose that we have a real-valued function z = f(x,y) of two real variables. Then, the derivative of f, with respect to x, holding y constant, is called the partial derivative of f, with respect to x, and is denoted by any of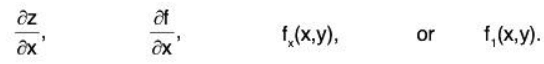
In the same way, the derivative of f, with respect to y. Holding x constant, is called the partial derivative of f, with respect to y, and is denoted by any of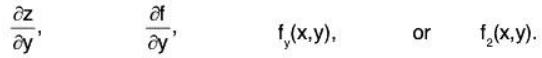
We also use the partial derivative operators: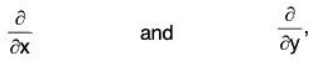
which tell you to take the partial derivative with respect to x and y, respectively.
We mention the notations f1(x.y) and f2(x,y) primarily because you may see them used in other books; there are also technical reasons why these notations are useful in some contexts. However, we shall avoid their use to indicate partial derivatives, since we like to reserve the notations f1(x.y) and f2(x,y) for use in denoting the component functions of a multi-component function f(x,y) = (f1,(x,y), f2(x,y). In any case, we will explicitly state, or the context will make clear, what we mean by f1, f2 or, more generally, fi.
Example 1: Consider the fairly simple function
z = f(x,y) = x2 - y2.
We first take the partial derivative, with respect to x, thinking of y as a constant. Let’s use all of our various notations just for practice. We find
Now, we take the partial derivative, with respect to y, thinking of x as a constant.
We find
Example: Of course, if you have a function, such as h(t) = 5t + In t, which depends on only one variable, the partial derivative is just the same as the ordinary derivative: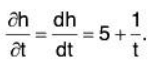
It’s not wrong to write the partial derivative here, but it could be misleading in some cases; it might make someone wonder what the other variables are.
Example: Find the partial derivatives of xy2 + 5y3.
First, calculate the partial derivative with respect to x, by thinking of y as constant: we find
Now, calculate the partial derivative with respect to y, by thinking of x as constant; we find
(Another Definition) Let f : D→ R, and (a, b) be any point of D.
The partial derivative of f w.r.t. x at the point (a, b), denoted as fx(a, b), is defined as
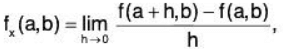
provided the limit exists.
The partial derivative of f w.r.t. y at the point (a, b), denoted as fy(a, b), is defined as

provided the limit exists.
fx(a, b), fy(a, b) are called the first order partial derivatives of f at (a, b).
Now the second order partial derivatives of f at (a, b) viz.
fxx(a,b), fyx (a,b), fxy(a,b), fyy(a,b).
Defined as
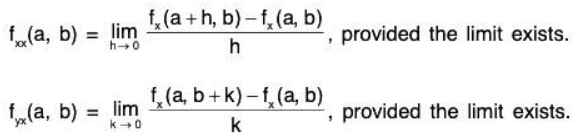
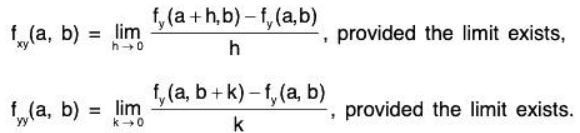
If function is continuous then fxy(a, b) = fyx(a, b).
In general, fxy(a,b) ≠ fyx(a,b)
Example 2: The volume, V, of a right circular cylinder is given by V = πr2h, where r is the radius of the base, and h is the height. Suppose that the cylinder is some sort of container for which the height can vary, such as the interior of a piston.
What is the instantaneous rate of change of the volume, with respect to the height, when the height is 0.3 meters, if the radius is held constant at 0.1 meters?
We hold r constant and find
in cubic meters per meter (or, square meters).
Thus, the instantaneous rate of change of the volume, with respect to the height, when the height is 0.3 m, and the radius is held constant at 0.1 m is
Note that this result is independent of h, so that, in the end, we don’t need to use the data that h = 0.3 meters.
Example. Suppose that we have the function
w = f(x,y,z) = x sin(yz) + y2ez + x3.
Then, we find: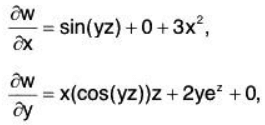
and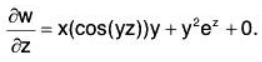
Theorem: If U is a non-empty connected open subset of Rn, and f is a function on U such that all of the partial derivatives of f exist and are 0 at each point in U, then f is constant on U.
Definition: The multi-component function
of partial derivatives of a function f = f(x1,...,xn) is called the gradient vector (function) of f. Its value at a point p is denoted either by 
Example: Consider f(x,y) = x2 - y2. Then,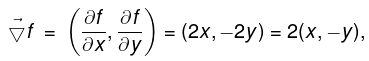
and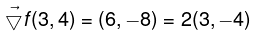
Higher-order partial derivatives:
Consider the function
f(x,y) = x2 + 5xy - 4y2.
The partial derivatives are easy to calculate: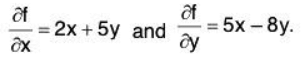
We now want to look at the second partial derivatives of f.
A second partial derivative should be a partial derivative of a partial derivative. So, there are four second partial derivatives: you can first take two different first partial derivatives, with respect to x or y and then, for each of those, you can take a partial derivative a second time with respect to x or y. We introduce new notation, and calculate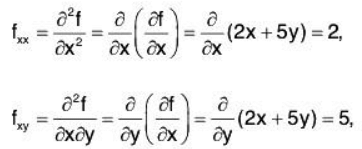
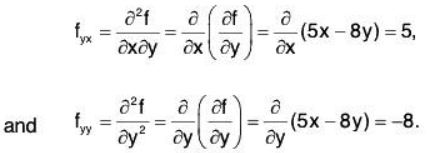
The two second partial derivatives fxy and fyx above, the ones with one partial derivative with respect to x and one with respect to y, are called mixed partial derivatives.
Note that fxy and fyx are equal in this example. While this is not always the case, it's true for “most” of the functions that we deal with. More precisely, we need the continuity condition given in the following theorem.
Theorem: Suppose that f, fx, fy, and fxy exist in an open ball around a point (x0, y0), and that fxy is continuous at (x0, y0). Then, fyx(x0, y0) exists and
fyx(x0, y0) = fxy (xo > y0)
Example. Let’s try calculating some more-complicated partial derivatives. Suppose that
z = f(x,y) = x sin(xy) + 3y4.
We want to calculate the partial derivatives ∂f/∂x and ∂f/∂y. Note that x sin(xy) is the product of two functions of x, which will require the Product Rule when differentiating with respect to x. However, when we take the partial derivative with respect to y, we should think of x sin(xy) as being a “constant" times a function of y; hence, we will not need the Product Rule when applying ∂/∂y.
We find: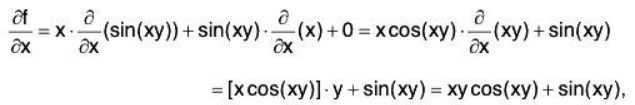
and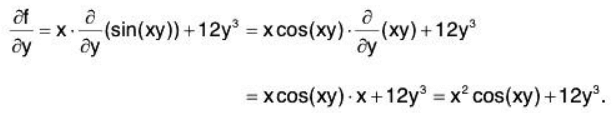
Example: Suppose that g(x,y) = xey + y2 tan-1x. Calculate the dot product.
We find
and so
Therefore,
Definition: Suppose that f(x1, x2,...,xn) is a real-valued function whose domain is a subset of Rn. Then, we define the partial derivative of f with respect to x, to be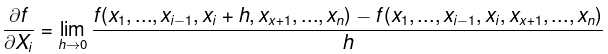
provided that this limit exists. If the Limit fails to exist, then we say that the partial derivative is undefined.
Recalling that e, denotes the i-th standard basis element and letting x = (x1,x2,...,xn), then the definition above is equivalent to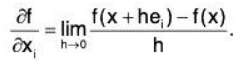
Theorem: If u is a non-empty connected open subset of Rn, and f and g are two functions on u such that all of the partial derivative of f and g exist and are equal at each point in u, then f and g differ by a constant on u, i.e., there exists a constant C such that, for all p in u, f(p) = g(p) + C.
Theorem: Suppose that f(x1, x2,...,xn) is a real-valued function such that f and all of its partial derivatives of order less than or equal to r are defined and continuous on an open subset u of Rn. Then, at each point p in u, every partial derivative of order r is independent of the order in which the partial derivatives are calculated.
Example. Suppose that
f(x,y,z) = x5y6z7 + xeyz + y2sin(3x - 5z).
Then, Theorem implies that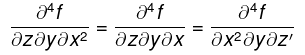
which are equal to every other 4th order partial derivative that’s with respect to x twice, and y and z once each.
They’re all equal to
840x3y5z6 + 90y cos(3x - 5x).
Example. Let
f(r, 0) = (r cos θ, r sin θ).
Then
fr = (cosθ, sinθ),
fθ = (-r sin θ, r cos θ),
frr = (0, 0)
frθ = ( - r cos θ, - r sin θ),
and
frθ = fθr = (- sinθ, cosθ).
Differentiability of Two Variables
Definition: Let f : D → R be a real-valued function defined. Then f is said to be differentiable at a point (a, b) ∈ D, if
where A and B are real numbers independent of h and k, and g is a real-valued function such that 
Equivalently, f is differentiable at (a, b), if
f(a + h, b + k) - f(a, b) = Ah + Bk + hϕ(h, k) + kψ(h, k)
where A and B are real numbers independent of h and k and ϕ(h, k), ψ(h, k) → 0 as (h, k) → ( 0,0).
Theorem: If a function f: D → R is differentiable at (a, b) ∈ D, then f has partial derivatives fx and fy at (a, b).
Proof. Since f is differentiable at the point (a, b) ∈ D, so there exist real numbers A and B, and a function g such that
(i) 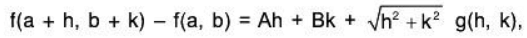 ...(1)
...(1)
(ii) A and B are independent of h and k, and
(iii) 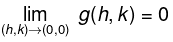
Putting k = 0 in (1), we have
f(a + h, b) - f(a,b) = Ah + |h| g(h, 0).
Dividing throughout by h, and taking limits as h → 0, we have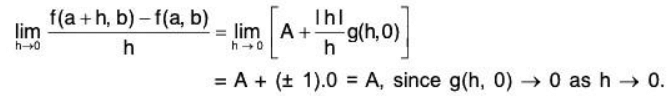
∴ fx(a, b) = A.
Putting h = 0 in (1),
we have f(a, b + k) - f(a, b) = Bk + |k| g(0, k).
Dividing throughout by k, and taking limits as k → 0, we have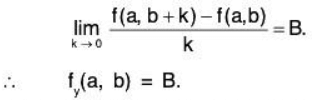
Hence fx and fy exist at the point (a, b).
Remark
- It may be noted that the constants A, B appearing in the definition of differentiability of f are given by : A = fx(a, b), B = fy(a, b).
- If either of fx, fy does not exist at (a, b), then f is not differentiable at (a, b).
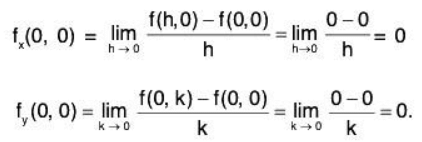
Example: Let f : R2 → R be defined by setting.
f(x, y) = xy / √(x2 + y2), when (x, y) ≠ (0, 0), f(0, 0) = 0.
fx and fy exist at (0, 0) but f is not differentiable at (0, 0). Also f is continuous at (0, 0).
Thus fx(0,0) and fy(0,0) both exist and are equal to 0.
Let, if possible, f be differentiable at (0,0). Then
f(h, k) - f(0, 0) = Ah + Bk + √(h2 + k2) g(h, k), ..... (1)
where... (2)
and A = fx(0, 0) = 0, B = fy (0, 0) = 0.
From (1), we obtain hk/√(h2 + k2) - 0 = O.h + O.k + √(h2 + k2) g(h, k),
Taking k = mh, we see thatwhich depends on m.
Thusdoes not exist, which contradicts (2).
Hence f is not differentiable at (0,0) f is continuous at (0,0).
Theorem: If f(x, y) is differentiable at a point (a, b), then it is continuous at (a, b), but converse need not be true.
i.e. Differentiability implies continuity but continuity need not imply differentiability.
Proof: Since f(x, y) is differentiable at the point (a, b), therefore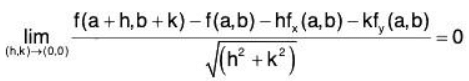
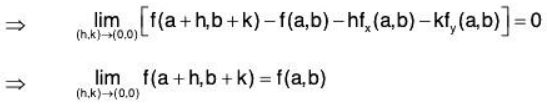
which shows that f is continuous at (a, b).
Remark: If a function f : D → R is differentiable at a point (a, b) ε D then all of its partial derivative exists but not conversely i.e. the existence of partial derivatives of the function f at a point does not imply it is differentiable.
Theorem: If a function f : D → R has continuous partial derivatives fx and fy at (a, b) ∈ D, then f is differentiable at (a, b).
Proof. Since fx and fy are continuous at (a, b), so fx and fy both exist in a nbd. N ≡ N((a, b), δ) of (a, b). Let (a + h, b + k) be any point of N. We have
f(a + h, b + k) - f(a, b) = [f(a + h, b + k) - f(a + h, b)] + [f(a + h, b) - f(a, b)] ...(1)
We define two functions G and H as follows:
G(y) = f(a + h, y) ∀ y ∈ [b, b + k],
and H(x) = f(x, b) ∀ x ∈ [a, a + h].
Since fy exists in N, so the function G satisfies both the conditions of Lagrange's mean value theorem in [b, b + k]. Thus there exists a θ1(0 < θ1 < 1) such that
G(b + k) - G(b) = kG’(b + 0,k)
or f(a + h, b + k) - f(a + h, b) = kfy(a + h, b + θ1k). ...(2)
Similarly, since H satisfies both the conditions of Lagrange’s mean value theorem in [a, a + h], there exists θ2(0 < θ2 < 1) such that
f(a + h, b) - f(a, b) = hfx(a + θ2h, b). ...(3)
Using (2) and (3) in (1), we obtain
f(a + h, b + k) - f(a, b) = hfx(a + θ2h, b) + kfy(a + h, b + θ1k)
= hfx(a, b) + kfy(a, b) + h[fx(a + θ2h, b) - fx(a, b)] + k[fy(a + h, b + θ1k) - fy(a, b)]
= hfx(a, b) + kfy(a, b) + √(h2 + k2). F(h, k), ...(4)
where F(h, k) = h[fx(a + θ2h, b) - fx(a, b)]/√(h2 + k2) + k[fy(a + h, b + θ1k) - fy(a, b)]/√(h2 + k2). ...(5)
Since fx and fy are both continuous at (a, b), so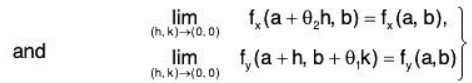 ....(6)
....(6)
From (5) and (6), we obtain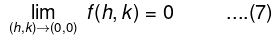
since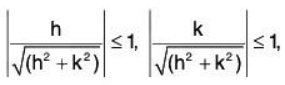
for all value of (h, k), such that h2 + k2≠ 0.
From (4) and (7), we get
f(a + h, b + k) - f(a, b) = hfx(a, b) + kfy(a, b) + √(h2 + k2) F(h, k),
where F(h, k) → 0 as (h, k) → (0, 0).
Hence f is differentiable at (a, b).
Remark: If a function f is not differentiable at (a, b), then f and f cannot be continuous at (a, b).
Theorem: If a function f(x,y) is totally differentiable the partial derivatives fx and fy both exist and are finite.
Proof. Let f(x,y) be totally differentiable at the point (a,b), then there exist two constants α and β such that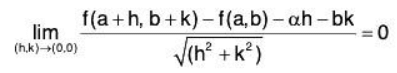
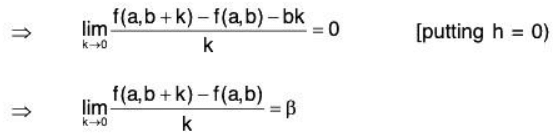
⇒ fy (a, b) = β
Similarly, fx(a,b) = α.
Accordingly by theorem a function f(x,y) can be defined at the point (a,b), if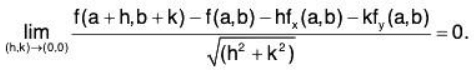
➤ Total Differential:
Theorem: If u = f (x, y) be any differentiable function, then
du = fx(x,y) dx + fy(x, y) dy.
Proof: Let u = f(x, y) be any differentiable function, then
δu = (u + δu) - u = f (x + h, y + k) - f (x, y)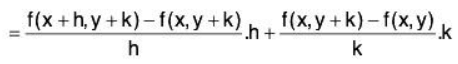
Hence h → 0 and k → 0 i.e., taking 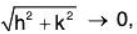
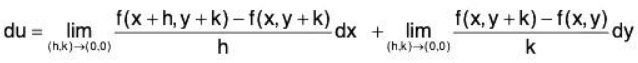
= fx(x, y) dx + fy(x, y) dy, [by mean value theorem]
Here du is the total differential of u.
➤ Sufficient Condition for Differentiability:
Theorem: If (a, b) be a point of the domain D ⊂ R2 of a real, valued function f(x, y) such that
(i) fx(a,b) exists
(ii) fy(x,y) is continuous at (a,b), then f(x,y) is differentiable at (a,b)
Proof: Let ε > 0 be given. Since fx(x,y) exists at (a, b), therefore there exists a δ1 > 0 such that Ihl < δ1, then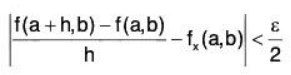
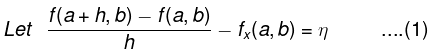
where lηl < ε/2.
Again fy(x, y) exists and continuous at (a, b), therefore by mean value theorem, f(a + h, b + k) - f(a + h, b) = k fy(a + h, b + 0k) (0 < 0 < 1) ...(2)
Now consider the following: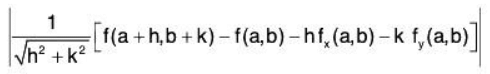
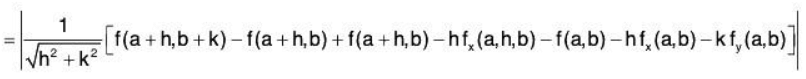
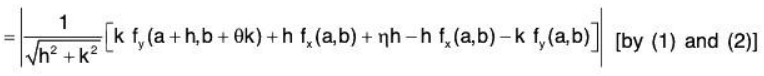
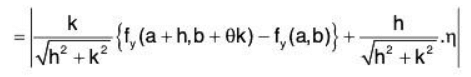
 .....(3)
.....(3)
Since fy(x, y) is continuous at (a, b), therefore for Ihl < δ2 and Ikl < δ2 there exist δ2 > 0 such that | fy(a + h, b + k) - fy(a + b) I < ε/2 .... (4)
Since h ≠ 0, k ≠ 0, then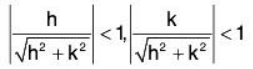 ........(5)
........(5)
Let δ = min(δ1, δ2), then Ihl < δ and Ikl < δ, With the help of (4) and (5), the in equality reduces to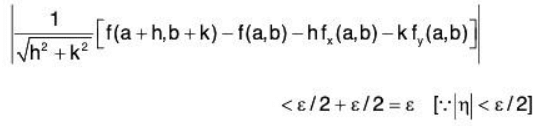
Now taking ε → 0 as h → 0, k → 0,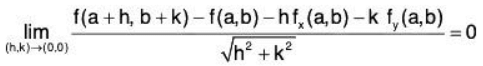
Consequently, f(x,y) is differentiable at (a,b).
➤ Some theorems of Differentiability of Real Valued Functions of Two Variables:
Theorem: If f(x,y) and g(x,y) are differentiable at (a,b) then their Sum, Difference, Product and Quotient are also differentiable at the point (a, b) i.e.,
(i) f(x, y) ± g(x, y) is differentiable and d(f ± g) = df + dg.
(ii) f(x, y) g(x, y) is differentiable and d(fg) = fdg + gdf.
(iii) f(x, y) / g(x, y) is differentiable when g(x, y) ≠ 0 and d(f/g) = (gdf - fdg) / g2
Condition for Differentiability in Polar Co-ordinates:
Let f(x, y) be differentiable at (a, b), then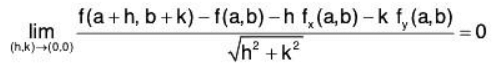
Substituting h = r cos θ and k = r sin θ and taking limit r→ 0,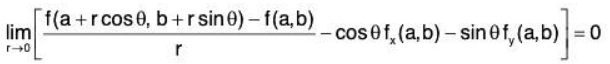
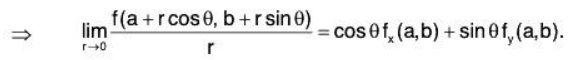
Example 1: 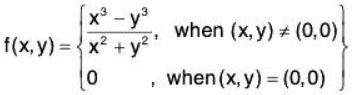
Show that the function f is not differentiable at the origin.
Both the partial derivatives exists but are not equal. Therefore, f is not differentiable at (0, 0).
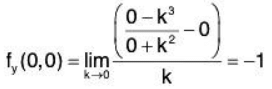
Example 2: Show that the function f(x, y) defined by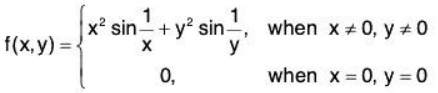 is differentiable at (0, 0).
is differentiable at (0, 0).
By definition,
Similarly, fy(0, 0) = 0
Now h = r cos θ and k = r sin θ, then[ ∵ f(0 ,1 ) = 0, fx(0,0 ) = 0 and fy(0,0) = 0]
Hence the function f(x,y) is differential at (0,0).
Example 3: Let f : R2 → R be defined by setting
f(x, y) = x2 sin (1/x) + y2 sin (1/y), when xy ≠ 0,
f(x, 0) = x2 sin (1/x), when x ≠ 0,
f(0, y) = y2 sin (1/y), when y ≠ 0,
f(0, 0) = 0.
We have
fx(x, y) = 2x sin (1/x) - cos (1/x), x ≠ 0,
fx (0, y) = 0.Again fy(x, y) = 2y sin (1/y) - sin (1/y), y ≠ 0,
fy(x, 0) = 0.
Sincedoes not exist, so by (1), fx is not continuous at (0, 0). Similarly fy is not continuous at (0, 0).
NowSimilarly fy(0, 0) = 0. Thus fx, fy both exist at (0, 0) but are not continuous at (0, 0). f is differentiable at (0, 0).
We shall verify thatwhere
We know A = fx(0, 0) = 0, B = fy(0, 0) = 0. Also f(0, 0) = 0.
From (2) and (3), we obtainHence f is differentiable at (0, 0).
Example 4: Show that the function 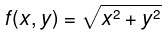 is not differentiable at (0, 0).
is not differentiable at (0, 0).
If f were differetiable then the partial derivatives
would exist. But that partial derivative is the limit.
Now notice that √h2/h is +1 if h > 0 and -1 if h < 0. Therefore, the limit as h → 0 does not exist and so the partial derivative does not exist. Hence f(x,y) is not differentiable at (0, 0).
Example 5: Show that the function is not continuous at (0, 0) (and therefore not differentiable there) even though fx(0,0) and fy(0,0) exist.
is not continuous at (0, 0) (and therefore not differentiable there) even though fx(0,0) and fy(0,0) exist.
Continuity implies that
along any curve through (0, 0). If we approach the origin along the line y = x then:
Hence, f(x,y) is not continuous at (0,0). However, the partial derivatives do exist at (0,0):
Theorem: If f(x,y), fx(x,y), and fy(x,y) are continuous for all (x, y) in the disk (x - a)2 + (y - b)2 < δ, for some δ > 0 then f(x, y) is differentiable at (a, b).
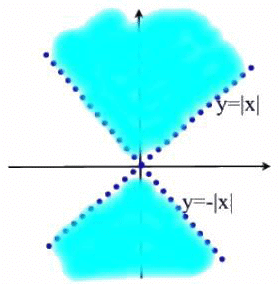
Example 6: In what region is the function 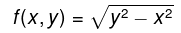 differentiable?
differentiable?
Since fx(x,y) = - x(y2- x2)-1/2 and fy(x,y) = y(y2 - x2)-1/2, according to the above theorem the function is differentiable every where in the region above y = Ixl and below y = -|x| as shown in Fig.
|
98 videos|27 docs|30 tests
|

|
Explore Courses for Mathematics exam
|

|
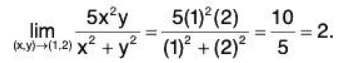
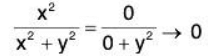
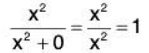
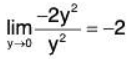
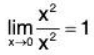
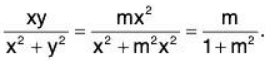


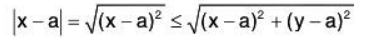
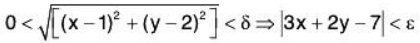
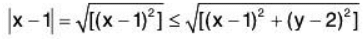

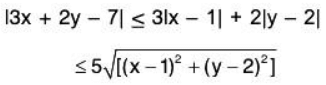


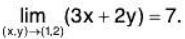
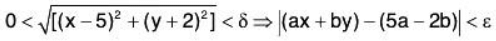
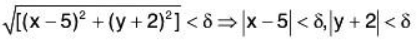
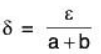
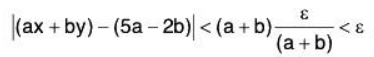
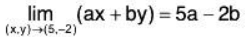

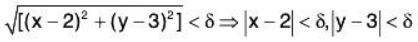
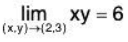
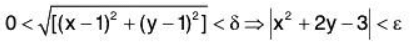
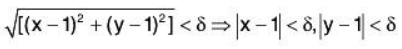
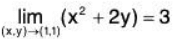
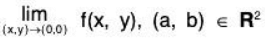 exists, then this limit is independent of path of approach along which we approach the point (a, b).
exists, then this limit is independent of path of approach along which we approach the point (a, b).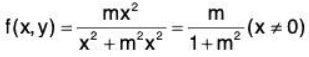
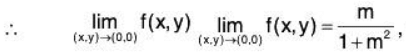 which depends on m., i.e., the limit of the function depends on the path of approach.
which depends on m., i.e., the limit of the function depends on the path of approach.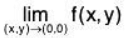 does not exist.
does not exist.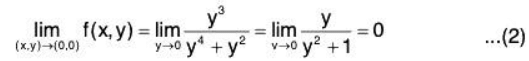
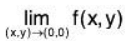 does not exist.
does not exist.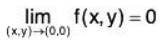 ....(2)
....(2)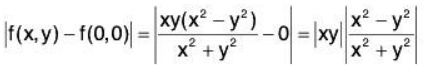
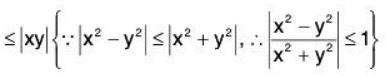
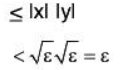
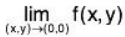 exists and equal to 0.
exists and equal to 0.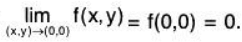
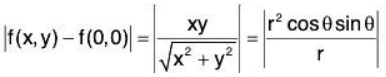
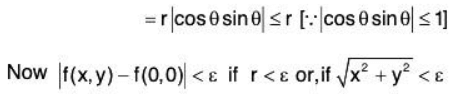
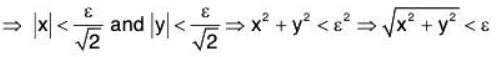
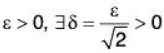 such that
such that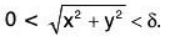
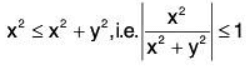 we have
we have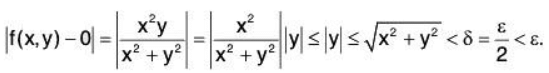
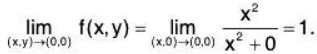
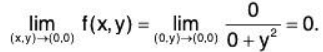
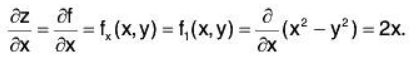
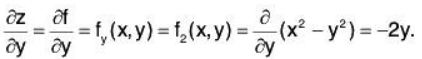
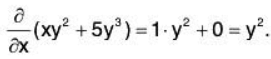
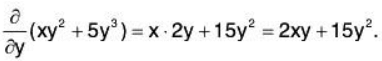
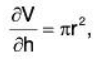
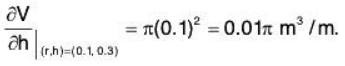
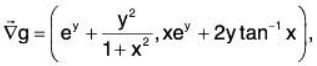
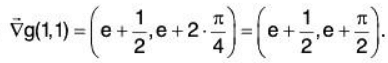
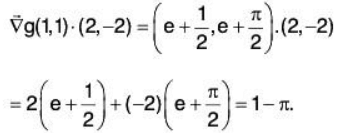
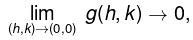 ... (2)
... (2)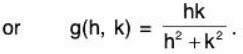
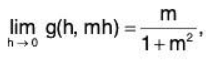 which depends on m.
which depends on m.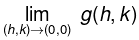 does not exist, which contradicts (2).
does not exist, which contradicts (2).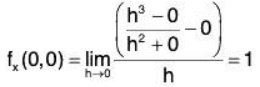
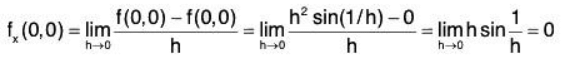
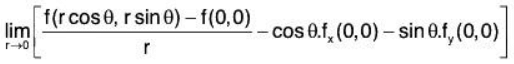
 [ ∵ f(0 ,1 ) = 0, fx(0,0 ) = 0 and fy(0,0) = 0]
[ ∵ f(0 ,1 ) = 0, fx(0,0 ) = 0 and fy(0,0) = 0]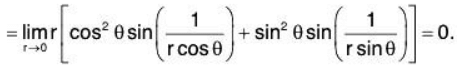
 does not exist, so by (1), fx is not continuous at (0, 0). Similarly fy is not continuous at (0, 0).
does not exist, so by (1), fx is not continuous at (0, 0). Similarly fy is not continuous at (0, 0).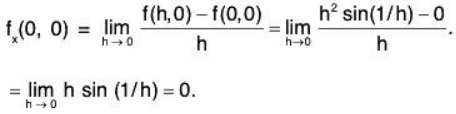
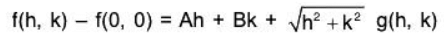 where
where 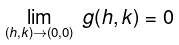 We know A = fx(0, 0) = 0, B = fy(0, 0) = 0. Also f(0, 0) = 0.
We know A = fx(0, 0) = 0, B = fy(0, 0) = 0. Also f(0, 0) = 0.
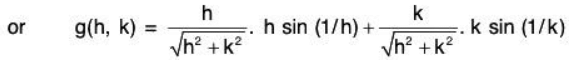

 Hence f is differentiable at (0, 0).
Hence f is differentiable at (0, 0). would exist. But that partial derivative is the limit.
would exist. But that partial derivative is the limit.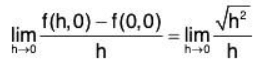 Now notice that √h2/h is +1 if h > 0 and -1 if h < 0. Therefore, the limit as h → 0 does not exist and so the partial derivative does not exist. Hence f(x,y) is not differentiable at (0, 0).
Now notice that √h2/h is +1 if h > 0 and -1 if h < 0. Therefore, the limit as h → 0 does not exist and so the partial derivative does not exist. Hence f(x,y) is not differentiable at (0, 0).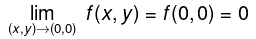 along any curve through (0, 0). If we approach the origin along the line y = x then:
along any curve through (0, 0). If we approach the origin along the line y = x then: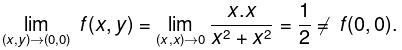 Hence, f(x,y) is not continuous at (0,0). However, the partial derivatives do exist at (0,0):
Hence, f(x,y) is not continuous at (0,0). However, the partial derivatives do exist at (0,0):