Ideal Gas & Kinetic Theory of Gases | Physical Chemistry PDF Download
| Table of contents |

|
| What is Gas? |

|
| Physical Characteristics of Gases |

|
| Parameters Associated with Gases |

|
| Ideal Gas |

|
| Kinetic Gas Theory |

|
What is Gas?
Gas is the state of matter in which the particles are far apart, fast-moving and not organized in any particular way.
- Gas is one of the four fundamental states of matter (the others being solid, liquid, and plasma).
- A pure gas may be made up of individual atoms (e.g. a noble gas like neon), elemental molecules made from one type of atom (e.g. oxygen), or compound molecules made from a variety of atoms (e.g. carbon dioxide).
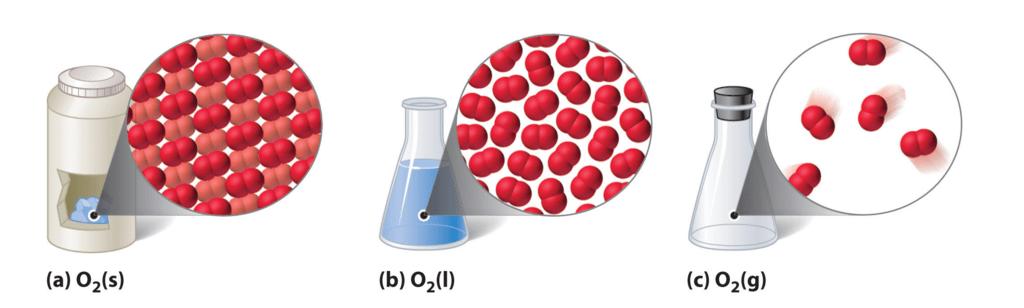
- A gas mixture would contain a variety of pure gases, much like the air.
- The interaction of gas particles in the presence of electric and gravitational fields is considered negligible as indicated by the constant velocity vectors in the image.
- The gaseous state of matter is found between the liquid and plasma states, the latter of which provides the upper-temperature boundary for gases.
- It is important to note that substances that exist in the gaseous state do not have any definite volume or any definite shape.
- They tend to occupy the entire volume of the container they are placed in. Furthermore, gases are highly compressible and are known to exert some finite pressure on the walls of their containers.
Physical Characteristics of Gases
- Gases have a lower density and are highly compressible as compared to solids and liquids.
- They exert an equal amount of pressure in all directions.
- The space between gas particles is a lot, and they have high kinetic energy.
- The intermolecular forces between these gas particles are negligible.
- These particles move at high speeds in all directions and hit each other, thus causing the gas to spread throughout the container they are kept in, evenly. This also causes them to exert pressure on the walls of the container.
- So, gases take the volume and shape of the container.
Parameters Associated with Gases
Because most gases are difficult to observe directly, they are described through the use of four physical properties or macroscopic characteristics: pressure, volume, number of particles (chemists group them by moles) and temperature.
- These four characteristics were repeatedly observed by scientists such as Robert Boyle, Jacques Charles, John Dalton, Joseph Gay-Lussac, and Amedeo Avogadro for a variety of gases in various settings.
- Their detailed studies ultimately led to a mathematical relationship among these properties expressed by the ideal gas law
Pressure
Pressure is the sum of all the normal components of force exerted by the particles impacting the walls of the container divided by the surface area of the wall.
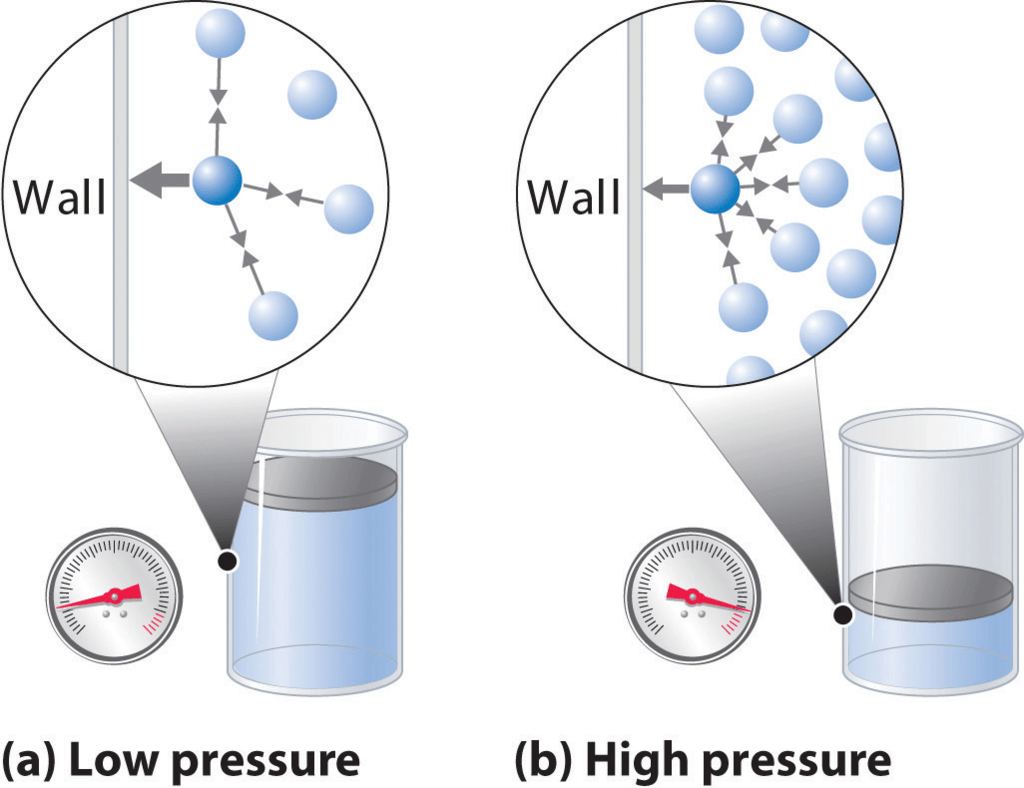 The Effect of Intermolecular Attractive Forces on the Pressure a Gas Exerted on the Container Walls
The Effect of Intermolecular Attractive Forces on the Pressure a Gas Exerted on the Container Walls
- The symbol used to represent pressure in equations is "p" or "P" with SI units of pascals.
- When describing a container of gas, the term pressure (or absolute pressure) refers to the average force per unit area that the gas exerts on the surface of the container.
- Within this volume, it is sometimes easier to visualize the gas particles moving in straight lines until they collide with the container.
- The force imparted by a gas particle into the container during this collision is the change in momentum of the particle.
- During the collision, only the normal component of velocity changes. A particle traveling parallel to the wall does not change its momentum.
- Therefore, the average force on a surface must be the average change in linear momentum from all of these gas particle collisions.
- Hence, Pressure is the sum of all the normal components of force exerted by the particles impacting the walls of the container divided by the surface area of the wall.
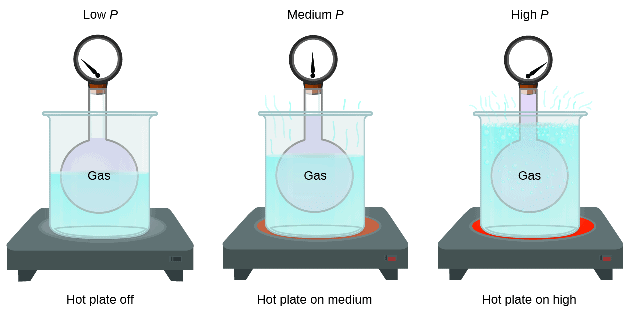 Pressure and Temperature Relation
Pressure and Temperature Relation
Temperature
The symbol used to represent the temperature in equations is T with SI units of kelvins.
The speed of a gas particle is proportional to its absolute temperature.
- The volume of the balloon shrinks when the trapped gas particles slow down with the addition of extremely cold nitrogen.
- The temperature of any physical system is related to the motions of the particles (molecules and atoms) which make up the [gas] system.
- In statistical mechanics, the temperature is the measure of the average kinetic energy stored in a particle.
- The methods of storing this energy are dictated by the degrees of freedom of the particle itself (energy modes). Kinetic energy added (endothermic process) to gas particles by way of collisions produces linear, rotational, and vibrational motion.
- In contrast, a molecule in a solid can only increase its vibrational modes with the addition of heat as the lattice crystal structure prevents both linear and rotational motions.
- These heated gas molecules have a greater speed range which constantly varies due to constant collisions with other particles.
- The speed range can be described by the Maxwell–Boltzmann distribution. Use of this distribution implies ideal gases near thermodynamic equilibrium for the system of particles being considered.
Specific Volume
The symbol used to represent specific volume in equations is "v" with SI units of cubic meters per kilogram.
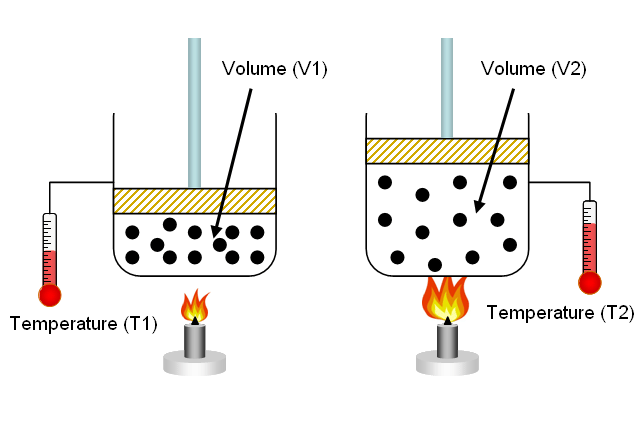 Temperature- Volume Relation
Temperature- Volume Relation
- When performing a thermodynamic analysis, it is typical to speak of intensive and extensive properties.
- Properties that depend on the amount of gas (either by mass or volume) are called extensive properties, while properties that do not depend on the amount of gas are called intensive properties.
- Specific volume is an example of an intensive property because it is the ratio of the volume occupied by a unit of mass of a gas that is identical throughout a system at equilibrium.
- 1000 atoms a gas occupy the same space as any other 1000 atoms for any given temperature and pressure.
- This concept is easier to visualize for solids such as iron which is incompressible compared to gases. Since a gas fills any container in which it is placed, volume is an extensive property.
Density
The symbol used to represent density in equations is ρ (rho) with SI units of kilograms per cubic meter. This term is the reciprocal of specific volume.
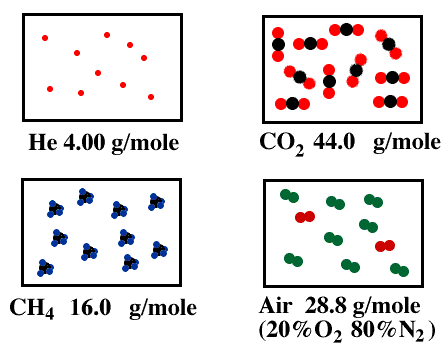 Density of Various Gases
Density of Various Gases
- Since gas molecules can move freely within a container, their mass is normally characterized by density.
- Density is the amount of mass per unit volume of a substance or the inverse of a specific volume. For gases, the density can vary over a wide range because the particles are free to move closer together when constrained by pressure or volume.
- This variation of density is referred to as compressibility. As pressure and temperature, density is a state variable of a gas, and the change in density during any process is governed by the laws of thermodynamics.
- For a static gas, the density is the same throughout the entire container. Density is, therefore, a scalar quantity.
- It can be shown by the kinetic theory that the density is inversely proportional to the size of the container in which a fixed mass of gas is confined. In this case of a fixed mass, density decreases as the volume increases.
Ideal Gas
An ideal gas is defined as a gas that obeys gas laws at all condition of pressure and temperature.
- Ideal gases have velocity and mass.
- They do not have volume.
- When compared to the total volume of the gas the volume occupied by the gas is negligible.
- It does not condense and does not have triple point.
- While a real gas has negligible intermolecular forces of attraction, an ideal gas has zero inter-molecular forces of attraction because the molecules of an ideal gas move so fast, and they are so far away from each other that they do not interact at all.
- There is no ideal gas that exists naturally. However, gases behave most ideally at high temperatures and low-pressure conditions. The behavior of gases is governed by certain laws.
Microscopic View of a Gas: Elastic collision in Ideal Gas
- If one could observe a gas under a powerful microscope, one would see a collection of particles (molecules, atoms, ions, electrons, etc.) without any definite shape or volume that are in more or less random motion.
- These neutral gas particles only change direction when they collide with another particle or with the sides of the container.
- In an ideal gas, these collisions are perfectly elastic. This particle or microscopic view of a gas is described by the Kinetic-molecular theory.
Postulates of an Ideal Gas:
The essential postulates are :
- A gas consists of a large number of very small spherical tiny particles, which may be identified with the molecules.
- The molecules of a given gas are completely identical in size, shape, and mass.
- The volume occupied by the molecules is negligible in comparison to the total volume of the gas.
- The molecules are in rapid motion which is completely random. During their motion, they collide with one another and with the sides of the vessel. The pressure of the gas is due to the collisions of molecules with the sides of the vessel.
- The molecules are perfectly elastic, i.e. there occurs no loss of energy when they collide with one another and with the sides of the vessel.
- The laws of classical mechanics, in particular, Newton’s second law of motion, are applicable to the molecules in motion.
- There is no force of attraction or repulsion among the molecules, i.e. they are moving independently of one another.
- At any instant, a given molecule can have energy ranging from a small value to a very large value, but the average kinetic energy remains constant for a given temperature. i.e. the average kinetic energy is proportional to the absolute temperature of the gas.
Kinetic Gas Theory
Kinetic theory provides insight into the macroscopic properties of gases by considering their molecular composition and motion.
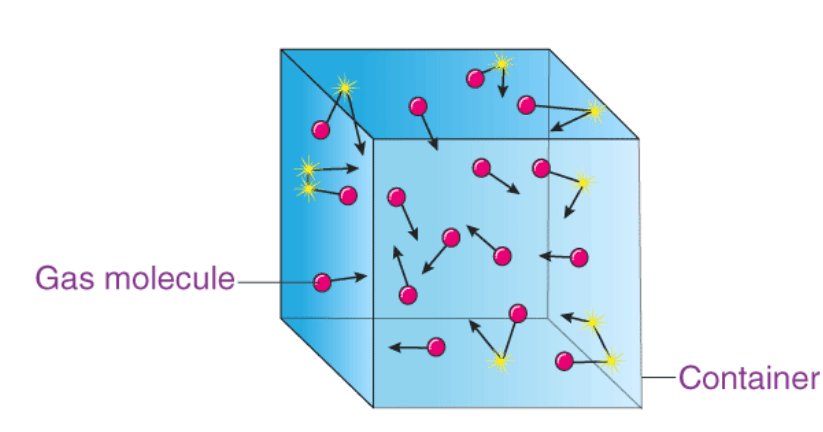
- Starting with the definitions of momentum and kinetic energy, one can use the conservation of momentum and geometric relationships of a cube to relate macroscopic system properties of temperature and pressure to the microscopic property of kinetic energy per molecule.
- The theory provides averaged values for these two properties.
- The theory also explains how the gas system responds to change. For example, as a gas is heated from absolute zero, when it is (in theory) perfectly still, its internal energy (temperature) is increased.
- As a gas is heated, the particles speed up and its temperature rises.
- This results in greater numbers of collisions with the container per unit time due to the higher particle speeds associated with elevated temperatures.
- The pressure increases in proportion to the number of collisions per unit time.
Derivation of the Kinetic Gas Equation
Imagine a cube of edge-length l, containing N molecule, each having a mass of m.
The velocity u1 of any molecule may be resolved into three-component velocities designated as ux, uy and uz.
The component velocities are related by the expression
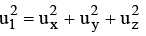 …………….(1)
…………….(1)
Considering the x-component motion of the molecule, we will have
Momentum of molecule before collision with the side ABCD = mux.
Momentum of the molecule after collision with the side ABCD = –mux.
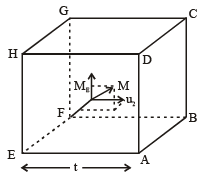
Change of momentum of the molecule in a single collision with the side ABCD = |2mux|.
The total change of momentum per unit time due to such impacts is 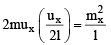
The area of the wall is l2. Hence the pressure exerted due to the collision of the x-component velocity of a single molecule with the side ABCD is
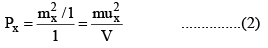
Where V is the volume of the vessel.
Since each molecule will exert similar pressure, the total pressure exerted on the wall ABCD will be
 ...............(3)
...............(3)
Defining the mean square speed as
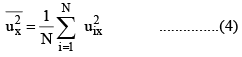
we can write

Since the directions x, y and z are equivalent will also have

But from eq. (1) we have
 ...(7)
...(7)
From eq. (6) and (7) we have
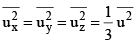 ...(8)
...(8)
Substituting this in eq. (5) we get
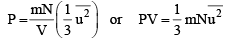 ....(9)
....(9)
Brownian motion
Brownian motion is the mathematical model used to describe the random movement of particles suspended in a fluid. The gas particle animation, using pink and green particles, illustrates how this behavior results in the spreading out of gases (entropy).
 Brownian motion
Brownian motion
Since it is at the limit of (or beyond) current technology to observe individual gas particles (atoms or molecules), only theoretical calculations give suggestions about how they move, but their motion is different from Brownian motion because Brownian motion involves a smooth drag due to the frictional force of many gas molecules, punctuated by violent collisions of an individual (or several) gas molecule(s) with the particle.
Intermolecular forces
Momentary attractions (or repulsions) between particles have an effect on gas dynamics. In physical chemistry, the name given to these intermolecular forces is vander Waals force.
- These forces play a key role in determining physical properties of a gas such as viscosity and flow rate. Ignoring these forces in certain conditions allows a real gas to be treated like an ideal gas.
- This assumption allows the use of ideal gas laws which greatly simplifies calculations.
- Proper use of these gas relationships requires the kinetic-molecular theory (KMT). When gas particles experience intermolecular forces they gradually influence one another as the spacing between them is reduced (the hydrogen bond model illustrates one example).
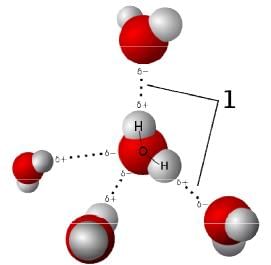 Inter-molecule forces between H2O molecule
Inter-molecule forces between H2O molecule - In the absence of any charge, at some point when the spacing between gas particles is greatly reduced they can no longer avoid collisions between themselves at normal gas temperatures.
- Another case for increased collisions among gas particles would include a fixed volume of gas, which upon heating would contain very fast particles.
- This means that these ideal equations provide reasonable results except for extremely high pressure (compressible) or high temperature (ionized) conditions.
- All of these excepted conditions allow energy transfer to take place within the gas system. The absence of these internal transfers is what is referred to as ideal conditions in which the energy exchange occurs only at the boundaries of the system. Real gases experience some of these collisions and intermolecular forces.
- When these collisions are statistically negligible (incompressible), results from these ideal equations are still meaningful. If the gas particles are compressed into close proximity they behave more like a liquid.
|
90 videos|144 docs|67 tests
|
FAQs on Ideal Gas & Kinetic Theory of Gases - Physical Chemistry
| 1. What is an ideal gas? |  |
| 2. What are the physical characteristics of gases? |  |
| 3. What are some parameters associated with gases? |  |
| 4. What is the kinetic theory of gases? |  |
| 5. How does the ideal gas law relate to the kinetic theory of gases? |  |

















