Maxwell Boltzmann’s Distribution & Equipartition of Energy | Physical Chemistry PDF Download
13. Distribution of Molecular Velocities (Maxwell’s and Maxwell Boltzmann’s Distribution Law of Molecular Velocities)
Due to collisions between molecules, velocity as well as direction of the movement, also changes. Thus their kinetic energies as well as, velocities are redistributed. Hence, the molecules, move with different velocities and their kinetic energies are also different. Boltzmann, gave the following expression, for the distribution of energy between molecules.
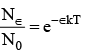 ...(1)
...(1)
Here, N0 is the total number of molecules and N∈ is the number of molecules having energy, more than a reference point ∈, k is boltzmann constant and T is absolute temperature.
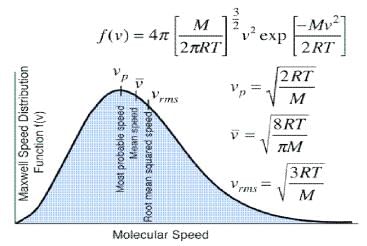
In 1860, J.C maxwell gave a law, by using the theory of probability, which is known as Law of Distribution of molecular velocities. According to this law, velocities of the molecules are distributed from zero to a great range. By using Boltzmann’s equation and probability theory. Maxwell derived a simple expression, which show that the actual distribution depends on temperature and molecular weight of the gas. The mathematical expression for the Maxwell’s distribution law is :
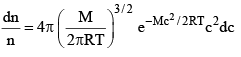 ...(2)
...(2)
velocities are between c and (c + dc). (Where dc, represents a very small difference). M, molecular weight R gas constant, T absolute temperature and e is base of natural logarithm equation (2) can also be written as
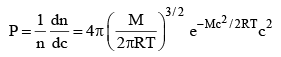 ...(3)
...(3)
where P = Probability of the molecule, whose velocity is between c and (c + dc)
Equation (3) is known as Maxwell’s Distribution Law of Maxwell Boltzmann Distribution law of molecular velocities
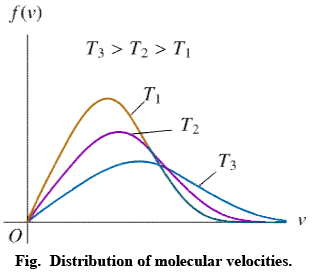
Distribution of molecular velocities is shown by (figure), where, fraction of molecules,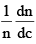 i. e. probability (P) is plotted against co-ordinate axis and velocities of the molecule c, on the abscissa, three different curves I, II and III are obtained at three different temperatures T1, T2 and T3 respectively, where (T3 > T2 > T1). This type of curve at constant temperature is known as distribution curve. Following observation can be made from the curve in:
i. e. probability (P) is plotted against co-ordinate axis and velocities of the molecule c, on the abscissa, three different curves I, II and III are obtained at three different temperatures T1, T2 and T3 respectively, where (T3 > T2 > T1). This type of curve at constant temperature is known as distribution curve. Following observation can be made from the curve in:
(i) The number of molecules having very low and very high velocities is very low.
(ii) For every curve probability or fraction of those molecules whose velocity is more than zero increases, with increasing value of velocity c, probability increases and reaches a maxima and then readily decreases. As velocity c increases, probability decreases, because by increase in the value of c2 the value of exponential term (equation 3) decreases. Thus fraction of molecules having very low velocities, is very low.
(iii) Curve is asymmetrical and has clear maxima. At every temperature most of the molecules, have the velocity of the maxima. This value of velocity is known as most probable velocity and is denoted by α.
(iv) Curve is asymmetrical near maxima, hence most probable velocity does not coincide with average velocity.
(v) Effect of temperature on distribution of Velocities – T3 > T2 > T1 respectively, which show that by increase in temperature fraction of molecules having velocity higher than a definite value.
Value of most probable velocity increases with increase in temperature (figure). By increase in temperature, the curve shifts towards right side. Height of the maxima decreases and width of the curve increases, which shows that at high temperatures, number of fraction of molecules having velocity higher than an average velocity increases, but fraction of molecules having most probable velocity decreases.
It is evident from figure that the fraction of molecules, having velocity more than a reference point is low at temperature T1.
(vi) Distribution of velocity also depends on molecular weights. Eq. (3).
For example, at constant temp, distribution of velocities in O2 (mol. wt. 32), is lower than in N2 (mol. wt. 28) in above figure.
14. Average Kinetic Energy
The average kinet ic energy is defined as
is defined as
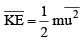
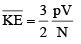
For 1 mole of an ideal gas
PV = RT and N = NA
With these, the above equation becomes
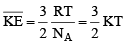
where  and is known as the Boltzmann constant. Its value is given by
and is known as the Boltzmann constant. Its value is given by

· Total kinetic energy of a single molecule 
k = Boltzman constant = 1.3806 × 10–16 erg deg–1.
· Total kinetic energy for one mole of a gas = 3/2 RT.
15. Derivation of some expression from the Maxwell Distribution
1. Average Speed: The average value of speed is given by the relation
where dNu is the number of molecules having speed u. The summation of different speeds is replaced by integration since all types of speed raning from zero to infinity are involved.
2. Root Mean Square speed : The mean square speed is given by
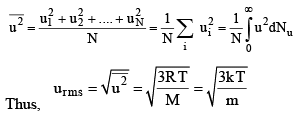
Thus, rms speed is directly proportional to the square root of temperature and inversely proportional to the square root of molar mass. Hence, at a given temperature lighter molecules (say H2, He) move faster than the heavier molecules (say O2, N2). There is no effect of change of pressure or volume on the rms speed since, at a given temperature, PV = constant.
3. Most Probable Speed ump
It is the speed possessed by maximum fraction of molecules at particular temperature.

R = Universal gas constant
M = Molecular mass
m = Mass of molecule
16. Mean free path: A very important quantity in kinetic theory of gases is the mean free path. ₹, defined as the mean distance travelled by a gas molecule between two successive collisions. Evidently,

k = Boltzman constant ; σ = collision diameter .
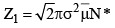 [collisions made by one molecule]
[collisions made by one molecule]

From eq. 4, we see that λ ∝ 1/P, i.e. the mean free path of a gas molecule is inversely proportional to pressure. This fact is of tremendous importance in vacuum system. It should be borne in mind that at a atm pressure, λ is very small compared with the macroscopic dimensions (such as 1 cm) which implies that the molecules collide with one another far more frequently than they collide with the walls of the container and that a molecule moves a distance of several molecular diameters before colliding with another molecule.
17. Law Of Equipartition of Energy
If the energy of a molecule can be written in the form of a sum of terms, each of which is proportional to the square of a velocity component (or to the square of a position coordinate), then each of these square terms contributes (1/2) kT to the average energy.
A polyatomic molecule besides having translational motion, also has rotational and vibrational motions.
1. Translational Motion
The translational energy of a gas molecule is
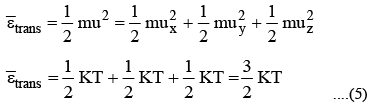
2. Rotational Motion
Average rotational energy of a linear molecule 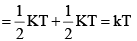
Average rotational energy of a non-linear molecule 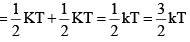
3. Vibrational Motion: εvib = kinetic energy + potential energy
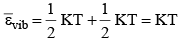
Average Kinetic Energy: The average kinetic energy  is defined as For linear molecule
is defined as For linear molecule
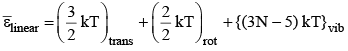
For nonlinear molecule
17. Molecular Interactions in Real Gases
Real gases show deviations from the perfect gas law because molecules interact with each other. Repulsive forces between molecules assists expansion and attractive forces assist compression.
Repulsive forces are significant only when molecules are almost in contact: they are short-range interactions, even on a scale measured in molecular diameters. Because they are short-range interactions, repulsion can be expected to be important only when the average separation of the molecules is small.
The variation of the potential energy of two molecules on their separation. High positive potential energy (at very small separations) indicates that the interactions between them are strongly repulsive at these distances. At intermediate separations, where the potential energy is negative, the attractive interactions dominate. At large separations (on the right) the potential energy is zero and there is no interaction between the molecules
18. Deviation from Ideality and Compression factor
The compression factor, Z of a gas is the ratio of its molar volume, Vm, to the molar volume of a perfect gas, at the same pressure and temperature :
Because the molar volume of a perfect gas is equal to RT/P, an equivalent expression is
pVm = RTZ
19. Causes of Deviations from Ideal Behaviour
The ideal gas law can be derived from the kinetic theory of gases which is based on the following two important assumptions :
(i) The volume occupied by the molecules is negligible in comparison to the total volume of the gas.
(ii) The molecules exert no forces of attraction upon one another.
It is because neither of these assumptions can be regarded as applicable to real gases that the latter show departure from the ideal behaviour.
20. Evidence for Molecular Volume
The molecules of a gas, however, do occupy a certain volume as can be seen from the fact that gases can be liquefied and solidified at low temperatures and high pressures. On decreasing the temperature of a gas, the thermal energy of molecules is decreased and the effect of applying high pressure is to bring the molecules closer to one another, thereby increasing the forces of attraction among them. Both these factors favour liquification and solidification.
21. Correction for Volume
Vi in the ideal gas equation represents an ideal volume where the molecules can move freely. In real gases, a part of the total volume is, however, occupied by the molecules of the gas. Hence, the free volume Vi is the total volume V minus the volume occupied by the molecules. If b represents the effective volume occupied by the molecules of 1 mole of a gas, then for the amount on of the gas Vi is given by
Vi = V – nb ...(1)
where b is called the excluded volume or co-volume. The numerical value of b is four times the actual volume occupied by the gas molecules. This can be shown as follows :
If we consider only bimolecular collisions, then the volume occupied by the sphere of radius 2r represents the excluded volume per pair of molecules as shown in figure.
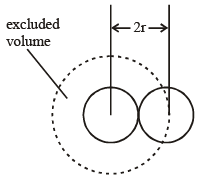
Thus, excluded volume per pair of molecules 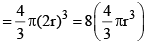
Excluded volume per molecule 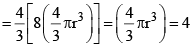 (volume occupied by a molecule)
(volume occupied by a molecule)
Since b represents excluded volume per mole of the gas, it is obvious that
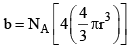
|
84 videos|142 docs|67 tests
|
FAQs on Maxwell Boltzmann’s Distribution & Equipartition of Energy - Physical Chemistry
| 1. What is Maxwell Boltzmann's distribution and how does it relate to the equipartition of energy? |  |
| 2. How does temperature affect the Maxwell Boltzmann distribution and the equipartition of energy? |  |
| 3. Can the Maxwell Boltzmann distribution be applied to all gases and particles? |  |
| 4. How does the shape of the Maxwell Boltzmann distribution change with different temperatures? |  |
| 5. What are the practical applications of the Maxwell Boltzmann distribution and the equipartition of energy? |  |






















