Generalized Coordinates - Classical Mechanics, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Generalized coordinates
Consider again the motion of a simple pendulum. Since it is one dimensional, use arc length as a coordinate. Since radius is fixed, use the angular displacement, θ, as a generalized coordinate. The equation of motion involves  it should, although the coordinate is dimensionless.
it should, although the coordinate is dimensionless.
|
Problem 5: Simple pendulum Choose θ as the generalized coordinate for a simple pendulum. |
Many particles
Following the motion of N particles requires keeping track of N vectors, x1 , x2 , · · · , xN . The configuration space has 3N dimensions; the phase space has 6N dimensions. We say that there are 3N degrees of freedom. Phase space volume has engineering dimension of (energy × time)3N .
The equations of motion are
If these are subject to some non-holonomic constraints, then there is no reduction in the number of degrees of freedom. If there are M scalar equations expressing holonomic constraints, then the number of degrees of freedom reduces to D = 3N − M . There is a consequent change in the dimension of phase space and the engineering dimension of phase space volume.
Generalized coordinates
If there are M constraints of the form fα (x1 , x2 , · · · , xN) = 0 with 1 ≤ α ≤ M , then all the coordinates of the N particles are given in terms of generalized coordinates qi where 1 ≤ i ≤ D = 3N − M .
In other words, one has N vector-valued functions xj = xj (q1 , q2 , · · · qD, t). If the generalized coordinates are to provide a complete description of the dynamics then knowledge of all the qk should be equivalent to specifying all the xj. A counting of the number of scalar equations shows that this is possible.
Clearly, the velocities are
As a result one has the important identity
Generalized forces
The equations of motion are equivalent to the principle that if one makes an instantaneous virtual displacement of a mechanical system, then the work done by the forces goes into a change of the total kinetic energy. In other words
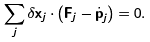
Now one can use the generalized coordinates to rewrite the work done by the forces
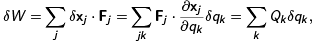
where one has defined the generalized forces

The change in kinetic energy
One can write

Equation of motion
Since the virtual displacements of the generalized coordinates are all independent, one can set each coefficient independently to zero. Then we have

If the particles move in a field of conservative forces then
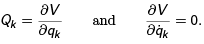
Then the equations of motion can be written in terms of the Lagrangian function L = T − V ,
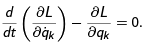
The Euler-Lagrange equations of motion
The generalized momenta are defined as

One recovers the usual definition for systems where the velocities appear only in the kinetic part of the energy. Similarly, if one considers the kinds of systems where the coordinates only appear in the potential, then
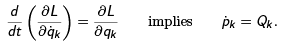
The Euler-Lagrange equations reduce to the usual form of Newton’s equations of motion in these cases. Interesting generalizations arise in other cases.
Particle in an electromagnetic field
The Lorentz force on a particle in an electromagnetic field is
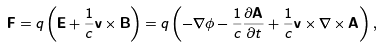
where q = charge, c = speed of light, v the velocity, E and B the electric and magnetic fields, and φ and A the scalar and vector potentials.
The Lagrangian formalism continues to be useful if one can write down a velocity dependent potential 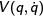 such that
such that
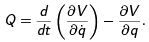
Now using the identity
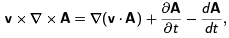
one finds that V = q(φ − v · A/c) gives the Lorentz force.
Dissipation
The problem of dissipative forces lies a little away from the developments made till now. However, models of frictional forces show that they are proportional to the velocity. Hence, for the dissipative forces on a body one may write the relation
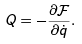
This introduces the Rayleigh term, 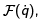 which is usually chosen to be quadratic in
which is usually chosen to be quadratic in The equations of motion are then written as
The equations of motion are then written as
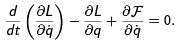
In order to describe the motion of a body in a dissipative environment both the Lagrangian L and the Rayleigh term F need to be specified.
Keywords and References
|
Keywords engineering dimensions, conservative forces, configuration space, degrees of freedom, virtual displacement, generalized coordinates, generalized forces, generalized momenta, Lagrangian function, Lorentz force, Rayleigh term |
|
556 videos|198 docs
|
FAQs on Generalized Coordinates - Classical Mechanics, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What are generalized coordinates in classical mechanics? |  |
| 2. How are generalized coordinates related to degrees of freedom in classical mechanics? |  |
| 3. Can we use any coordinate system as generalized coordinates? |  |
| 4. How do generalized coordinates simplify the equations of motion in classical mechanics? |  |
| 5. Are there any limitations or constraints on the choice of generalized coordinates? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|


















