Geometric Progression (G.P) | Mathematics (Maths) Class 11 - Commerce PDF Download
C. Geometric Progression (GP)
GP is a sequence of numbers whose first term is non zero & each of the succeeding terms is equal to the proceeding terms multiplied by a constant . Thus in a GP the ratio of successive terms is constant. This constant factor is called the COMMON RATIO of the series & is obtained by dividing any term by that which immediately proceeds it . Therefore a, ar, ar2, ar3, ar4, ...... is a GP with a as the first term & r as common ratio .
(i) nth term = a rn-1
(ii) Sum of the Ist n terms i.e.
(iii) Sum of an infinite GP when |r| < 1 when n → ∞ rn → 0 if |r| < 1 therefore, S∞ = .
(iv) If each term of a GP be multiplied or divided by the same non-zero quantity, the resulting sequence is also a GP .
(v) Any 3 consecutive terms of a GP can be taken as a/r, a, ar ; any 4 consecutive terms of a GP can be taken as a/r3, a/r, ar, ar3 & so on.
(vi) If a, b, c are in GP ⇒ b² = ac.
Ex. 9 If the first term of G.P. is 7, its nth term is 448 and sum of first n terms is 889, then find the fifth term of G.P.
Sol. Given a = 7 the first term tn = arn - 1 = 7(r)n - 1 = 44 ⇒ 7rn = 448 r
Also Sn =
⇒ 889 =
⇒ r = 2. Hence T5 = ar4 = 7(2)4 = 112
Ex.10 If the third and fourth terms of an arithmetic sequence are increased by 3 and 8 respectively, then the first four terms form a geometric sequence. Find
(i) the sum of the first four terms of A.P.
(ii) second term of the G.P.
Sol. a, (a + d), (a + 2d), (a + 3d) in A.P.
a, a + d, (a + 2d + 3), (a + 3d + 8) are in G.P.
hence a + d = ar
also r = =
=
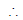
=
⇒ d2 + 6d + 9 = d2 + 5d ⇒ d = - 9
∴ =
⇒ a2 - 18a + 81 = a2 - 15a ⇒ 3a = 81 ⇒ a = 27
hence A.P. is 27, 18, 9, 0,
G.P. is 27, 18, 12, 8
(i) sum of the first four terms of A.P. = 54
(ii) 2nd term of G.P. = 18
Ex.11 Three positive numbers form a G.P. If the second term is increased by 8, the resulting sequence is an A.P. In turn, if we increase the last term of this A.P. by 64, we get a G.P. Find the three numbers.
Sol. Let the numbers be a, a r, a r2 where r > 0
Hence a, (a r + 8), a r2 in A.P. - (1)
Also a, (a r + 8), a r2 + 64 in G.P. - (2)
⇒ (a r + 8)2 = a (a r2 + 64) a = 4/4-r - (3)
Also(1) ⇒ 2 (a r + 8) = (a + a r2) ⇒ (1 - r)2 = 16/a - (4)
From (3) and (4) r = 3 or - 5 (rejected) .
Hence a = 4 numbers are : 4, 12, 36
Ex.12 The sum of the first five terms of a geometric series is 189, the sum of the first six terms is 381, and the sum of the first seven terms is 765. What is the common ratio in this series.
Sol.
S5 = 189; S6 = 381; S7 = 765 ; t6 = S6 – S5 = 381 – 189 = 192
t7 = S7 – S6 = 765 – 381 = 384
Ex.13 Three positive distinct numbers x, y, z are three terms of geometric progression in an order and the numbers x + y, y + z, z + x are three terms of arithmetic progression in that order. Prove that
xx . yy = xy . yz . zx.
Sol. Let x be first term of G.P. and y and z be the mth and nth of same G.P. respectively
⇒ tm = y = xrm - 1 and tn = z = x rn - 1, where r is a common ratio of G.P. ⇒ ...(1)
Now, we have y + z = x + y + (m - 1) d and z + x = x + y + (n - 1) d,
where id ia common difference of A.P. ⇒ From (1) and (2),
⇒ ⇒ y = z(z - x) /(z - y) . x(x - y)/(z - y)
⇒ y(z - y) = z(z - x) . x(x - y)
⇒ xx . yy . zz = xy . yz . zx
Ex.14 Using G.P. express form.
Sol. Let x = = 0.3333............. = 0.3 + 0.03 + 0.003 + 0.0003 + .............
=
= .
Let y = = 1.233333 = 1.2 + 0.03 + 0.003 + 0.0003 +................
= 1.2 + +................ = 1.2 +
.
Ex.15 The 1st, 2nd and 3rd terms of an arithmetic series are a, b and a2 where 'a' is negative. The 1st, 2nd and 3rd terms of a geometric series are a, a2 and b find the
(a) value of a and b
(b) sum of infinite geometric series if it exists. If no then find the sum to n terms of the G.P.
(c) sum of the 40 term of the arithmetic series.
Sol. a, b, a2 are in A.P. (a < 0) a, a2, b are in G.P.
(a) 2b = a + a2 ⇒ b = (a + 1) and a4 = ab, a3 = b since a < 0 [
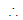
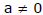 ]
]
a3 = (a + 1) ⇒ 2a2 - a - 1 = 0 ⇒ (2a + 1)(a - 1) = 0, a = 1 (rejected as a < 0) or a = -
⇒ a2 = ;
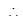 b = -
b = - = -
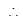 common difference b - a
common difference b - a 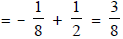
(b) common ratio r = ; r =
= -
;
Since | r | < 1 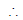 S∞ exists
S∞ exists
∴ S∞ = - = -
(c) S40 = 20 =
= × 109 =
=
Ex.16 In an arithmetic progression, the third term is 15 and the eleventh term is 55. An infinite geometric progression can be formed beginning with the eighth term of this A.P. and followed by the fourth and second term. Find the sum of this geometric progression upto n terms. Also compute S∞ if it exists.
Sol. Given a + 2d = 15 ....(1),
+ 10d = 55 ....(2)
solving (1) and (2)
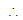 8d = 40 , d = 5 & a = 5
8d = 40 , d = 5 & a = 5
∴ t8 = 40 & t4 = 20 t2 = 10
hence the G.P. is 40, 20, 10, ....... ∞ ( | r | < 1) hence S∞ exists.
∴ S∞ = = 80
Sn = =
Ex.17 If the first 3 consecutive terms of a geometrical progression are the roots of the equation ,2x3 - 19x2 + 57x - 54 = 0 find the sum to infinite number of terms of G.P.
Sol. let the roots be 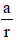 , a, ar
, a, ar
∴ a=
....(1),
a2 =
....(2),
a3=
= 27 ....(3)
∴ a = 3
from (1)
3(r2 + r + 1) =
⇒ 6r2 + 6r + 6 = 19r
⇒ 6r2 - 13r + 6 = 0
⇒ (2r - 3)(3r - 2) = 0
⇒ r = or
(rejected)
 Numbers are
Numbers are , a, ar
⇒ , 3, 2
S∞ = =
=
Ex.18 Let P = then find log0.01(P).
Sol. P = =
= = 102 = 100
 log0.01(P) = - 1
log0.01(P) = - 1
Ex.19 A positive number is such that its fractional part, its integral part and the number itself constitute the first three terms of a geometrical progression . Show that the nth term and the sum of the first n terms of the G.P. are, 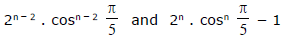 respectively.
respectively.
Sol. x ⇒ y, m, m + y in G.P. m2 = y (m + y)
⇒ y2 + my - m2 = 0
If y = put m = 1 ; y =
or
y = (not possible)
G.P. , 1 ,
.... Now proceed
Ex.20 One of the roots of the equation 2000x6 + 100x5 + 10x3 + x - 2 = 0 is of the form , where m is non zero integer and n and r are relatively prime natural numbers. Find the value of m + n + r.
Sol.
hence, m = – 1; n = 161; r = 40
m + n + r = 200
Ex.21 Suppose that a1, a2,........,an,......... is an A.P. Let Sk = a(k – 1) n + 1 + a(k – 1)n + 2 + ...... + akn . Prove that S1, S2,.... are in A.P. having common difference equal to n2 times the common difference of the A.P. a1, a2,.....
Sol. We have Sk = a(k – 1) n + 1 + a(k – 1)n + 2 + .... + a(k – 1)n + n
Now we have a(k – 1) n + 1 = a1 + (k – 1) nd;
a(k – 1) n + 2 = a1 + (k – 1) nd + d
a(k – 1) n + 3 = a1 + (k – 1) nd + 2d
-----------------------
and
[putting k + 1 in place of k] Hence, we have Sk + 1–Sk = n2d
which is a constant independent of k. This proves that the sequence (Sk) is an A.P. having common difference n2d.
Ex.22 In a G.P. if S1 , S2 & S3 denote respectively the sums of the first n terms , first 2 n terms and first 3 n terms , then prove that
Sol.
T P T S1 (S1 - S3) = S2 (S1 - S2)
Ex. 23 How many increasing 3-term geometric progressions can be obtained from the sequence 1, 2, 22, 23,....,2n ? (e.g., {22, 25 ,28} is a 3-term geometric progression for n ≥ 8.)
Sol. Let us start counting 3–term G.P.’s with common ratios 2, 22, 23,...
The 3–term G.P.’s with common ratio 2 are 1, 2,22; 2, 22, 23;.......; 2n – 2, 2n – 1, 2n.
Theyy are (n – 1) in number. The 3–term GP’s with common ratio 22 are
1, 22, 24; 2, 23, 25; ....... ; 2n – 4, 2n – 2, 2n
They are (n – 3) in number. Similarly we see that the 3–term GP’s with common ratio 23 are (n – 5) in number and so on. Thus the number of 3–term GP’s which can be formed from the sequence 1, 2, 22, 23,.....,2n is equal to S = (n – 1) + (n – 3) + (n – 5) +.........
Here the last term is 2 or 1 according as n is odd or even. If n is odd, then
S = (n – 1) + (n – 3) + (n – 5) + .... + 2
If n is even, then S = (n – 1) + (n – 3) + .... + 1 = n2/4
Hence the required number is (n2 – 1)/4 or n2/4 according as n is odd or even.
Ex.24 N = 2n – 1 (2n – 1) and (2n – 1) is a prime number.
1 < d1 < d2 < ..... < dk = N are the divisors of N. Show that
Sol. Let 2n – 1 = q
1, d1 d2 .... dk are divisors
1, 2, 22, ...., 2n–1, 2q, ...., 2n – 1 q respectively.
|
73 videos|264 docs|91 tests
|
FAQs on Geometric Progression (G.P) - Mathematics (Maths) Class 11 - Commerce
| 1. What is a geometric progression (G.P)? |  |
| 2. How do you find the common ratio in a geometric progression? |  |
| 3. What is the formula to find the nth term of a geometric progression? |  |
| 4. Can a geometric progression have a negative common ratio? |  |
| 5. How can geometric progressions be used in real-life situations? |  |

















