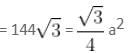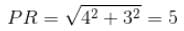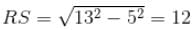This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Geometry (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Geometry
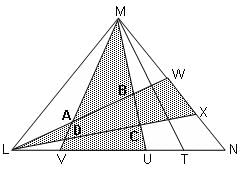
Try yourself:The area of triangle LMN is 120 square units. The shaded and unshaded regions have equal areas. If the area of triangle MVU is 1/3rd the area of triangle LMN, and the area of triangle LWX is 1/4th the area of triangle LMN, then find the area of quadrilateral ABCD. (Note: The figure is not drawn as per the scale.)
Explanation
Area of ΔMUV = (1/3) x Area of ΔLMN = 40 sq. units
Similarly, area of ΔLWX = (1/4) x 120 sq. units = 30 sq. units
Let the area of ABCD be x sq. units.
Then, area of the shaded region = 30 sq. units – x + 40 sq. units – x + x = 70 sq. units – x = Area of the unshaded region
∴ 70 sq. units – x = (½) × 120 sq. units = 60 sq.units
∴ x = 10 sq. units
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:A wheel rests against the edge of a pavement as shown below. The height of the pavement is 3 m and the distance of the point where the wheel touches the ground from the point where the wheel touches the edge of the pavement is 5 m. Find the radius of the wheel.
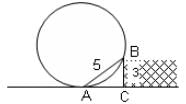
Explanation
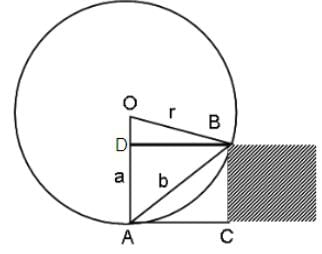
Draw BD || AC to cut OA at D.
In triangle ABC,
32 + AC2 = 52
AC = 4 m
Let radius = r.
OD2 + DB2 = OB2
DB = AC
DB2 = r2 - (r - a)2
42 = 2ar - a2 (where a = 3)
16 + 9 = 2 x 3 x r
or, r = (25/6) m
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:A circle is inscribed in a quadrant of a bigger circle, as shown in the figure below.
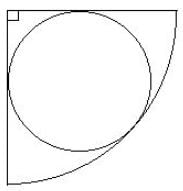
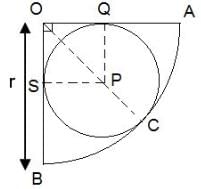
If the radius of the smaller circle is 2 units, what is the radius of the bigger circle?
Explanation
PQ = PS = 2
⇒ OQ = 2 [∵ ΔOQP ≅ ΔOSP]
Let OA = r
OP = (OC - PC) = r - 2
Also, (OP)2 = 2(OQ)2
(r - 2)2 = 2(2)2
⇒ r2 + 4 - 4r = 8
⇒ r2 - 4r - 4 = 0
⇒ r = 2(1 +√2) = 2(√2 + 1)
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:Two circles are placed in an equilateral triangle as shown in the figure. What is the ratio of the area of the smaller circle to that of the equilateral triangle
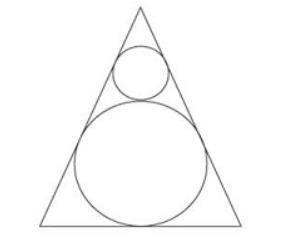
Explanation


Hence option c is correct
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:In the figure (not drawn to scale), rectangle ABCD is inscribed in a circle with centre at O. The length of side AB is greater than that of side BC. The ratio of the area of the circle to the area of the rectangle ABCD is π :. The line segment DE intersects AB at E such that ∠ODC = ∠ADE.
What is the ratio of AE : AD?
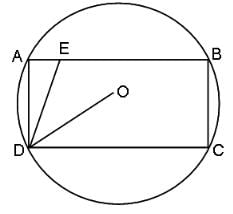
Explanation
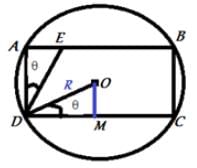
Let the radius of the circle be 'R' and ∠ODC = ∠ADE = θ.
If OM is drawn perpendicular to DC,
DM = R cos θ
OM = R sin θ
Length of rectangle ABCD,
AB = CD = 2DM = 2R cos θ
AD = BC = 2OM = 2R sin θ
Area of rectangle = AB(BC) = 2R cos θ x 2R sin θ = 2R² sin2θ
Area of circle = πR²
According to the question,
πR² : 2R² sin 2θ = π : √3
⇒ sin 2θ = √2 = sin 60°
θ = 30°
In triangle ADE, tan θ = AE/AD
AE : AD = tan 30° = 1 : √3
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:In the figure, the rectangle at the corner measures 10 cm x 20 cm. One corner of the rectangle is also a point on the circumference of the circle. What is the radius of the circle?
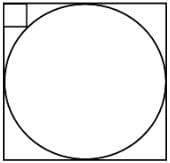
Explanation
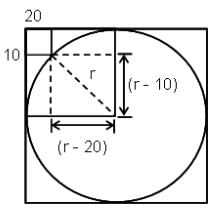
Let the radius of the circle be `r` cm.
∴ We get (r - 20)2 + (r - 10)2 = r2
∴ r2 - 40r + 400 + r2 - 20r + 100 = r2
∴ r2 - 60r + 500 = 0
∴ r = 10 cm or r = 50 cm
But, r cannot be 10 cm.
∴ r = 50 cm
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:The area of an equilateral triangle DRS is 144√3 sq. cm. If P is the centre of the circle, find the area of quadrilateral DRPS in the given figure.
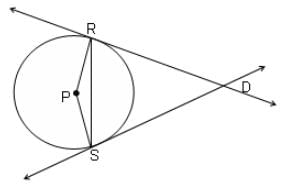
Explanation
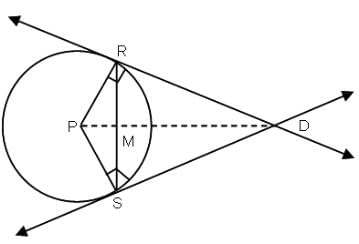
As shown in the figure, area of equilateral triangle
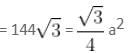
(a represents the length of side of an equilateral triangle)
a = 24 cm
In triangle RDP,
∠RDP = 30°
cos 30° = RD/PD = 24/PD
PD = 16√3 cm
Area of quadrilateral RDSP

192√3 sq. cm2
Report a problem
Question for Practice Questions Level 3: Geometry
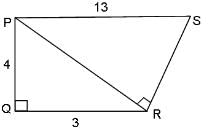
Try yourself:What is the area of quadrilateral PQRS?
Explanation
As shown in the figure, Area of quadrilateral PQRS = Area of triangle PQR + Area of triangle PRS … (1)
Both these triangles are right-angled triangles.
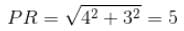
Area of triangle PQR = (1/2) x 4 x 3 = 6 sq. units
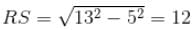
Area of triangle PRS = (1/2) x 12 x 5 = 30 sq. units
Area of quadrilateral PQRS = 6 + 30 = 36 sq. units
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:A, B, C, D, E ........ Z are the points marked on the circumference of a circle equidistantly. What can be the maximum number of triangles which can be formed using three points as vertices such that their circumcentre lies on one of the sides of a triangle?
Explanation
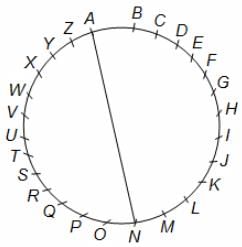
Circumcentre will lie on one of the sides if the triangle is a right-angled triangle.
So, two of the vertices of the triangle will lie on a diameter of the circle.
So, the points must be equidistant to maximise the number of such triangles.
Let AN be one such chosen diameter and hence, one side of a triangle.
It is to be noted that there will be 13 such diameters possible.
So, third vertex of the triangle can be chosen from any of the other 24 points left (other 24 points leaving A and N).
Possible total number of such triangles = 13 × 24 = 312.
Report a problem
Question for Practice Questions Level 3: Geometry
Try yourself:In the given figure, O is the centre of the circle and AE is a diameter. If AB = BC and ∠BFC = 25°, find the value of ∠ABC.
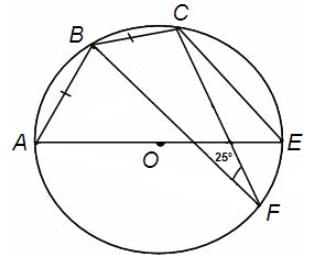
Explanation
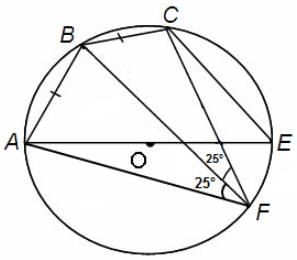
Angles subtended by equal chords are equal.
∠AFB = 25° = ∠BFC
In the cyclic quadrilateral ABCF,
∠AFC = 25° + 25° = 50°
∠ABC = 180° - 50° = 130° (because the sum of opposite angles of a cyclic quadrilateral is 180°)
Report a problem