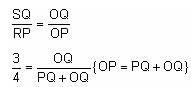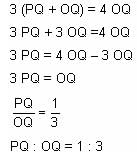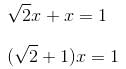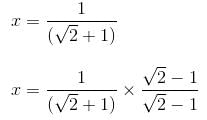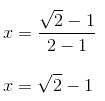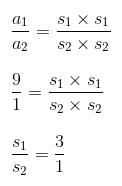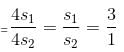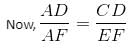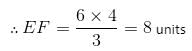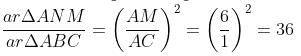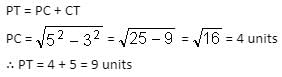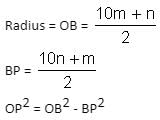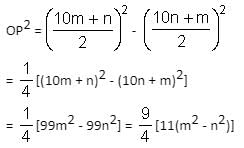This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Geometry (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Geometry - 1
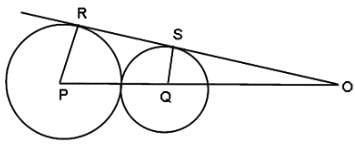
Try yourself:In the adjoining figure, I and II are circles with centres P and Q, respectively. The two circles touch each other and have a common tangent that touches them at points R and S, respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the ratio 4 : 3. It is also known that the length of PQ is 28 cm.
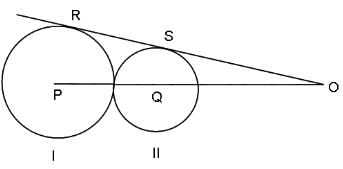
What is the ratio of the length of PQ to that of QO?
Explanation
Let the diameter of circle I and II be 4x and 3x, respectively.
ΔOSQ is similar to ΔORP by AA criteria.
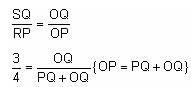
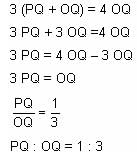
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:Two perpendicular lines that intersect each other at the centre of a circle of radius 1 unit divides the circle into four parts. A smaller circle is inscribed in one of those parts as shown in the figure below. What is the radius of the smaller circle?

Explanation
Let x denote the radius of the smaller circle. The figure shows the lengths marked to the right as follows.
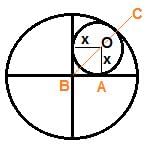
Here,
BO2 = AB2 + AO2
BO2 = x2 + x2
BO = √2x
BO + OC = 1
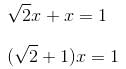
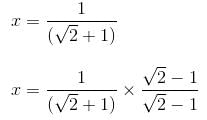
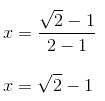
Hence, this is the correct answer.
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:If the ratio of areas of two squares is 9 : 1, then the ratio of their perimeters will be
Explanation
Let area of the first square be a1, whose side is s1.
Let area of the second square be a2, whose side is s2.
Then,
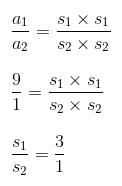
So, required ratio of perimeter
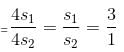
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:In the given figure, if PM and PN are tangents to the circle with centre Q, radius = 7 cm and PM = 7 cm, then what is the length of PQ?
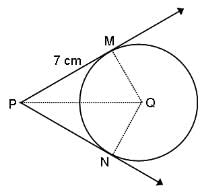
Explanation

PM is a tangent and MQ is the radius.
⇒ QM perpendicular to PM
⇒ PMQ is a right-angled Δ.
PQ2 = PM2 + MQ2 (By Pythagoras Theorem)
PQ2 = (7)2 + (7)2 = 2(7)2
PQ2 = 98
PQ = 7√2 cm
Report a problem
Question for Practice Questions Level 1: Geometry - 1
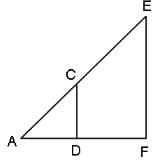
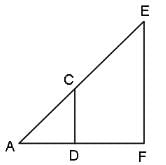
Try yourself:CD is parallel to EF. AD = DF, CD = 4 units and DF = 3 units. What is the measure of EF?
Explanation
In ΔADC and ΔAFE:
∠A = ∠A {Common}
AD = DF {Given}
∠ADC = ∠AFE
{Corresponding angles between two || lines}
Hence, ΔADC is similar to ΔAFE.
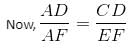
We know: AF = AD + DF = 3 + 3 = 6 units
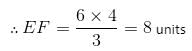
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:ΔABC, ΔCDE, ΔEFG, ΔGHI, ΔIJK and ΔKLM are congruent to one another and similar to ΔANM. What is the ratio of the area of ΔANM to the area of ABC?
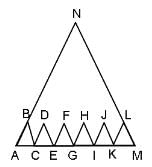
Explanation
Since all small triangles are congruent, AC = CE = EG = GI = IK = KM and 6AC = AM.
Now, as ΔANM ~ ΔABC,
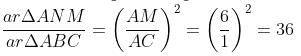
Required Ratio = 36 : 1
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:The figure given below has 2 circles with centers A and B.What is the measure of ∠APT?
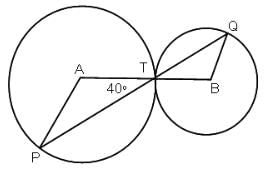
Explanation
Since AT = AP, (Radii)
∴ ∠APT = ∠ATP = 40°
ΔAPT is an isosceles Δ, i.e. with AP = AT and the angles subtended by them will be the same.
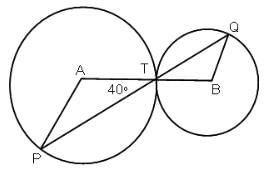
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:ABCD is a cyclic trapezium with segments AB and DC parallel to each other. If ∠ABC = 80°, then what is the measure of the angle subtended by major arc ABC at the centre?
Explanation
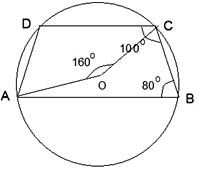
Angle subtended by the minor arc ADC at centre = 2 × (∠ABC) = 160°
Angle subtended by the complementary major arc ABC at centre = (360 - 160)° = 200°
Report a problem
Question for Practice Questions Level 1: Geometry - 1
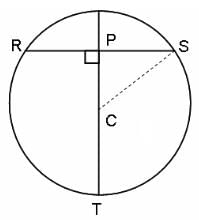
Try yourself:If C is the centre of the following circle, RS = 6 units and SC = 5 units, then what is the length of PT?
Explanation
RS = 6 units, SC = 5 units = CT
RP = 6/2 = 3 units = PS, as perpendicular from the centre to chord divides the chord into 2 equal parts.
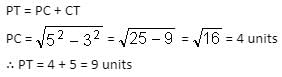
Report a problem
Question for Practice Questions Level 1: Geometry - 1
Try yourself:The chord AB is perpendicular to the diameter MN at P. The lengths MN and AB are two-digit integral numbers and the length AB is obtained by reversing the digits of the length MN. The length OP is a non-zero rational number. Find the diameter of the circle.
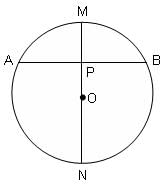
Explanation
Put MN = 10m + n
AB = 10n + m
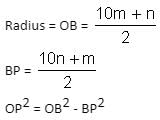
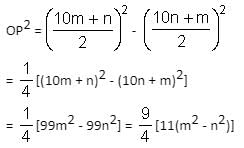

As OP is rational, so 11 must divide (m + n)(m - n) and m and n are single digit numbers.
Hence, m = 6, n = 5.
Therefore, diameter MN = 10(6) + 5 = 65 units
Report a problem