Geometry: Solved Examples- 2 | CSAT Preparation - UPSC PDF Download
Question 11: What is the ratio of longest diagonal to the shortest diagonal in a regular octagon?
A. √3 : 1
B. 2 : 1
C. 2 : √3
D. √2 : 1
Answer. √2 : 1
Explanation.
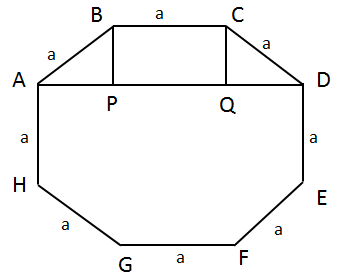
Consider regular octagon ABCDEFGH
Its longest diagonal would be AE or BF or CG or DH.
Let us try to find out AE.
Join AD and draw BP ⊥ AD and CQ ⊥ AD.
PQ = a
AP = QD
a2 = BP2 + AP2 => a2 = 2 AP2 {since BP=AP}
a = √2AP => AP = a/(√2)
AD =AP + PQ + QD = a/(√2) + a + a/(√2)
⇒ a + a√2
AE2 = AD2 + DE2
AE2 = (a + a√2) 2 + a2
AE2 = (a2 + 2 * a * √2 + 2a2) + a2
AE2 = a2 (1 + 2√2 + 2) + a2
⇒ a2 (4 + 2√2)
Shortest diagonal = AC or CE
AC2 = AB2 + BC2 – 2AB × BC cos135 degree
(Alternatively, we can deduce this using AC2 = AQ2 + QC2. We use cosine rule just to get some practice on a different method.)
= a2 + a2 – 2a2 * ((−1)/√2)
= 2a2 + √2a2
= a2 (2 + √2)
AE2 = a2 (4 + 2√2)
AE2/AC2 = a2 (4 + 2√2) / a2 (2 + 2√2) = 2
AE / AC = √2
Remember, for a regular octagon.
Each internal angle = 135 degrees.
Each external angle = 45 degrees.
So, we get a bunch of squares and isosceles right–angled △s if we draw diagonals.
A regular hexagon breaks into equilateral triangles. A regular octagon breaks into isosceles right angled triangles.
The question is "What is the ratio of longest diagonal to the shortest diagonal in a regular octagon?"
Hence, the answer is √2 : 1
Choice D is the correct answer.
Question 12: Find the altitude to side AC of triangle with side AB = 20 cm, AC = 20 cm, BC = 30 cm.
A. 10√7
B. 8√7
C. 7.5√7
D. 15√7
Answer. 7.5√7
Explanation.
This is an isosceles triangle. So, let us find the altitude to BC first.
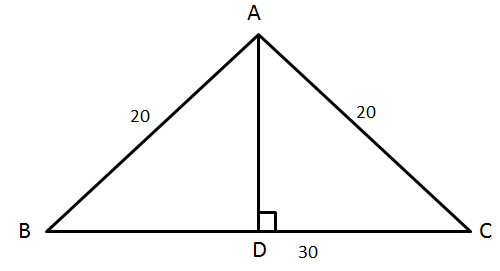
Altitude to BC bisects BC as △ADB and △ADC are congruent.
{RHS congruence; AD is common, AB = AC}
DC = 15
AD2 + DC 2 = AC2
AD2 + 15 2 = 202
AD2 = 400 - 225
AD2 = 175
AD = 5√7
Area of the triangle 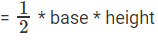
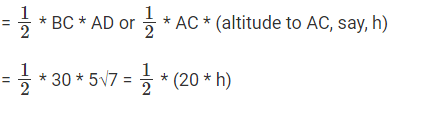
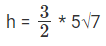
h = 7.5√7
The question is " Find the altitude to side AC of triangle with side AB = 20 cm, AC = 20 cm, BC = 30 cm."
Hence, the answer is 7.5√7.
Choice C is the correct answer.
Question 13: ABCDEF is a regular hexagon inscribed inside a circle. If the shortest diagonal of the hexagon is of length 3 units, what is the area of the shaded region.
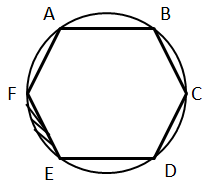
A. 1/6(3π − (9√3)/2)
B. 1/6(2π − (6√3)/2)
C. 1/6(3π − (8√3)/2)
D. 1/6(6π − (15√3)/2)
Answer. 1/6(3π − (9√3)/2)
Explanation.
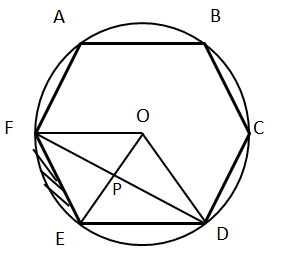
Let side of regular hexagon be a.
The shortest diagonal will be of length a√3. Why?
A regular hexagon is just 6 equilateral triangles around a point. The shortest diagonal is FD.
FD = FP + PD
△FOE is equilateral and so is △ EOD.
Diagonal FD can be broken as FP + PD, both of which are altitude of equilateral s.
FP = (√3a)/2
FD = √3a = shortest diagonal
The question tells us that the shortest diagonal measures 3 cm.
√3a = 3 ⇒ a = √3
Radius of circle = √3
Area of hexagon = (√3a2)/4 * 6
Area of circle – area of hexagon = π (√3)2 − √3/4 * (√3)2 * 6
= 3π − (9√3)/2
Area of shaded region = 1/(6) (area(circle) – area(hexagon))
= 1/(6)(3π − (9√3)/2)
The question is "what is the area of the shaded region?"
Hence, the answer is 1/(6)(3π − (9√3)/2)
Choice A is the correct answer.
Question 14: A circle of radius 5 cm has chord RS at a distance of 3 units from it. Chord PQ intersects with chord RS at T such that TS = 1/3 of RT. Find minimum value of PQ.
A. 6√3
B. 4√3
C. 8√3
D. 2√3
Answer. 4√3
Explanation.
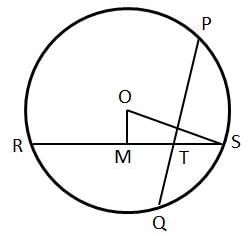
OM = 3, OS = 5
MS = 4 = RM {Using Pythagoras theorem}
⇒ RS = 8 cms
TS = 1/3 of RT
TS = 1/4 of RS
TS = 2 cms
RT * TS = PT * TQ
{Intersecting Chords theorem: When there are two intersecting chords, the product of the rectangle formed by the segments of one chord is equal to the product of the rectangle formed by the segments of the other.}
6 × 2 = PT * TQ
PT * TQ = 12
By AM – GM inequality, (PT+TQ)/2 ≥ √(PT * TQ)
(PT+TQ)/2 ≥ √12
PT + TQ ≥ 2√12
⇒ PQ ≥ 2√12
Or PQ ≥ 4√3
Minimum PQ = 4√3
The question is " Find minimum value of PQ."
Hence, the answer is 4√3.
Choice B is the correct answer.
Question 15: Triangle has perimeter of 6 + 2√3 . One of the angles in the triangle is equal to the exterior angle of a regular hexagon another angle is equal to the exterior angle of a regular 12-sided polygon. Find area of the triangle.
A. 2√3
B. √3
C. √3/2
D. 3
Answer. 2√3
Explanation.
Given, Perimeter = 6 + 2√3
One of the angles in the triangle is equal to the exterior angle of a regular hexagon which is equal to 60°
Another angle is equal to the exterior angle of a regular 12-sided polygon = 30°.
From this we can deduce that the other angle is equal to 90°.
The property of a 60-30-90 triangle is that, the sides are in the ratio √3x, x and 2x.
Therefore, Perimeter is sum of all sides = x(3+ √3)= 6 + 2√3 .
⇒ x = (6 + 2√3)/(3+ √3) = 2.
Therefore, the sides are 2√3, 2 and 4.
Area of a Right Triangle = 1/2 * Product of Perpendicular sides = 1/2 * 2 * 2√3 = 2√3 .
The question is "Perimeter of a △ with integer sides is equal to 15. How many such triangles are possible?"
Hence, the answer is 2√3.
Choice A is the correct answer.
Question 16: Area of a Rhombus of perimeter 56 cms is 100 sq cms. Find the sum of the lengths of its diagonals.
A. 33.40
B. 34.40
C. 31.20
D. 32.30
Answer. 34.40
Explanation.
Given, Perimeter = 56 and area = 100.
Let the side of the rhombus be “a”, then 4a = 56 => a = 14.
Area of Rhombus = Half the product of its diagonals. Let the diagonals be d1 and d2 respectively.
1/2 * d1 * d2 = 100 => d1 * d2 = 200. By Pythagoras theorem, (d1)2 + (d2)2 = 4a2
⇒ (d1)2 + (d2)2 = 4*196 = 784.
(d1)2 + (d2)2 + 2d1 * d2 = (d1+ d2)2 = 784 +2*200 = 1184 => (d1+ d2) = √1184 = 34.40
Therefore, sum of the diagonals is equal to 34.40 cm .
The question is " Find the sum of the lengths of its diagonals."
Hence, the answer is 34.40.
Choice B is the correct answer.
Question 17: Rhombus has a perimeter of 12 and one angle = 120°. Find its area.
A. 9 * (√3)/2
B. 3 * (√3)/2
C. 9 * √3
D. 18 * √3
Answer. 9 * (√3)/2
Explanation.
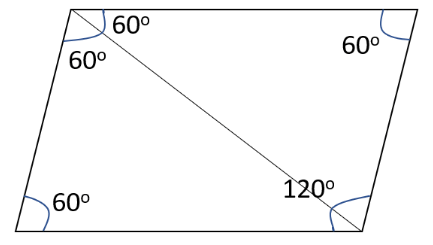
Perimeter = 12.
Let the side of the rhombus be “a”, then 4a = 12 => a = 3.
One angle = 120°.
Adjacent angles of a rhombus are supplementary. Therefore, the other angle = 60°.
Diagonals of a rhombus bisect each other, therefore, ∠DAC = 60° ∠DCA =60° ∠BAC =60°
Therefore, Triangle DAC and BAC are equilateral triangles.
Therefore, Area of Rhombus = 2 * Area of the Equilateral Triangle
= 2 * (√3/4) * a2 = (√3/2) * 9 = 9 * (√3/2).
The question is " Find the area of the rhombus"
Hence, the answer is 9 * (√3/2).
Choice A is the correct answer.
Question 18: Circle with center O and radius 25 cms has a chord AB of length of 14 cms in it. Find the area of triangle AOB
A. 144 cm2
B. 121 cm2
C. 156 cm2
D. 168 cm2
Answer. 168 cm2
Explanation.
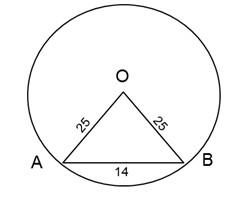
Given :
Radius of the circle = 25 cm
Center is O
Length of Chord AB = 14 cm
Therefore, △ AOB will be an isosceles triangle with 2 sides OA and OB as 25 cm and side AB as 14 cm.
For an isosceles triangle with the equal sides as 'a' and base as 'b' then
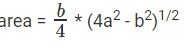
Hence Area 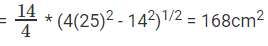
The question is "Find the area of triangle AOB."
Hence, the answer is 168 cm2.
Choice D is the correct answer.
Question 19: Two mutually perpendicular chords AB and CD intersect at P. AP = 4, PB = 6, CP = 3. Find radius of the circle.
A. 31.25(1/2)
B. 37.5(1/2)
C. 26(1/2)
D. 52(1/2)
Answer. 31.25(1/2)
Explanation.
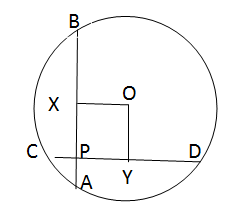
When 2 chords AB and CD intersect at P then AP * PB = CP * PD
Hence 4 * 6 = 3 * PD
Thus, PD = 8
Now AB = AP + PB = 10
And CD = CP + PD
Thus, CD = 11
Consider the circle with center O.
Drop a perpendicular from O to chord AB and CD.
This will bisect the chords at X and Y i.e AX=XB and CY = YD.
Here AX = AP + PX i.e 5 = 4 + PX
PX = 1
Similarly, since CD = 11, PY+CP+YD = 11,
⇒ PY = 11-3-5.5 = 2.5.
PY = OX and PX = OY.
So, PXOY will from a rectangle as seen in the figure.
Now consider the triangle BOX, it is a right triangle where OB is the radius.
XB = 5, OX = 2.5
Then OB = ( OX2 + XB2 )1/2 OB = 31.251/2 Thus radius = 31.251/2 The radius can also be found out using the triangle YOD.
The question is "Find radius of the circle."
Hence, the answer is 31.251/2.
Choice A is the correct answer.
Question 20: Triangle ABC has angles A = 60° and B = 70°. The incenter of this triangle is at I. Find angle BIC.
A. 90°
B. 130°
C. 80°
D. 120°
Answer. 120°
Explanation.
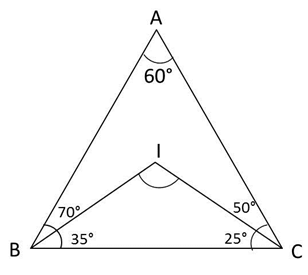
A + B + C = 180 in a triangle
Hence C = 180 – 130 = 50°
Incenter is the meeting point of angle bisectors. BIC will form a triangle.
In this triangle B = 35, C = 25
Hence BIC or I = 180 – (35 + 25) = 120°
The question is "Find angle BIC."
Hence, the answer is 120°.
Choice D is the correct answer.
|
207 videos|276 docs|138 tests
|
FAQs on Geometry: Solved Examples- 2 - CSAT Preparation - UPSC
| 1. What are the different types of angles in geometry? |  |
| 2. How can I determine the area of a triangle? |  |
| 3. What is the Pythagorean theorem? |  |
| 4. How can I calculate the circumference of a circle? |  |
| 5. What is the difference between a polygon and a polyhedron? |  |






















