Grand - Canonical Ensembles and Partition Functions - CSIR-NET Physical Sciences | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Two simple examples
Here we consider two examples with the simplest structures of energy levels to illustrate the use of microcanonical and canonical distributions.
Two-level system
Assume levels 0 and ε. we considered two-level system in the microcanonical approach calculating the number of ways one can distribute L = E = ε portions of energy between N particles and obtaining

 The temperature in the microcanonical approach is as follows.
The temperature in the microcanonical approach is as follows.

The entropy as a function of energy is drawn on the Figure.

Indeed, entropy is zero at E = 0, N ε when all the particles are in the same state. The entropy is symmetric about E = N ε/2. We see that when E > N ε/2 then the population of the higher level is larger than of the lower one (inverse population as in a laser) and the temperature is negative.
Negative temperature may happen only in systems with the upper limit of energy levels and simply means that by adding energy beyond some level we actually decrease the entropy i.e. the number of accessible states. Available (non-equilibrium) states lie below the S (E ) plot, notice that for the right (negative-temperature) part the entropy maximum corresponds to the energy maximum as well. A glance on the figure also shows that when the system with a negative temperature is brought into contact with the thermostat (having positive temperature) then our system gives away energy (a laser generates and emits light) decreasing the temperature further until it passes through infinity to positive values and eventually reaches the temperature of the thermostat. That is negative temperatures are actually "hotter" than positive.
Let us stress that there is no volume in S (E, N ) that is we consider only subsystem or only part of the degrees of freedom. Indeed, real particles have kinetic energy unbounded from above and can correspond only to positive temperatures [negative temperature and infinite energy give infinite Gibbs factor exp(-E /T )]. Apart from laser, an example of a two-level system is spin 1/2 in the magnetic field H . Because the interaction between the spins and atom motions (spin-lattice relaxation) is weak then the spin system for a long time (tens of minutes) keeps its separate temperature and can be considered separately. Let us derive the generalized force M that corresponds to the magnetic field and determines the work done under the change of magnetic field. dE = T dS - M dH . Since the pro jection of every magnetic moment on the direction of the field can take two values  then the magnetic energy of the particle is
then the magnetic energy of the particle is  The force is calculated according to (34) and is called magnetization (or magnetic moment of the system).
The force is calculated according to (34) and is called magnetization (or magnetic moment of the system).

The derivative was taken at constant entropy that is at constant populations N+ and N-. Note that negative temperature for the spin system corresponds to the magnetic moment opposite in the direction to the applied magnetic field. Such states are experimentally prepared by a fast reversal of the magnetic field. We can also define magnetic susceptibility.

At weak fields and positive temperature,  gives the formula for the so-called Pauli paramagnetism
gives the formula for the so-called Pauli paramagnetism
 (21)
(21)
Para means that the majority of moments point in the direction of the external field. This formula shows in particular a remarkable property of the spin system. adiabatic change of magnetic field (which keeps N+, N- and thus M ) is equivalent to the change of temperature even though spins do not exchange energy. One can say that under the change of the value of the homogeneous magnetic field the relaxation is instantaneous in the spin system.
This property is used in cooling the substances that contain paramagnetic impurities. Note that the entropy of the spin system does not change when the field changes slowly comparatively to the spin-spin relaxation and fast comparatively to the spin-lattice relaxation.
To conclude let us treat the two-level system by the canonical approach where we calculate the partition function and the free energy.

We can now re-derive the entropy as  and derive the (mean) energy and specific heat.
and derive the (mean) energy and specific heat.


Note that (24) is a general formula which we shall use in the future. Specific heat turns into zero both at low temperatures (too small portions of energy are "in circulation") and in high temperatures (occupation numbers of two levels already close to equal).
Harmonic oscillators
Small oscillations around the equilibrium positions (say, of atoms in the lattice or in the molecule) can be treated as harmonic and independent.
The harmonic oscillator is described by the Hamiltonian

We start from the quasi-classical limit,  when the single-oscillator partition function is obtained by Gaussian integration.
when the single-oscillator partition function is obtained by Gaussian integration.

We can now get the partition function of N independent oscillators as Z(T, N) = 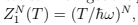 the free energy
the free energy  and the mean energy from (24): E = NT — this is an example of the equipartition (every oscillator has two degrees of freedom with T/2 energy for each)2 . The thermodynamic equations of state are
and the mean energy from (24): E = NT — this is an example of the equipartition (every oscillator has two degrees of freedom with T/2 energy for each)2 . The thermodynamic equations of state are 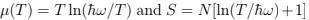 while the pressure is zero because there is no volume dependence. The specific heat CP = CV = N.
while the pressure is zero because there is no volume dependence. The specific heat CP = CV = N.
Apart from thermodynamic quantities one can write the probability distribution of coordinate which is given by the Gibbs distribution using the potential energy.

Using kinetic energy and simply replacing q → p/ω one obtains a similar formula  which is the Maxwell distribution.
which is the Maxwell distribution.
For a quantum case, the energy levels are given by 
The single-oscillator partition function


where one sees the contribution of zero quantum oscillations and the breakdown of classical equipartition. The specific heat is as follows. CP = CV = 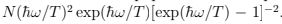 Comparing with (26) we see the same behavior at
Comparing with (26) we see the same behavior at 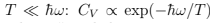 because “too small energy portions are in circulation" and they cannot move system to the next level.
because “too small energy portions are in circulation" and they cannot move system to the next level.
At large T the specific heat of two-level system turns into zero because the occupation numbers of both levels are almost equal while for oscillator we have classical equipartition (every oscillator has two degrees of freedom so it has T in energy and 1 in CV ).
Quantum analog of (29) must be obtained by summing the wave functions of quantum oscillator with the respective probabilities.

Here a is the normalization factor. Straightforward (and beautiful) calculation of (31) can be found in Landau & Lifshitz Sect. 30. Here we note that the distribution must be Gaussian  where the meansquare displacement
where the meansquare displacement  can be read from the expression for energy so that one gets.
can be read from the expression for energy so that one gets.

At  it coincides with (29) while at the opposite (quantum) limit gives
it coincides with (29) while at the opposite (quantum) limit gives  which is a purely quantum formula
which is a purely quantum formula  for the ground state of the oscillator.
for the ground state of the oscillator.
See also Pathria Sect. 3.7 for more details.
Entropy
By definition, entropy determines the number of available states (or, classically, phase volume). Assuming that system spends comparable time in different available states we conclude that since the equilibrium must be the most probable state it corresponds to the entropy maximum. If the system happens to be not in equilibrium at a given moment of time [say, the energy distribution between the subsystems is different from the most probable Gibbs distribution (16)] then it is more probable to go towards equilibrium that is increasing entropy. This is a microscopic (probabilistic) interpretation of the second law of thermodynamics formulated by Clausius in 1865. Note that the probability maximum is very sharp in the thermodynamic limit since exp(S ) grows exponentially with the system size. That means that for macroscopic systems the probability to pass into the states with lower entropy is so vanishingly small that such events are never observed.
Dynamics (classical and quantum) is time reversible. Entropy growth is related not to the tra jectory of a single point in phase space but to the behavior of finite regions (i.e. sets of such points). Consideration of finite regions is called coarse graining and it is the main feature of stat-physical approach responsible for the irreversibility of statistical laws. The dynamical background of entropy growth is the separation of tra jectories in phase space so that tra jectories started from a small finite region fill larger and larger regions of phase space as time proceeds. On the figure, one can see how the black square of initial conditions (at the central box) is stretched in one (unstable) direction and contracted in another (stable) direction so that it turns into a long narrow strip (left and right boxes). Rectangles in the right box show finite resolution (coarse-graining). Viewed with such resolution, our set of points occupies larger phase volume (i.e. corresponds to larger entropy) at  than at t = 0. Time reversibility of any particular tra jectory in the phase space does not contradict the time-irreversible filling of the phase space by the set of tra jectories considered with a finite resolution.
than at t = 0. Time reversibility of any particular tra jectory in the phase space does not contradict the time-irreversible filling of the phase space by the set of tra jectories considered with a finite resolution.
By reversing time we exchange stable and unstable directions but the fact of space filling persists.

The second law of thermodynamics is valid not only for isolated systems but also for systems in the (time-dependent) external fields or under external conditions changing in time as long as there is no heat exchange. If temporal changes are slow enough then the entropy does not change i.e. the process is adiabatic. Indeed, if we have some parameter λ(t) slowly changing with time then positivity of  requires that the expansion of
requires that the expansion of  starts from the second term,
starts from the second term,

We see that when dλ=dt goes to zero, entropy is getting independent of λ.
That means that we can change λ (say, volume) by finite amount making the entropy change whatever small by doing it slow enough.
During the adiabatic process the system is assumed to be in thermal equilibrium at any instant of time (as in quasi-static processes defined in thermodynamics). Changing λ (called coordinate) one changes the energy levels Ea and the total energy. Respective force (pressure when λ is volume, magnetic or electric moments when λ is the respective field) is obtained as the average (over the equilibrium statistical distribution) of the energy derivative with respect to λ and is equal to the derivative of the thermodynamic energy at constant entropy because the probabilities wa = 1/  does not change.
does not change.

Here  is the microscopic Hamiltonian while E (S, λ, . . .) is the thermodynamic energy. Note that in an adiabatic process all wa are assumed to be constant i.e. the entropy of any subsystem us conserved. This is more restrictive than the condition of reversibility which requires only the total entropy to be conserved. In other words, the process can be reversible but not adiabatic. See Landau & Lifshitz for more details.
is the microscopic Hamiltonian while E (S, λ, . . .) is the thermodynamic energy. Note that in an adiabatic process all wa are assumed to be constant i.e. the entropy of any subsystem us conserved. This is more restrictive than the condition of reversibility which requires only the total entropy to be conserved. In other words, the process can be reversible but not adiabatic. See Landau & Lifshitz for more details.
The last statement we make here about entropy is the third law of thermodynamics (Nernst theorem) which claims that S → 0 as T → 0. A standard argument is that since stability requires the positivity of the specific heat cv then the energy must monotonously increase with the temperature and zero temperature corresponds to the ground state. If the ground state is non-degenerate (unique) then S = 0. Since generally the degeneracy of the ground state grows slower than exponentially with N , then the entropy per particle is zero in the thermodynamic limit. While this argument is correct it is relevant only for temperatures less than the energy difference between the first excited state and the ground state. As such, it has nothing to do with the third law established generally for much higher temperatures and related to the density of states as function of energy. We shall discuss it later considering Debye theory of solids. See Huang for more details.
Grand canonical ensemble
Let us now repeat the derivation we done in Sect. 1.3 but in more detail and considering also the fluctuations in the particle number N . The probability for a subsystem to have N particles and to be in a state EaN can be obtained by expanding the entropy of the whole system. Let us first do the expansion up to the first-order terms as in (10,11)
 canonical potential which can be expressed through the grand partition function
canonical potential which can be expressed through the grand partition function

The grand canonical distribution must be equivalent to canonical if one neglects the fluctuations in particle numbers. Indeed, when we put  the thermodynamic relation gives
the thermodynamic relation gives  so that (35) coincides with the canonical distribution
so that (35) coincides with the canonical distribution 
To describe fluctuations one needs to expand further using the second derivatives  (which must be negative for stability).
(which must be negative for stability).
That will give Gaussian distributions of  straightforward way to find the energy variance
straightforward way to find the energy variance  is to differentiate with respect to β the identity
is to differentiate with respect to β the identity  For this purpose one can use canonical distribution and get
For this purpose one can use canonical distribution and get

Since both and CV are proportional to N then the relative fluctuations are small indeed:
and CV are proportional to N then the relative fluctuations are small indeed:  In what follows (as in the most of what preceded) we do not distinguish between E and
In what follows (as in the most of what preceded) we do not distinguish between E and 
Let us now discuss the fluctuations of particle number. One gets the probability to have N particles by summing (35) over a:  F (T , V , N )] where F (T , V , N ) is the free energy calculated from the canonical distribution for N particles in volume V and temperature T . The mean value
F (T , V , N )] where F (T , V , N ) is the free energy calculated from the canonical distribution for N particles in volume V and temperature T . The mean value  is determined by the extremum of probability:
is determined by the extremum of probability:  The second derivative determines the width of the distribution over N that is the variance:
The second derivative determines the width of the distribution over N that is the variance:

Here we used the fact that 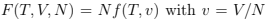 and substituted the derivatives calculated at fixed
and substituted the derivatives calculated at fixed 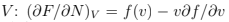
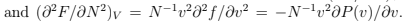 As we discussed in Thermodynamics,
As we discussed in Thermodynamics, 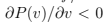 for stability. We see that generally the fluctuations are small unless the isothermal compressibility is close to zero which happens at the first-order phase transitions. Particle number (and density) strongly fluctuate in such systems which contain different phases of different densities. Note that any extensive quantity
for stability. We see that generally the fluctuations are small unless the isothermal compressibility is close to zero which happens at the first-order phase transitions. Particle number (and density) strongly fluctuate in such systems which contain different phases of different densities. Note that any extensive quantity  which is a sum over independent subsystems
which is a sum over independent subsystems have a small relative fluctuation:
have a small relative fluctuation: 
FAQs on Grand - Canonical Ensembles and Partition Functions - CSIR-NET Physical Sciences - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is the grand canonical ensemble? |  |
| 2. What is the partition function in the grand canonical ensemble? |  |
| 3. How is the partition function related to the probability of finding a particular state in the grand canonical ensemble? |  |
| 4. What is the significance of the chemical potential in the grand canonical ensemble? |  |
| 5. How can the grand canonical ensemble be applied to real-world systems? |  |

|
Explore Courses for Physics exam
|

|

















