Graph Searching | Algorithms - Computer Science Engineering (CSE) PDF Download

Breadth First Search or BFS for a Graph

Breadth First Traversal (or Search) for a graph is similar to Breadth First Traversal of a tree (See method 2 of this post). The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For simplicity, it is assumed that all vertices are reachable from the starting vertex.
For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Breadth First Traversal of the following graph is 2, 0, 3, 1.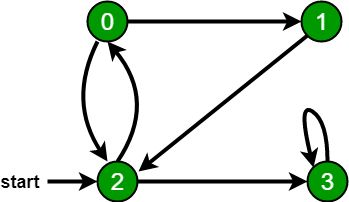

Following are the implementations of simple Breadth First Traversal from a given source.
The implementation uses adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes and queue of nodes needed for BFS traversal.

• C++
  
  
  
  
• Java
  
  
  
• Python3
  
  
  
• C#
  
  
  

Output:
Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1

Illustration:

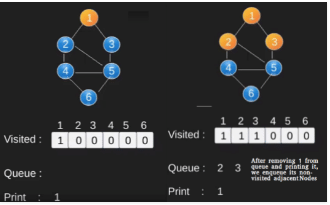
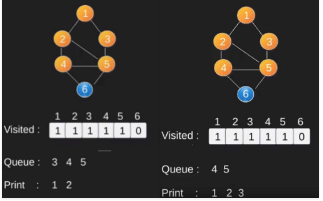
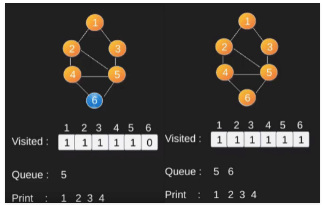
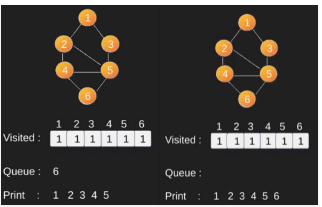
Note that the above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex (example Disconnected graph). To print all the vertices, we can modify the BFS function to do traversal starting from all nodes one by one (Like the DFS modified version).

Time Complexity: O(V + E) where V is number of vertices in the graph and E is number of edges in the graph.

Depth First Search or DFS for a Graph

Depth First Traversal (or Search) for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, a node may be visited twice. To avoid processing a node more than once, use a boolean visited array.

Example:
1. Input: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Output: DFS from vertex 1 : 1 2 0 3
Explanation:
DFS Diagram: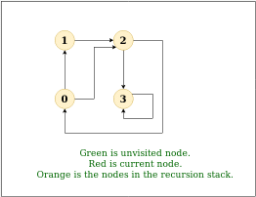

2. Input: n = 4, e = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3
Output: DFS from vertex 2 : 2 0 1 3
Explanation:
DFS Diagram: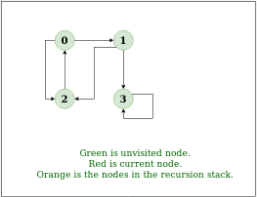

Solution

• Approach: Depth-first search is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. So the basic idea is to start from the root or any arbitrary node and mark the node and move to the adjacent unmarked node and continue this loop until there is no unmarked adjacent node. Then backtrack and check for other unmarked nodes and traverse them. Finally print the nodes in the path.
• Algorithm:
  (i) Create a recursive function that takes the index of node and a visited array.
  (ii) Mark the current node as visited and print the node.
  (iii) Traverse all the adjacent and unmarked nodes and call the recursive function with index of adjacent node.

Implementation:

• C++
  
  
• Java
  
  
  
• Python3
  
  
• C#
  
  

Output:
Following is Depth First Traversal (starting from vertex 2)
2 0 1 9 3
Complexity Analysis: 

• Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
• Space Complexity: O(V).
  Since, an extra visited array is needed of size V.

Handling Disconnected Graph 

• Solution: This will happen by handling a corner case.
  The above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex as in the case of a Disconnected graph. To do complete DFS traversal of such graphs, run DFS from all unvisited nodes after a DFS.
  The recursive function remains the same.
• Algorithm:
  (i) Create a recursive function that takes the index of node and a visited array.
  (ii) Mark the current node as visited and print the node.
  (iii) Traverse all the adjacent and unmarked nodes and call the recursive function with index of adjacent node.
  (iv) Run a loop from 0 to number of vertices and check if the node is unvisited in previous DFS then call the recursive function with current node.

Implementation:

• C++
  
  
• Java
  
  
• Python
  
  
• C#
  
  
  

Output:
Following is Depth First Traversal
0 1 2 3
Complexity Analysis

• Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
• Space Complexity :O(V).
  Since an extra visited array is needed of size V.

Applications of Depth First Search

Depth-first search (DFS) is an algorithm (or technique) for traversing a graph.
Following are the problems that use DFS as a building block.  

1. Detecting cycle in a graph
   A graph has cycle if and only if we see a back edge during DFS. So we can run DFS for the graph and check for back edges. (See this for details) 
2. Path Finding
   We can specialize the DFS algorithm to find a path between two given vertices u and z.
   (i) Call DFS(G, u) with u as the start vertex.
   (ii) Use a stack S to keep track of the path between the start vertex and the current vertex.
   (iii) As soon as destination vertex z is encountered, return the path as the contents of the stack 
3. Topological Sorting
   Topological Sorting is mainly used for scheduling jobs from the given dependencies among jobs. In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in makefiles, data serialization, and resolving symbol dependencies in linkers [2].
4. To test if a graph is bipartite 
   We can augment either BFS or DFS when we first discover a new vertex, color it opposited its parents, and for each other edge, check it doesn’t link two vertices of the same color. The first vertex in any connected component can be red or black! See this for details.
5. Finding Strongly Connected Components of a graph A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. (See this for DFS based algo for finding Strongly Connected Components)
6. Solving puzzles with only one solution, such as mazes. (DFS can be adapted to find all solutions to a maze by only including nodes on the current path in the visited set.)