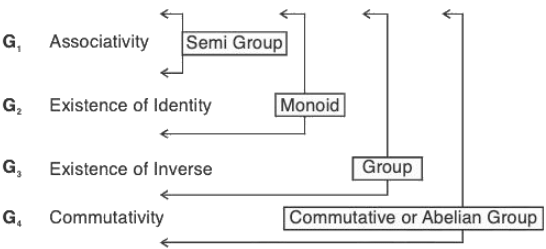
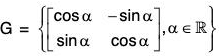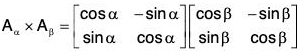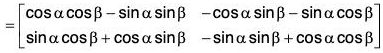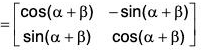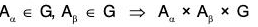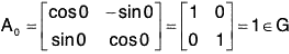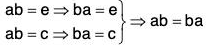Group Theory- I | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Preliminaries |

|
| Group |

|
| Abelian Group |

|
| Non-Abelian Group |

|
Preliminaries
Preliminaries
The basics of set theory : sets, ∩, U, ∈, etc. should be familiar to the reader. Our notation for subsets of a given set A will be
B = {a ∈ A I . . . (conditions on a) . . . }.
The order or cardinality of a set A will be denoted by IAl. If A is a finite set, the order of A is simply the number of elements of A.
It is important to understand how to test whether a particular x ∈ A lies in a subset B of A. The Cartesian product of two sets A and B is the collection A x B = {(a, b) | a ∈ A, b ∈ B}, of ordered pairs of elements from A and B.
We shall use the following notation for some common sets of numbers:
- 𝕫 = {0, ±1, ±2, ±3, ...} denotes the integers (the 𝕫 is for the German word for numbers: “Zahlen”).
- 𝕢 = {a/b I a, b ∈ Z and b ≠ 0} denotes the rational numbers (or rationales).
- 𝕣 = {all decimal expansions ± d1d2 ... dn.a1a2a3 ...} denotes the real numbers (or reals).
- 𝕔 = {a + bi I a, b ∈ 𝕣, i2 = -1} denotes the complex numbers.
- 𝕫+, 𝕢+ and 𝕣+ will denote the positive (nonzero) elements in Z, Q and R, respectively.
We shall use the notation f : A → B or A  B to denote a function f from A to B and the value of f at a is denoted f(a) (i.e., we shall apply all our functions on the left). We use the words function and map interchangeably. The set A is called the domain of f and B is called the codomain of f. The notation f : a → b or a → b if f is understood indicates that f(a) = b, i.e., the function is being specified on elements.
B to denote a function f from A to B and the value of f at a is denoted f(a) (i.e., we shall apply all our functions on the left). We use the words function and map interchangeably. The set A is called the domain of f and B is called the codomain of f. The notation f : a → b or a → b if f is understood indicates that f(a) = b, i.e., the function is being specified on elements.
The set f(A) = {b ∈ B I b = f(a), for some a ∈ A} is a subset of B, called the range or image of f (or the image of A under f). For each subset C of B the set f-1(C) = {a ∈ A I f(a) ∈ C} consisting of the elements of A mapping into C under f is called the preimage or inverse image of C under f. For each b ∈ B, the preimage of {b} under f is called the fiber of f over b. Note that f-1 is not in general a function and that the fibers of f generally contain many elements since there may be many elements of A mapping to the element b.
If f : A → B and g : B → C, then the composite map g of : A → C is defined by (g o f)(a) = g(f(a)).
Let f : A → B.
- f is injective or is an injection if whenever a1 ≠ a2, then f(a1) ≠ f(a2).
- f is surjective or is a surjection if for all b ∈ B there is some a ∈ A such that f(a) = b, i.e., the image of f is all of B. Note that since a function always maps onto its range (by definition) it is necessary to specify the codomain B.
- f is bijective or is a bijection if it is both injective and surjective. If such a bijection f exists from A to B, we say A and B are in bijective correspondence.
- f has a left inverse if there is a function g : B → A such that g o f : A → A is the identity map on A, i.e., (g o f)(a) = a, for all a ∈ A.
- f has right inverse if there is a function h : B → A such that f o h : B → B is the identity map on B.
Proposition : Let f : A → B.
- The map f is injective if and only if it has a left inverse.
- The map f is surjective if and only if f has a right inverse.
- The map f is a bijection if and only if there exists g : B → A such that (f o g) is the identity map on B and (g o f) is the identity map on A.
- If A and B are finite sets with the same number of elements (i.e., IAI = IBI), then f : A → B is bijective if and only if f is injective if and only if f is surjective.
A permutation (rearrangement) of a set A is simply a bijection from A to itself.
If A ⊆ B and f : B → C, we denote the restriction of f to A by flA. When the domain we are considering is understood we shall occasionally denote flA again simply as f even though these are formally different functions (their domains are different).
If A ⊆ B and g : A → C and there is a function f : B C such that flA = g, we shall say f is an extension of g to B (such a map f need not exist nor be unique).
Let A be a nonempty set.
- A binary relation on set A is a subset 𝕣 of A * A and we write a ~ b if (a, b) ∈ 𝕣.
- The relation ∼ on A is said to be :
(a) reflexive if a ~ a, for all a ∈ A,
(b) symmetric if a ~ b implies b ~ a for all a, b ∈ A,
(c) transitive if a ~ b and b ~ c implies a ~ c for all a, b, c ∈ A.
A relation is an equivalence relation if it is reflexive, symmetric and transitive. - If ~ defines an equivalence relation on A, then the equivalence class of a ∈ A is defined to be {x ∈ A I x ~ a}. Elements of the equivalence class of a are said to be equivalent to a. If C is an equivalence class, any element of C is called a representative of the class C.
- A partition of A is any collection {A( I i ∈ I} of nonempty subsets of A (I some indexing set) such that
(a) A = Ui∈I Ai, and
(b) Ai ∩ A = ∅, for all i, j ∈ I with i ≠ j
i.e., A is the disjoint union of the sets in the partition.
The notations of an equivalence relation on A and a partition of A are the same:
Proposition : Let A be a nonempty set.
- If - defines an equivalence relation on A then the set of equivalence classes of ~ form a partition of A.
- If {Ai I i ∈ I} is a partition of A then there is an equivalence relation on A whose equivalence classes are precisely the sets Ai, i ∈ I.
Properties of The Integers
The following properties of the integers Z (many familiar from elementary arithmetic)
- (Well Ordering of 𝕫) If A is any nonempty subset of 𝕫+, there is some element m ∈ A such that m ≤ a, for all a ∈ A (m is called a minimal element of A).
- If a, b ∈ 𝕫 with a ≠ 0, we say a divides b if there is an element c ∈ 𝕫 such that b = ac. In this case we write a I b; if a does not divide b we write
 .
. - If a, b ∈ 𝕫 - {0}, there is a unique positive integer d, called the greatest common divisor of a and b (or g.c.d. of a and b), satisfying:
(a) d I a and d I b (so d is a common divisor of a and b), and
(b) if e I a and e I b, then e I d (so d is the greatest such divisor).
The g.c.d. of a and b will be denoted by (a, b). If (a, b) = 1, we say that a and b are relatively prime. - The a, b ∈ 𝕫 - {0}, there is a unique positive integer l, called the least common multiple of a and b (or l.c.m. of a and b), satisfying:
(a) a | l and b | l (so l is a common multiple of a and b), and
(b) if a | m and b | m, then l | m (so l is the least such multiple).
The connection between the greatest common divisor d and the least common multiple l of two integers a and b is given dl = ab. - The Division Algorithm: if a, b ∈ 𝕫 - {0}, then there exist unique q, r ∈ 𝕫 such that a = qb + r and 0 < r < |b|,
- The Euclidean Algorithm is an important procedure which produces a greatest common divisor of two integers a and b by iterating the Division Algorithm: if a, b ∈ 𝕫 - {0}, then we obtain a sequence of quotients and remainders
a = q0b + r0 ...(0)
b = q1r0 + r1 ...(1)
ro = q2r1 + r2 ...(2)
r1 = q3r2 + r3 ...(3)
rn-2 = qnrn-1 + rn ...(n)
rn-1 = qn+1rn ...(n+1)
where rn is the last nonzero remainder. Such an rn exists since |b| > |r0| > |r1| > ... > Irnl is a decreasing sequence of strictly positive integers if the remainders are nonzero and such a sequence cannot continue indefinitely. Then rn is the g.c.d. (a, b) of a and b.
Example : Suppose a = 57970 and b = 10353. Then applying the Euclidean Algorithm we obtain:
57970 = (5)10353 + 6205
10353 = (1)6205 + 4148
6205 = (1)4148 + 2057
4148 = (2)2057 + 34
2057 = (60)34 + 17
34 = (2)17
which shows that (57970, 10353) = 17.
Modular Arithmetic
Another application of the division algorithm that will be important to us is modular arithmetic. Modular arithmetic is an abstraction of a method of counting that you often use.
If a and b are integers and n is a positive integer, we often write a = b mod n whenever n divides a - b.
(ab) mod n = ((a mod n)(b mod n)) mod n.
Similarly, (a + b) mod n = ((17 mod 10) + (23 mod 10)) and 10
Examples (7 + 3) mod 10 = 10 mod 10 = 0,
(17 • 23) and 10 = ((17 mod 10)(23 mod 10)) mod 10
(7 • 3) mod 10 = 21 mod 10 = 1.
Mathematical Induction
- First Principle of Mathematical Induction
Let S be a set of integers containing a. Suppose S has the property that whenever some integer n ≥ a belongs to S, then the integer n + 1 also belongs to S. Then, S contains every integer greater than or equal to a. - Second Principle of Mathematical Induction
Let S be a set of integers containing a. Suppose S has the property that n belongs to S whenever every integer less than n and greater than or equal to a belongs to S. Then, S contains every integer greater than or equal to a. - Definition Partition
A partition of a set S is a collection of nonempty disjoint subsets of S whose union is S. Figure illustrates a partition of a set into four subsets.
- Equivalence Classes Partition
The equivalence classes of an equivalence relation on a set S constitute a partition of S. Conversely, for any partition P of S, there is an equivalence relation on S whose equivalence classes are the elements of P.
Proof: Let the equivalence relation on A be denoted by ~ and cl(a) denotes equivalence class of a ∈ A.
We first note that since for any a ∈ A, a ~ a, a must be in cl(a), whence the union of the cl(a)’s is all of A. We now assert that given two equivalence classes they are either equal or disjoint. For, suppose that cl(a) and cl(b) are not disjoint; then there is an element x ∈ cl(a) ∩ cl(b). Since x ∈ cl (a), a ~ x; since x ∈ cl (b), b ~ x, whence by the symmetry of the relation, x ~ b. However, a - x and x ~ b by the transitivity of the relation forces a - b. Suppose, now that y ∈ cl(b); thus b ~y. However, from a ~ b and b ~y, we deduce that a ~y, that is, that y ∈ cl(a). Therefore, every element in cl(b) is in cl(a), which proves that cl(b) ⊆ cl(a). The argument is clearly symmetric, whence we conclude that cl(a) ⊆ cl(b). The two opposite containing relations imply that cl(a) = cl(b).
We have thus shown that the distinct cl(a)’s are mutually disjoint and that their union is A. This proves the first half of the theorem. Now for the other half!
Suppose that A = U Aa where the Aa are mutually disjoint, nonempty sets (a is in some index set T). How shall we use them to define an equivalence relation? The way is clear; given an element a in A it is in exactly one Aa. We define for a, b å A, a ~ b if a and b are in the same Aa. We leave it as an exercise to prove that this is an equivalence relation on A and that the distinct equivalence classes are the Aa s.
Definition
- A binary operation * on a set G is a function * : G * G → G. For any a, b ∈ G we shall write a * b for *(a, b).
- A binary operation * on a set G is associative if for all a, b, c ∈ G we have a * (b * c) = (a * b) * c.
- If * is a binary operation on a set G we say elements a and b of G commute if a * b = b * c. We say * (or G) is commutative if for all a, b ∈ G, a * b = b * a.
Examples :
- + (usual addition) is a commutative binary operation on 𝕫 (or on 𝕢, 𝕣, or 𝕔 respectively).
- x (usual multiplication) is a commutative binary operation on 𝕫 (or on 𝕢, 𝕣, or 𝕔 respectively).
- - (usual subtraction) is a noncommutative binary operation on 𝕫, where - (a, b) = a - b. The map a → -a is not a binary operation (It is unary).
- - is not a binary operation on 𝕫+ (nor 𝕢+, 𝕣+) because for a, b ∈ 𝕫+ with a < b, a - b ∉ 𝕫+, that is, - does not map 𝕫+ * 𝕫+ into 𝕫+.
- Taking the vector cross-product of two vectors in 3-space 𝕣3 is a binary operation which is not associative and not commutative.
Group
Definition :
A group is an ordered pair (G, *) where G is a set and * is a binary operation on G satisfying the following axioms:
- (a * b) * c = a * (b * c), for all a, b, c ∈ G, i.e., * is associative,
- there exists an element e in G, called an identity of G, such that for all a ∈ G we have a * e = e * a = a,
- for each a e G there is an element a-1 of G, called an inverse of a, such that a * a-1 = a-1 * a = e.
Examples
- 𝕫, 𝕢, 𝕣 and 𝕔 are groups under + with e = 0 and a-1 = -a, for all a.
- 𝕢 - {0}, R - {0}, 𝕔 - {0}, 𝕢+, 𝕣+ are groups under * with e = 1 and a-1 = 1/a, for all. Note however that 𝕫 - {0} is not a group under * because although * is an associative binary operation on 𝕫 - {0}, the element 2 (for instance) does not have an inverse in 𝕫 - {0}.
Example : The set of integers Z (so denoted because the German word for numbers is Zahlen), the set of rational numbers 𝕢 (for quotient), and the set of real numbers 𝕣 are all groups under ordinary addition. In each case, the identity is 0 and the inverse of a is -a.
Example : The set of integers under ordinary multiplication is not a group. Since the number 1 is the identity, property 3 fails. For example, there is no integer b such that 5b = 1.
Example : The subset {1,-1, i, -i} of the complex numbers is a group under complex multiplication. Note that -1 is its own inverse, whereas the inverse of i is -i, and vice versa.
Example : The set 𝕢+ of positive rationals is a group under ordinary multiplication. The inverse of any a is 1/a 5 a-1.
Example : The set S of positive irrational numbers together with 1 under multiplication satisfies the three properties given in the definition of a group but is not a group. Indeed, V√2 • V√2 = 2, so S is not closed under multiplication.
Example : A rectangular array of the form 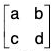 is called 2 x 2 matrix. The set o f all 2 x 2 matrices with real entries is a group under component wise addition. That is,
is called 2 x 2 matrix. The set o f all 2 x 2 matrices with real entries is a group under component wise addition. That is,
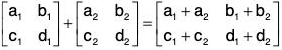
The identity is  and the inverse of
and the inverse of 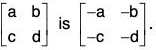
Example : The set 𝕫n = {0, 1, ..., n - 1} for n > 1 is a group under addition modulo n. For any j > 0 in 𝕫n, the inverse of j is n - j.
This group is usually referred to as the group of integers modulo n.
As we have seen, the real numbers, the 2 x 2 matrices with real entries, and the integers modulo n are all groups under the appropriate addition.
Table : Summary of Group Examples (F can be any of Q, R, C, or Zp; L is a reflection)

Elementary Properties of Groups
- Theorem : Uniqueness of the Identity
In a group G, there is only one identity element.
Proof. Suppose both e and e' are identities of G. Then,
(a) ae = a for all a in G, and
(b) e’a = a for all a in G.
The choices of a = e’ in (1) and a = e in (2) yield e’e = e’ and e’e = e. Thus, e and e’ are both equal to e’e and so they are equal to each other. - Theorem : Uniqueness of the Inverse
In a group G, there is only one inverse element.
Proof : if a1 and a2 are both inverses of a, then
a1 * (a * a2) = a1* e = a1
and (a1 * a)*a2 = e*a2 = a2
By the associative law, a1 * (a * a2) = (a1 * a) * a) * a2; hence a1 = a2. This shows that in every group, each element has exactly one inverse.
- Theorem 1 If G is a group and a, b, c are elements of G, then
(i) ab = ac implies b = c and
(ii) ba = ca implies b = c
It is easy to see why this is true: if we multiply (on the left) both sides of the equation ab = ac by a-1, we get b = c. In the case of ba = ca, we multiply on the right by a-1. This is the idea of the proof; now here is the proof :
Suppose ab = ac
Then a-1(ab) = a-1(ac)
By the associative law, (a-1a)b = (a-1a)c
that is, eb = ec
Thus, finally, b = c
Part (ii) is proved analogously.
In general, we cannot cancel a in the equation ab = ca. - Theorem 2 If G is a group and a, b are elements of G, then ab = e implies a = b1 and b = a-1
The proof is very simple: if ab = e, then ab = aa-1 so by the cancellation law, b = a-1. Analogously, a = b-1.
This theorem tells us that if the product of two elements is equal to e, these elements are inverses of each other. In particular, if a is the inverse of b, then b is the inverse of a.
The next theorem gives us important information about computing inverses. - Theorem 3 If G is a group and a, b are elements of G, then
(i) (ab)-1 = b-1a-1 and
(ii) ( a-1)-1 = a
The first formula tells us that the inverse of a product is the product of the inverses in reverse order. The next formula tells us that a is the inverse of the inverse of a. The proof of (i) is as follows:
(ab)(b-1a-1) = a[(bb-1)a-1] by the associative law
= a[ea-1] because bb-1 = e
= aa-1
= e
Since the product of ab and b ’ a 1 is equal to e, it follows by Theorem 2 that they are each other’s inverses. Thus, (ab)-1 = b-1a-1. The proof of (ii) is analogous but simpler: aa-1 = e, so by Theorem 2 a is the inverse of a-1, that is, a= (a-1)-1.
The associative law states that the two products a(bc) and (ab)c are equal; for this reason, no confusion can result if we denote either of these products by writing abc (without any parentheses), and call abc the product of these three elements in this order.
We may next define the product of any four elements a, b, c, and d in G by abed = a(bcd)
By successive uses of the associative law we find that a(bc)d = ab(cd) = (ab)(cd) = (ab)cd
Hence the product abed (without parentheses, but without changing the order of its factors) is defined without ambiguity.
In general, any two products, each involving the same factors in the same order, are equal. The net effect of the associative law is that parentheses are redundant.
Having made this observation, we may feel free to use products of several factors, such as a1a2 ... an, without parentheses, whenever it is convenient. Incidentally, by using the identity (ab)-1 = b-1a-1 repeatedly, we find that 
If G is a finite group, the number of elements in G is called the order of G. It is customary to denote the order of G by the symbol |G|.
Abelian Group
The group G is said to be abelian if a • b = b • a for all a, b ∈ G.
An abelian group is a nonempty set A with a binary operation + defined on A such that the following conditions hold:
- (Associativity) for all a, b, c ∈ A, we have a + (b + c) = (a + b) + c;
- (Commutativity) for all a, b ∈ A, we have a + b = b + a;
- ( Existence o f an additive identity there exists an element O ∈ A such that 0 + a = a for all a ∈ A;
- (Existence of additive inverses) for each a ∈ A there exists an element -a ∈ A such that -a + a = 0.

EXAMPLE OF SEMI-GROUP BUT NOT MONOID : Nonzero real numbers under the operation * defined by a*b = |a|b.
EXAMPLE OF MONOID BUT NOT GROUP : {0,1} under multiplication.
Non-Abelian Group
In mathematics, a nonabelian group, also sometimes called a noncommutative group, is a group (G, *) in which there are at least two elements a and b of G such that a * b ≠ b * a. The term nonabelian is used to distinguish from the idea of an abelian group, where all of the elements of the group commute.
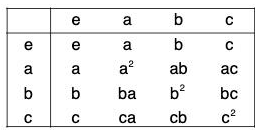
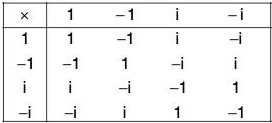
Example : Show that the set {1, - 1, i, - 1} where i = 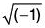 is a finite abelian group for multiplication of complex numbers.
is a finite abelian group for multiplication of complex numbers.
G = {1, -1, i -i}.
We prepare the composition table for (G, x) as follows :
On observing the table, it is clear that :
- All the entire in the table are elements of G. So multiplication of complex numbers has induced a binary composition in G.
- The number 1 is the identity element for the multiplication composition.
- The inverses of 1, - 1 , i, - i are 1, - 1 , - i and i respectively.
Since the associativity and commutativity of the multiplication of numbers is obvious, so G is a finite (of order 4) abelian group for multiplication.
Example : Show that the set {z ∈ C : |z| = 1} is a multiplicative group.
Let G = {z ∈ C : |z| = 1} and z1, z2 ∈ G; then
z1, z2 ∈ G ⇒ |z1| = 1, |z2| = 1
⇒ |z1||z2| = 1.1 = 1
⇒ |z1,z2| = 1 [∵ |z1z2| = |z1||z2|]
⇒ z1, z2 ∈ G
∴ G is closed for multiplication.
Verification of group axioms in (G, x) :
[G1] Since multiplication operation is associative in numbers, therefore this operation will also be associative in G.
[G2] ∵ |1| = 1 ⇒ 1 ∈ G, which is the identity for multiplication.
[G3] For any element z of G
z ∈ G ⇒ |z| = 1
⇒ 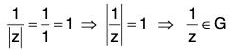
which is the multiplicative inverse of z.
Thus there exist inverse of every element in G.
Hence G is a multiplicative group.
Example : Prove that the set of n, nth roots of unity is a multiplicative finite abelian group.
Here 11/n = (1 + i0)1/n = (cos 0 + i sin 0)1/n
= (cos 2rπ + i sin 2rπ) 1/na, where r is any integer[by DeMoivre’s theorem]
= ei(2rπ)/n r = 0, 1,2, .... (n - 1)
If we take ei(2rπ)/n = θr, then the set of n complex roots
G = {1, θ, θ2, θ3, .... θn-1}
If a, b ∈ G, then an = 1 and bn = 1
Now (ab)n = an bn = 1.1 = 1
∴ ab is also the nth root of unity, therefore ab ∈ G
i.e., a, b ∈ G ⇒ ab ∈ G
Hence G is closed for multiplication.
[G1] Associativity : Complex roots are associative for multiplication.
[G2] Identity element 1 for multiplication is in G.
[G3] If any element θr, 0 ≤ r ≤ (n - 1) is in G, then there exist an element θn-r in G such that θn-r•θr = θn = i (identity) [∵ 0 is the nth root of 1]
i.e., there exist inverse θn-r of θr
[G4] Commutativity : Complex numbers are commutative for multiplication. Hence (G, x) is a finite abelian group of order n.
Example : Show that Z5 = {0, 1, 2, 3, 4} is an abelian group for the operation *+5’ defined as follows :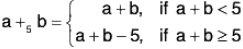
The composition table of (Z5, +5) is as follows :
From the table it is observed that
- All the elements are members of Z5 therefore ‘+5’ is a binary composition in Z5.
- 0 is the identity element for the composition.
- The inverse of 0, 1, 2, 3, 4 are 0, 4, 3, 2, and 1 respectively.
Again the base of '+5’ is the addition composition of numbers which is associative and commutative. Therefore '+3’ is also associative and commutative.
Hence (Z5,+5) is a commutative group.
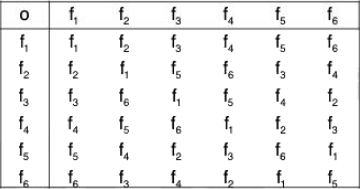
Example : Show that the set {f1, f2, f3, f4, f5, f6} is a finite non-abelian group for the operation “composite of functions” where fi, i = 1, 2,..., 6 are transformations on the infinite complex plane defined by :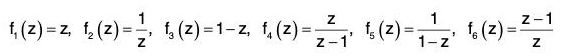
Let G = {f1, f2, f3, f4, f5, f6} and o denote composite of functions. Now calculating all the possible products under this operation, we have the following:
From these we obtain the following composition table of (G, o) :
The group axioms can be easily verified from the above composition table. There fore (G, o) is a finite group.
More over since the table is not symmetrical about the leading diagonal so it is a non commutative finite group.
Example : Show that the set Q+ of the positive relational numbers forms an abelian group for the operation * defined as :
a * b = ab/2 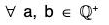
∴ * is a binary composition in Q+
Verification of group axioms in (Q+, *) :
[G1] Associativity : Let a, b ∈ Q+, then
and
∴ (a *b )*c = a *(b *c)
[G2] Existence of identity :
2 ∈ Q+ is the identity element of the operation *
because for a ∈ Q+, 2*a = a*2 = a.2/2 = a
[G3] Existence of Inverse :
For every a ∈ Q+, (4/a) ∈ Q+ (∵ a ≠ 0) which is the inverse of a
Since
So every element of Q+ is invertible.
[G4] Commutativity : For any a, b ∈ Q+[∵ multiplication is commutative]
= b*a
∴ the composition * is commutative.
Hence (Q+, *) is an abelian group.
Example : If G = {(a, b) | a, b ∈ R, a ≠ 0} and o is the operation defined in G as (a, b) o (c, d) = (ac, be + d) ; then show that (G, o) is a non-abelian group.
Verification of group axioms in (G, o) :
[G1] : Let (a, b); (c, d); (e, f) be any elements of G, then [(a, b) o (c, d)] o (e, f) = (ac, be + d) o (e, f)
= ((ac)e, (be + d)e + f)
= (ace, bee + de + f)
and (a, b) o [(c, d) o (e, f)] = (a, b) o (ce, de + f)
= (a(ce), b(ce) + de + f)
= (ace, bee + de + f)
∴ [(a, b) o (c, d)] o (e, f) = (a, b) o [(c, d) o (e, f)]
Therefore o is associative.
[G2] : Here (1, 0) ∈ G is the identity element of the operation because for every (a, b) ∈ G (1, 0) o (a, b) = (1a, 0a + b) = (a, b)
and (a, b) o (1, 0) = (a1, b1 + 0) = (a, b)
[G3] : If (a, b) ∈ G, then a ≠ 0
∴
Again
and
∴is the inverse of (a, b)
Thus the inverse of every element of G also exist in G.
Hence (G, o) is a group.
[G4] : The composition of the group is not commutative because if a, b, c, d are different real numbers, then (a, b) o (c, d) = (ac, bc + d)
≡ (ca, da + b) = (c, d) o (a, d)
⇒ (a, b) o (c, d) ≠ (c, d) o (a, b)
As such (G, o) is a non abelian group.
Example : Show that G = 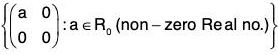 is a commutative group under matrix multiplication.
is a commutative group under matrix multiplication.
Let
be any two elements of G, where a, b ∈ R0; then AB =
∵ a ∈ R0, b ∈ R0 ⇒ ab ∈ R0
∴ AB = G which shows that G is closed for matrix multiplication.
Verification of group axioms in (G, x) :
[G1] : Since Matrix multiplication is associative.
Therefore this is associative in G also.
[G2] : E =is the identity element because
[G3] : For every(∵ a ∈ R0 ⇒ 1/a ∈ R0)
which is inverse of A because(Identity)
[G4] : Since AB =and ab = ba (by commutativity of multiplication of real numbers),
Therefore, AB = BA
As such matrix multiplication is commutative in G.
Hence G is a commutative group for matrix multiplication.
Example : Show that the set of all the matrices of the form  is an abelian group for matrix multiplication.
is an abelian group for matrix multiplication.
Let
and Aα, Aβ, ∈ G, where α, β ∈ R, then,
= Aα+β ∈ G [∵ α + β ∈ R]
∴
Consequently G is closed for matrix multiplication.
Verification of group axioms in (G, x) :
[G1] : Matrix multiplication is associative.
Therefore, this is associative in G also.
[G2]: For α = 0
which is the identity for matrix multiplication.
[G3]: For every Aα ∈ G, A(-α), ∈ G which is the inverse of Aα, because Aα x A(-α) = Aα-α = A0 and A(-α) x Aα = A(-α + α) = A0
Therefore, the inverse of every element of G exists in G.
[G4]: For any two elements Aα and Aβ of G
Aα x Aβ = Aα+β [proved above]
= Aβ+α [∵ α, β ∈ R ⇒ α + β = β + α]
Therefore, matrix multiplication is commutative in G.
As such G is a commutative group for matrix multiplication.
Example : The set G = {1, 2, 3, 4...(p - 1)}, xp. p being prime is an abelian group of order (p - 1) with respect to multiplication modulo p.
Let a, b ∈ G, then 1 ≤ a ≤ (p - 1), 1 ≤ b ≤ (p - 1)
By definition, a xP b = r, where r is the least non negative remainder when ordinary product is divided by p.
Now since p is prime, therefore ab is not divisible by p
Consequently, r ≠ 0, 1 ≤ r ≤ (p - 1)
therefore a xp b ∈ G ∀ a, b ∈ G
⇒ G is closed for the multiplication modulo p.
[G1] : Associativity : Let a, b, c ∈ G then
a xp (b xp c) = a xp (bc) [∵ b xp c = be (mod p)]
= the least non-negative remainder obtained on dividing a(bc) by p
= the least non-negative remainder obtained on dividing (ab)c by p
= (ab) xp c = (a xp b) xp c [∵ ab = a xp b(mod p)]
Therefore multiplication modulo p is associative.
[G2] : 1 ∈ G is the identity element because for every a ∈ G
1 xp a = a xp 1 = a
[G3] : Let s ∈ G then 1 ≤ s ≤ (p - 1).
Consider the following (p - 1) products :
1 xp s, 2 xp s, 3 xp s, ... (p - 1) xp s
All these are elements of G and no two of these are equal since if 1 ≤ i ≤ (p - 1), 1 ≤ j ≤ (p - 1) and i > j, then i xp s = j xp s
⇒ (i s) and (j s) leave the same non-negative remainders when divided by p
⇒ (i s - j s) is divisible by p
⇒ (i - j)s is divisible by p
But this is not possible because
1 ≤ (i - j) ≤ (p - 1), 1 ≤ s ≤ (p - 1) and p is prime.
∴ i xp s ≠ j xp s
and (p - 1) distinct elements of G and so one of the products must be equal to 1.
Let r xp s = 1 ⇒ is the inverse of s
Therefore every element of G is invertible.
and (p - 1) distinct elements of G and so one of the products must be equal to 1.
Let r xp s = 1 ⇒ r is the inverse of s
Therefore, every element of G is invertible.
[G4] : a xp b = the least non-negative remainder obtained on dividing ab by p
= the least non-negative remainder obtained on dividing (ba) by p
= b xp a (∵ ba = ab)
Therefore, multiplication modulo p is commutative.
Hence G is an abelian group of order (p - 1).
Remark. If p is not prime, then G will not be a group because G will not be closed for multiplication.
Example : The set of residue classes modulo m is an abelian group with respect to the addition of residue classes.
Let I = { . . . , -3 , -2 , -1 , 0 , 1, 2, 3, ...} be the set of integers. If a ∈ I, then [a] is a residue class modulo m of I if [a] = {x : x ∈ I and x - a is divisible by m}.
Let Im be the set of all residue class of I mod m
i.e., Im = {[a] : a ∈ I}. We have [a] = [b] ⇔ a = b (mod m). The set lm has m distinct elements [0], [1], [2]......[m - 1]. Thus we have
lm = {[0], [1], [2], .... [m - 1]}.
Let a and b are any two integers, then we define the addition of residue classes [a] and [b] as follows :
[a] + [b] = [a + b].
If [a] = [c] and [b] = [d], then it can be easily seen that [a] + [b] = [c] + [d].
Therefore, our addition of residue classes is well-defined.
Now we shall show that lm is a group with respect to addition of residue classes.
Closure Property :
If [a], [b] ∈ lm, then by definition [a] + [b] = [a + b]. Since a + b is an integer, therefore [a + b] ∈ lm. Thus lm is closed with respect to addition of residue classes.
Associativity : Let [a], [b], [c] be any three elements of lm. Then [a] + ([b] + [c]).
= [a] + [b + c] [by def. of addition of residue classes]
= [a + (b + c)] [by def. of addition of residue classes]
= [(a + b) + c] [∵ addition of integers is a associativity]
= [a + b] + [c] = ([a] + ([b] + [c].
Commutativity : Let [a], [b] ∈ lm. Then [a] + [b] = [a + b] = [b + a] = [b] + [a].
Existence of Identity : We have [0] ∈ Im. If [a] ∈ lm, then we have [0] + [a] = [0 + a] = [a] = [a] + [0]. Therefore, the residue class [0] is the identity element.
Existence of Inverse : We have [0] ∈ lm. If [a] ∈ lm, then we have [0] + [a] = [0 + a] = [0 + a] = [a] + [0]. Therefore, the residue class [0] is the identity element.
Existence of Inverse : Let [a] ∈ lm be arbitrary. Since a ∈ I - a ∈ I, therefore [-a] is also an element of lm. We have [-a] + [a] = [-a + a] = [0] = [a] + [-a]. Thus, [-a] is the inverse of [a].
Thus lm is an abelian group with respect to addition of residue classes.
Since the number of distinct elements in lm is m, therefore the order of this group is m,
Note : If [r] = lm and 0 ≤ r < m, then the inverse of [r] is [m - r]. We have [r] + [m - r] = [r + (m - r)] = [m] = [0].
Note that m I m ⇒ [m] = [0].
Elementary Properties of Groups
1. Uniqueness of the Identity
In a group G, there is only one identity element.
Proof. Suppose both e and e’ are identities of G. Then,
1. ae = a for all a in G, and
2. e’a = a for all a in G.
The choice of a = e’ in (1) and a = e in (2) yields e’ e = e’ and e’ e = e. Thus, e and e’ are both equal to e’ e and so are equal to each other.
Theorem : (Uniqueness of inverse)
The inverse of an element in a group is unique.
Proof. Let a be any element of the group (G, *) which has two inverses b and c in the group.
a-1 = b ⇒ ba = e = ab
and a-1 = c ⇒ ca = e = ac
Now ba = e ⇒ (ba) c = ec
⇒ b(ac) = c [by G1 and G2]
⇒ be = c [by (2)]
⇒ b = c [by G3]
Therefore, the inverse of every element of a group is unique.
Remark. The inverse of the identity of a group is itself.
Theorem : If G is a group then for a, b ∈ G:
(a) (a-1)-1 = a (b) (ab)-1 = b-1 a-1
i.e. the inverse of the produced of two elements is the product of their inverses in the reverse order.
Proof, (a) Since a-1 is the inverse of a, therefore aa-1 = e = a-1 a
⇒ a-1 a = e = aa-1
⇒ inverse of a-1 = a, i.e. (a-1)-1 = a.
Remark. For the additive operation - (-a) = a.
(b) Since a, b, a-1, b-1, ab, b-1 a-1 all are element of G, therefore
(ab)(b-1a-1) = a(bb-1)a-1 [by G1]
= aea-1 [by G3]
= aa-1 [by G2]
= e
∴ (ab)(b-1a-1) = e ...(1)
Again (b-1a-1)(ab) = b-1(a-1 a)b
= b-1eb [by G1]
= b-1b [by G3]
= e [by G2]
∴ (b-1a-1)(ab) = e ...(2)
From (1) and (2),
(ab)(b-1a-1) = e = (b-1a-1)(ab)
⇒ (ab)-1 = b-1 a-1
Generalised reversal law :
By principle of induction, the above theorem can be generalised as :
(a1a2a3...an)-1 =
Remark : If the composition is addition (+) then this can be written as :
-(a + b) = (-b) + (-a)
Remark : If G is a commutative group, then for a, b ∈ G
(ab)-1 = a-1 b-1
Theorem : Cancellation law :
If a, b, c are elements of a group G, then :
(a) ab = ac ⇒ b = c
(b) ba = ca ⇒ b = c
Proof. ∵ a ∈ G ⇒ a-1 ∈ G [by G3]
∴ ab = ac ⇒ a-1 (ab) = a-1 (ac)
⇒ (a-1 a)b = (a-1 a)c [by G1]
⇒ eb = ec [by G3]
⇒ b = c [by G2]
Similarly, it can be proved that ba = ca ⇒ b = c
Theorem : If a, b are elements of a group G, then the equations ax = b and ya = b have unique solutions in G.
Proof. ∵ a ∈ G ⇒ a-1 ∈ G [by G3]
∴ a ∈ G, b ∈ G ⇒ a-1b ∈ G
Now a(a-1 b) = (aa-1)b [by G1]
= eb [by G3]
= b
Therefore, x = a-1 b is a solution of the equation ax = b in G.
Uniqueness : Let the equation ax = b have two solutions x = x1 and x = x2 in G, then ax1 = b and ax2 = b
⇒ ax1 = ax2
⇒ x1 = x2 [by left cancellation law]
Therefore, the solution of ax = b is unique in G.
Similarly, its can also be proved that the solution of the equation ya = b is unique in G.
Theorem : Alternate definition of a group :
If for all elements a, b of a semigroup G, equations ax = b and ya = b have unique solutions in G, then G is a group.
Proof. G being semi group, is a non empty set. Therefore let a ∈ G, then the equations ax = a and ya = a will have unique solutions in G. Let these solutions be denoted by e1 and e2 respectively, then
ae1 = a and e2a = a ...(i)
Again if b be any other element of g, then by the given property
x, y ∈ G so that ax = b and ya = b ...(ii)
Now ya = b ⇒ (ya)e1 = be1
⇒ y(ae1) = be1 [by associativity in G]
⇒ ya = be1 [by (i)]
⇒ b = be1 [by (ii)]
∴ e1 is the right identity in G.
Again ax = b ⇒ e2(ax) = e2b
⇒ (e2a)x = e2b [by associativity in G]
⇒ ax = e2b [by (i)]
⇒ b = e2b [by (ii)]
∴ e2 is the left identity in G.
Since e1 is right identity in G and e2 is in G ⇒ e2e1 = e2
Also e2 is left identity in G and e1 is in G ⇒ e2e1 = e1 ⇒ e1 = e1
Hence there exists an identity e1 = e2 = e (say) in G.
Again using the given property for the elements a, e e G we find that the equations ax = e and ya = e have unique solutions in G.
Let these solutions be xa and ya respectively. So
axa = e and yaa = e ...(iii)
⇒ xa and ya are right and left inverses of a in G.
Now axa = e ⇒ ya(axa) = yae
⇒ (yaa)xa = ya [by associativity in G]
⇒ exa = ya [by (iii)]
⇒ xa = ya
∴ there exist the inverse of a in G.
Since the identity exist and every element of G is invertible in the semigroup G, therefore G is a group.
Remark. If G is a semi group such that for a, b in G, only the equation ax = b (or ya = b) has a unique solution in G, then G may not be a group.
This can be observed by the following example :
Example : Let G be any non-empty set having at-least two elements.
Define a binary operation (*) in G as follows :
a*b = b ∀ a, b ∈ G
∵ For a, b, c ∈ G (a*b)*c = b*c = c
and a*(b*c) = a*c = c
∴ (a*b)*c = a*(b*c)
Therefore the composition * of G is associative.
Hence (G, *) is a semi group.
Again we see that a * b = b ⇒ x = b i s a solution of ax = b in G.
But trivially (G, *) is not a group as there is a no right identity in G.
Theorem : If G is finite semigroup such that for any a, b, c ∈ G
(a) ab = ac ⇒ b = c
and (b) ba = ca ⇒ b = c
then G is a group.
Proof. Since G is a non void finite set, so let
G = {a1, a2, a3......an}
If a ∈ G, then the n products aa1, aa2, ..., aan ...(1)
are all elements of G (∵ G is a semi group)
Again all these are distinct elements because
if aai = aaj, then by the given property
aai, = aaj ⇒ ai = aj
So all elements of (1) are n distinct elements of G, placed possibly in a different order i.e. G = {aa1, aa2......aan}
Now if b ∈ G, then b is one of the above n products.
Therefore, let aar = b, ar ∈ G
Hence we see that for any a, b ∈ G, the equation ax = b has a unique solution in G.
Similarly by considering the n products a1a,a2a....ana it can be shown that for every pair a, b ∈ G, the equation ya = h has a unique solution in G. Hence by theorem G is a group.
Remark : If G is an infinite semi group satisfying cancellation law but it is not a group.
Example : The positive integers under multiplication form a cancellative semigroup, but is not a group.
Theorem : Definition of a group based on left axioms.
A finite semigroup G is a group iff :
(i) there exists e ∈ G such that ea = a, ∀ a ∈ G (Left Identity)
(ii) there exists b ∈ G such that ba = e, ∀ a ∈ G (Left Inverse)
Proof. If G is a group, then by the definition of a group the above properties (i) and (ii) must obviously hold true.
Conversely, if a semi group G satisfies both the properties (i) and (ii), then we have to prove that G is a group. For this we have to show that e is the identity in G and b is the inverse of a i.e.
ea = a = ae, ∀ a ∈ G
and ba = e = ab
Let a ∈ G, then by the given property (ii), there exists an element b such that
ba = e ...(1)
Again by the same property there exists c such that
cb = e ...(2)
Now for a, b ∈ G ab = e(ab) [by property (i)]
= (cb)(ab) [by (2)]
= c(ba)b [by associativity in G]
= (ce)b [by property (ii)]
= c(eb)
= cb [by property (i)]
= e [by (2)]
∴ ba = e = ab which prove that b is the inverse of a.
Further, we see that ae = a(ba) [∵ e = ab]
= (ab)a [by associativity in G]
= ea [∵ ab = e]
= a [by property (i)]
∵ ea = a = ea which proves that e is the identity in G.
Therefore, G is a group.
Theorem : Definition of a group based on right axioms :
A semigroup G is group iff :
(i) ∃ e ∈ G such that ae = a, ∀ a ∈ G
(ii) ∃ b ∈ G such that ab = e, ∀ a ∈ G
This can be proved similar to the previous theorem.
Caution : It should be noted that a semi group G may be such that G contains a left identity e and each element a in G has a right inverse related to e. In such a case G may fail to be a group. This will be clear by the following example :
Example : Let G be a set containing atleast two elements.
Define a composition (•) in G as follows :
a • b = b, ∀ a, b ∈ G
Obviously G is a semi group. Let e be any fixed element of G. Then by definition, for every a ∈ G, ea = a. So e is a identity of a.
Also for each a ∈ G, ae = e ⇒ e is a right inverse of a wrt e.
But G is not a group as G does not have any right identity.
Finite and Infinite group
A group (G, *) is said to be finite if its underlying set G is a finite set and a group which is not finite is called an infinite group.
Order of a Group
The number of elements of a group (finite or infinite) is called its order. We will use IGI to denote the order of G.
Thus, the group Z of integers under addition has infinite order, whereas the group U(10) ={1, 3, 7, 9} under multiplication modulo 10 has order 4.
Integral powers of an element in a group
Let (G, *) be a group and a ∈ G, then a*a, a*a*a, a*a*a, are all elements of G and shall be written as a2, a3, a4 respectively.
Thus (a) for any positive integer n,
an = a*a*a*...*a (n times)
(b) If n is a negative integer : Let n = -n where m is a positive integer, then a" can be defined as follows :
an = a-m = (a-1)m = a-1 * a-1 *...* a-1 (m times)
Therefore a-2 = a-1 * a-1, a-3 = a-1 * a-1 * a-1 etc.
More over we define a0 = e, ∀ a ∈ G where e is the identity in G.
Law of indices : If a ∈ G and m, n are integers, then by mathematical induction, the following laws can be easily established :
(a) am + n = am an (b) (am)n = an m
Note. When the composition of a group is addition (+), then an is written as n and in that case if m and n are positive integers, then na = a + a + ... + a (n times)
(-m)a = (-a) +...+ (-a) (m times)
(m + n)a = ma + na
and n(ma) = (nm)a
Order of an Element
The order of an element g in a group G is the smallest positive integer n such that gn = e. (In additive notation, this would be ng = 0). If no such integer exists, we say g has infinite order. The order of an element g is denoted by Igl.
So, to find the order of a group element g, we need only compute the sequence of products g, g2, g3,..., until you reach the identity for the first time. The exponent of this product (or coefficient if the operation is addition) is the order of g. If the identity never appears in the sequence, then g has infinite order.
Remark. From the above definition, it is clear that for any element a of a group if an = e then 0(a) ≤ n.
Example : In the group (Z,+), the order of 0 is 1 and the order of every non zero integer a is infinite, because for any a ∈ Z(a ≠ 0) there exists no positive integer n such that na = 0.
Example : In the group (Q0, *), O(1) = 1, O(-1) = 2 and order of all the remaining elements is infinite.
Example : In the multiplicative group {1, ω, ω2} (ω3 = 1)
0(1) = 1, O((ω) = 3, 0(ω2) = 3.
Example : In the multiplicative group { 1 , - 1 , i, - i } since 11 = 1, (-1)2 = 1, i4 = 1, and (-i)4 = 1 so O(1) = 1, O(-1) = 2, O(i) = 4 and O(-i) = 4.
Example : In the group [{0, 1, 2, 3}, +4]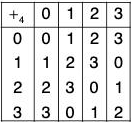
Here 0 is the identity element
0 +4 0 = 0 ⇒ O(0) = 1
1 +4 0 = 1, 1 +4 1 = 2, 1 +4 2 = 3, 1 +4 3 = 0 → O(1) = 4
2 +4 0 = 2, 2 +4 1 = 3, 2 +4 2 = 0 ⇒ O(2) = 3
3 +4 0 = 3, 3 +4 1 = 0 ⇒ O(3) = 2
Example : In Klein’s 4 group every element except identity is of order 2.
Properties of the order of an element of a group
Theorem : The order of the identity of every group is 1 and it is the only element of order 1.
Proof. Let e be the identity of any group G.
∵ e1 = e, ∴ O(e) = 1
Again if a ∈ G and O(a) = 1, then
O(a) = 1 ⇒ a1 = e ⇒ a = e
Therefore O(a) = 1 ⇒ a = e
Theorem : The order of every element of a finite group is finite and less than or equal to the order of the group i.e.,
O(a) ≤ O(G), ∀ a ∈ G
Proof. Let G be a finite group of order n and a ∈ G.
We see that a0, a1, a2, .... an are all elements of G But G contains n elements and the number of these elements is (n + 1), so all can not be distinct. Therefore atleast two of these elements are equal.
Let ai = ai, 0 ≤ j ≤ i ≤ n
⇒ aia-j = aj a-j
⇒ ai-j = a0 = e
⇒ ar = e, where 0 < r = i - j ≤ n
⇒ O(a) ≤ r ≤ n = O(G)
Hence O(a) is also finite and less than or equal to O(G).
Remark : The above theorem can also be stated as follows :
If G is a finite group of order n, then for any a ∈ G, there exists a positive integer r ≤ n such that ar = e.
Theorem : If order of an element a of a group (G, *) is n, then am = e, iff m is a multiple of n.
Proof. First of all, suppose that am = e
Now since m and n are integers, so by division algorithm in integer, there exist integers q and r such that
m = nq + r, 0 ≤ r < n
∴ am = e ⇒ anq+r = e ⇒ anq ar = e
⇒ (an)q ar = e [∵ (am)n = amn]
⇒ eq-ar = e [∵ O(a) = n ⇒ an = e]
⇒ ar = e ⇒ r = 0 [∵ 0 ≤ r < n]
⇒ m = nq i.e., m is a multiple of n.
Conversely : Let m be a multiple of n i.e. m = nq(q 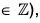 then m = nq ⇒ am = anq = (an)q = eq = e
then m = nq ⇒ am = anq = (an)q = eq = e
Therefore, am = e ⇔ m is a multiple of O(a).
Cor. : The order of any integral power of an element a of a group (G,*) can not exceed the order of the element.
Proof. Let a be any element of a group G and O(a) = n.
Then for any k ∈ 
(ak)n = ank = (an)k = ek = e
⇒ O(ak) ≤ n ⇒ O(ak) ≤ O(a)
Cor. : The order of an element a of a group (G, *) is equal to that of its inverse a-1 i.e., O(a) = O(a-1).
Proof. Let O(a) = n and O(a-1) = m
Now a-1 is an integral power of a ⇒ 0(a-1) ≤ O(a)
⇒ m ≤ n ...(1)
Again a = (a-1) ⇒ a is the integral power of a-1
⇒ O(a) ≤ O(a-1)
⇒ n ≤ m ...(2)
(1) and (2) ⇒ m = n, i.e. O(a-1) = O(a)
Cor. : If any element of a group G is of order n, then order of ak is n/m where m is g.c.d. of n and k.
You have two things to show. Namely that:
- (ak)n/gcd(n.k) = e(where e denotes the identity)
and that n/gcd(n, k) is the smallest positive power p of ak such that (ak)p = e: - For all m > 0: (ak)m = e ⇒ n/gcd(n, k) ≤ m
The first part is easy:
(ak)n/gcd(n,k) = (an)k/gcd(n,k) = ek/gcd(n,k) = e
For the second part, let 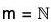 be such that (ak)m = akm = e. Since the order of a is n, it follows that n I km. Therefore we also have
be such that (ak)m = akm = e. Since the order of a is n, it follows that n I km. Therefore we also have 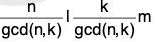
Now gcd(n/gcd(n, k), k/gcd(n, k)) = 1 (try to prove this), so it follows that n/gcd(n, k) I m
Hence in particular n/gcd(n, k) ≤ m.
Theorem : For any element a of a group G :
O(a) = O(x-1 ax), ∀ x ∈ G
Proof. Let a ∈ G, x ∈ G, then
(x-1 ax)2 = (x-1 ax)(x-1 ax)
= x-1 (xx-1)ax [by associativity]
= x-1 aeax = x-1 (aea)x
= x-1 a2x
Again let (x-1ax)n-1 = x-1 an-1 x , where(n - 1) 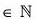
⇒ (x-1 ax)n-1 (x-1 ax) = (x-1 an-1x) (x-1 ax)
⇒ (x-1 ax)n = x-1an-1 (xx-1)ax = x-1an-1 (eax)
= x-1an-1ax = x-1 anx
Therefore, by induction method,
(x-1 ax)n = x-1 an x, 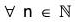
Now let O(a) = n and O(x-1 ax) = m, then (x-1 ax)n = x-1anx = x-1 ex = e
⇒ 0(x-1 ax) ≤ n ⇒ m ≤ n ...(1)
Again 0(x-1 ax) = m ⇒ (x-1ax)m = e ⇒ x-1 am x = e
⇒ x(x-1 amx)x-1 = xex-1 = e
⇒ (xx-1) am(xx-1) = e
⇒ eam e = e ⇒ am = e
⇒ O(a) ≤ m ⇒ n ≤ m ...(2)
(1) and (2)
⇒ n = m ⇒ O(a) = O(x-1 ax)
If O(a) is infinite, then 0(x-1 ax) will also be infinite.
Cor. : If a and b are elements of a group G; then O(ab) = O(ba)
Let n and m be the order of ab and ba, respectively. That is, (ab)n = e, (ba)m = e,
where e is the identity element of G.
We compute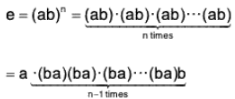
= a(ba)n-1 b.
From this, we obtain(ba)n-1 = a-1 b-1 = (ba)-1, and thus we have (ba)n = e.
Therefore the order m of ba divides n.
Similarly, we see that n divides m, and hence m = n.
Thus the orders of ab and ba are the same.
Proof. ∵ b-1 (ba)b = (b-1b)(ab) [by associativity]
= e(ab) = ab
Therefore by the above theorem, O(ba) = O(b-1(ba) b) = O(ab)
Theorem : If the order of an element a of a group G is n, then the order of ap is also n provided p and n are relatively prime.
Proof. Let O(ap) = m
∵ O(a) = n ⇒ an = e ⇒ anp = eP = e
⇒ (ap)n = e ⇒ O(ap) ≤ n
⇒ m ≤ n ...(1)
Again since p and n are relatively prime, therefore GCD of p and n = 1
⇒ there exist two integers x and y such that px + ny = 1
⇒ a1 = apx+ny = apx • any
= apx .(an)y = apx.ey
= apx .e = apx
am = (apx)m = ampx = (amp)x = ex = e
⇒ O(a) ≤ m
⇒ n ≤ m ...(2)
(1) and (2) ⇒ n ≤ m ⇒ O(a) = O(ap)
Example : If for every element a of a group G, a2 = e; then prove that G is abelian.
Let a, b ∈ G, then by the given property
a ∈ G ⇒ a2 = e ⇒ aa = e
⇒ a-1 = a ...(1)
Similarly b ∈ G ⇒ b-1 = b ...(2)
Now a ∈ G, b ∈ G ⇒ ab ∈ G
⇒ (ab)-1 = ab [by the given property]
⇒ b-1a-1 = ab [by reversal law]
⇒ ba = ab [by (1) and (2)]
∴ G is an abelian group.
Example : If a, b are any two elements of a group G; then show that G is an abelian group if (ab)2 = a2 b2.
Let G be an abelian group, then G is abelian ⇒ ab = ba, ∀ a, b ∈ G
⇒ (ab)(ab) = (ba)(ab)
⇒ (ab)2 = b(aa)b [by associativity]
⇒ (ab)2 = (ba2)b
⇒ (ab)2 = (a2b)b [∵ G is abelian]
⇒ (ab)2 = a2(bb)
⇒ (ab)2 = a2 b2Conversely : For a, b ∈ G, (ab)2 = a2 b2, then (ab)2 = a2 b2 ⇒ (ab) (ab) = (aa) (bb)
⇒ a(ba)b = a(ab)b [by associativity]
⇒ G is an abelian group.
Therefore G is an abelian group ⇔ (ab)2 = a2 b2.
Example : If a is an element of a group G, then show that : a2 = a ⇔ a = e
Let a ∈ G and a2 = a then a2 = a ⇒ aa = ae
⇒ a = e [by left cancellation law]
Conversely : If a = e, then
a = e ⇒ aa = ea
⇒ a2 = a
Therefore a2 = a ⇔ a = e
Remark. For any element a of a group G, if a2 = a, then a is called an idempotent.
The identity element of the given group is 1, therefore O(a) = 1. For other elements, we see that
22 = 4, 23 = 3, 24 = 1 ⇒ O(2) = 4.
32 = 4, 33 = 2, 34 = 1 ⇒ O(3) = 4.
and 42 = 2 ⇒ O(4) = 2.
Example : If a, b are two elements of a group G such that am bn = ba, ∀ m, n 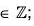 ; then prove that : ambn-2, am-2bn, ab-1 are element of the same order in G.
; then prove that : ambn-2, am-2bn, ab-1 are element of the same order in G.
ambm-2 = ambnb-2 = (ambn)b-2 = (ba)b-2
= (ba)(b-1b-1) [∵ ambn = ba]
= b(ab-1)b-1 = (b-1)-1 (ab-1) (b-1)
∴ O(ambn-2) = O(ab-1) [∴ O(a) = O(x-1 ax), ∀ x ∈ G] ...(1)
Again am-2bn = a-2 (ambn) = a-1a-1 ba [∵ ambn = ba]
am-2bn = a-1(a-1b)a
∴ O(am-2 bn) = O(a-1(a-1b)a)
= O(a-1b) [∵ O(a) = 0(x-1 ax), ∀ x ∈ G]
= O(a-1 b)-1 [∵ O(x) = 0(x-1)]
= O(b-1a) = O(eb-1 a)
= O(a-1 ab-1 a)
= O( a-1 (ab-1)a) = O(ab-1) ...(2)
From (1) and (2),
O(ambn-2) = O(am-2bn) = O(ab)-1
Example : If a is the only element of order 2 in a group G, then show that ax = xa, ∀ x ∈ G.
We know that for any element a in a group G.
O(a) = O(x-1 ax), ∀ x ∈ G
∴ O(a) = 2 ⇒ O(x-1 ax) = 2
But a is the only element of order 2 in G, therefore
O(a) = O(x-1 ax) ⇒ a = x-1 ax
⇒ xa = x(x-1 ax)
⇒ xa = ax, ∀ x ∈ G
Example : If G is a group such that (ab)m = ambn for three consecutive integers m, m + 1, m + 2 for all a, b ∈ G; show that G is abelian.
a, b ∈ G, then as given
(ab)m = ambm ...(i)
(ab)m+1 = am+1 bm+1 ...(ii)
(ab)m+2 = am+2 bm+2 ...(iii)
Now (ab)m+2 = (ab)m+1 ab
⇒ am+2 bm+2 = am+1 bm+1 ab [by (ii) and (iii)]
⇒ am+1 abm+1 b = bm+1 bm+1 ab
⇒ abm+1 = bm+1 a [by cancellation law]
⇒ am(abm+1) = am(bm+1 a)
⇒ (ama)bm+1 = am(bmb)a
⇒ am+1bm+1 = ambm(ba)
⇒ (ab)m+1 = (ab)m (ba)
⇒ (ab)m (ab) = (ba)m (ba)
⇒ ab = ba
∴ G is an abelian group.
Example : If a, b are elements of an abelian group G, then prove that :
(ab)n = anbn, 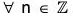
Case (i) When n = 0, then (ab)° = e = ee [by definition]
= a° b°
Case (ii) when n > 0; If n > 1, then (ab)1 = ab = a1 b1
∴ The result is true for n = 1.
Let the result be true for n = k, then (ab)k = ak bk
⇒ (ab)(ab)k = (ab)(ak bk)
⇒ (ab)k+1 = a(bak)bk [by associativity]
⇒ = a(akb)bk [by commutativity in G]
⇒ = (aak)(bbk) = ak+1 bk+1
Thus if the result is true for n = k, it is also true for n = k + 1.
Hence by principle of induction it is true for all integers.
Case (iii) When n < 0, then let n = - m , where m ∈ Z+, then
(ab)n = (ab)-m = [(ab)m]-1
= (ambm)-1 [by case (ii)]
= (bm am)-1 [by commutativity in G]
= (am)-1 (bm)-1 = a-m b-m
= an bn
Combining all the three cases, we conclude that G is commutative ⇒ (ab)n = anbn, ∀
Example : Prove that every group of order 4 is an abelian group.
Let G = {e, a, b, c} be a group of order 4 with e as its identity. Its composition table is as under :
Since every element of the group appears only once in each row of the composition table, therefore in the second row
ab = e or ab = b or ab = c
But ab = b ⇒ a = e which is not possible (∵ a ≠ e)
∴ ab ≠ b, Hence ab = e or, ab = c
Similarly in the third row ba ≠ a
∴ ba = e or ba = c
Since every element of the group appears only once in each column of the composition table, therefore
and
Similarly it can be seen that
ac = ca and be = cb
Hence G is an abelian group.
Example : Consider 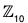 under addition modulo 10. Since 1-2 = 2, 2-2 = 4, 3-2 = 6, 4-2 = 8, 5-2 = 0, we know that |2| = 5. Similar computations show that |0| = 1, |7| = 10, |5| = 2, |6| = 5.
under addition modulo 10. Since 1-2 = 2, 2-2 = 4, 3-2 = 6, 4-2 = 8, 5-2 = 0, we know that |2| = 5. Similar computations show that |0| = 1, |7| = 10, |5| = 2, |6| = 5.
|
98 videos|27 docs|30 tests
|
FAQs on Group Theory- I - Mathematics for Competitive Exams
| 1. What is group theory? |  |
| 2. What is an abelian group? |  |
| 3. What is the difference between an abelian group and a non-abelian group? |  |
| 4. What are some examples of abelian groups? |  |
| 5. What are some examples of non-abelian groups? |  |

|
Explore Courses for Mathematics exam
|

|
 .
.

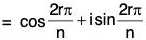 [by DeMoivre’s theorem]
[by DeMoivre’s theorem]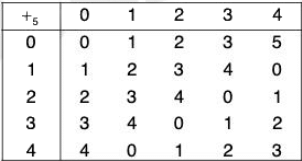
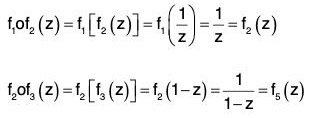
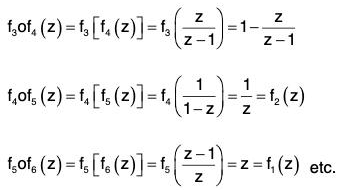
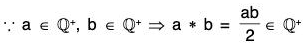
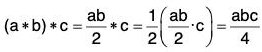
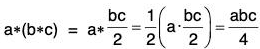
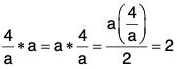
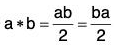 [∵ multiplication is commutative]
[∵ multiplication is commutative]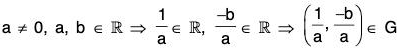
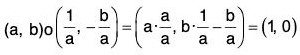
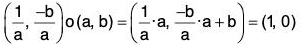
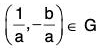 is the inverse of (a, b)
is the inverse of (a, b)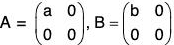 be any two elements of G, where a, b ∈ R0; then AB =
be any two elements of G, where a, b ∈ R0; then AB = 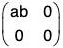 ∵ a ∈ R0, b ∈ R0 ⇒ ab ∈ R0
∵ a ∈ R0, b ∈ R0 ⇒ ab ∈ R0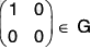 is the identity element because
is the identity element because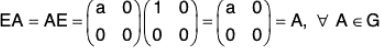
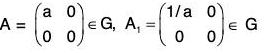 (∵ a ∈ R0 ⇒ 1/a ∈ R0)
(∵ a ∈ R0 ⇒ 1/a ∈ R0)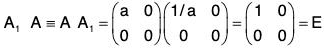 (Identity)
(Identity)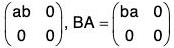 and ab = ba (by commutativity of multiplication of real numbers),
and ab = ba (by commutativity of multiplication of real numbers),