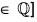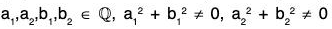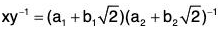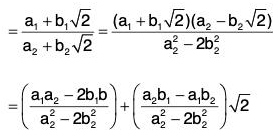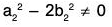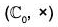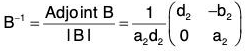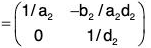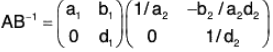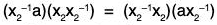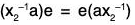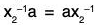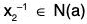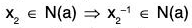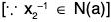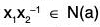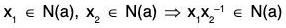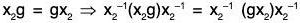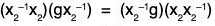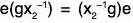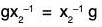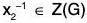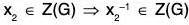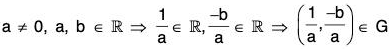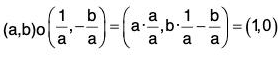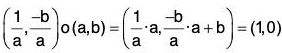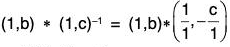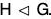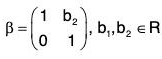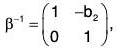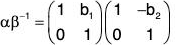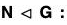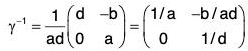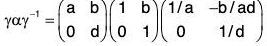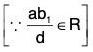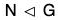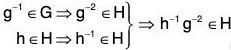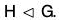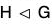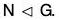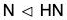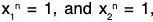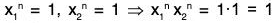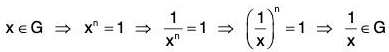Group Theory- II | Mathematics for Competitive Exams PDF Download
Subgroup
If a subset H of a group G is itself a group under the operation of G, we say H is subgroup of G. We use the notation H < G to mean H is a subgroup of G. If we want to indicate that H is a subgroup of G, but not equal to G itself, we write H < G. Such a subgroup is called a proper subgroup. The subgroup {e} is called the trivial subgroup of G, a subgroup that is not {e} is called a nontrivial subgroup of G.
Equation Zn under addition modulo n is not a subgroup of Z under addition, since addition modulo n is not the operation of Z
For example : The groups.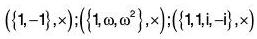
are contained in the group (C0, x) and are groups for its induced composition. Such groups are called subgroup of that large group. Thus we see that any sub group H of any group (G, x) is called for the composition of G and satisfies the axioms of the group for this composition, then that is called a subgroup of G
Subgroup Tests
When determining whether or not a subset H of a group G is a subgroup of G, one need not directly verify the group axioms.
One-Step Subgroup Test
Let G be a group and H a nonempty subset of G. Then, H is a subgroup of G if ab-1 is an H whenever a and b are in H. (In additive notation, H is a subgroup if a - b is in H whenever a and b are in H.)
Proof : Sine the operation of H is the same as that of G, it is clear that this operation is associative. Next, we show that e is in H. Since H is nonempty, we may pick some x in H. Then, letting a = x and b = x in the hypothesis, we have e = xx-1 is in H. To verify that x-1 is in H whenever x is in H, all we need to do is to choose a = e and b = x in the statement of the theorem. Finally, the proof will be complete when we show that H is closed; that is, if x, y belong to H, we must show that xy is in H also. Well, we have already shown that y-1 is in H whenever y is; so letting a = x and b = y-1, we have xy = x (y-1)-1 = ab-1 is in H.
Example : Let G be an Abelian group with identity e. Then H = {x ∈ G I x2 = e} is a subgroup of G Here, the defining property of H is the condition x2 = e. So, we first note that e2 = e so that H is non-empty. Now we assume that a and b belong to H. This means a2 = e and b2 = e. Finally, we must show that (ab-1)2 = e. Since G is Abelian, (ab-1)2 = ab-1ab-1 = a2 (b-1)2 = a2 (b2)-1 = ee-1 = e. Therefore, ab-1 belongs to H and, by the One-Step Subgroup Test, H is a subgroup of G.
Two-Step Subgroup Test
Let G be a group and H a nonempty subset of G. Then, H is a subgroup of G if ab ∈ H whenever a, b, ∈ H (closed under multiplication), and a-1 ∈ H whenever a ∈ H (closed under taking inverses).
Proof. By Theorem it suffices to show that a, b g H implies ab-1 ∈ H. So, we suppose that a, b ∈ H. Since H is closed under taking inverses, we also have b-1 ∈ H. Thus, ab-1 ∈ H by closure under multiplication.
Finite Subgroup Test
Let H be a nonempty finite subset of a group G. Then, H is a subgroup of G if H is closed under the operation of G.
Proof. In view of Theorem we need only prove that a~ 1 g H whenever a g H. If a = e, then a-1 = a and we are done. If a ≠ e, consider the sequence a, a2, a3, ... Since H is finite and closure implies that all positive powers of a are in H, not all of these elements are distinct. Say, ai = aj and i > j. Then ai-j = e; and since a ≠ e, i - j > 1. Thus, ai-j = a.ai-j-1 = e and, therefore ai-j-1 = a-1. But, i - j - 1 ≥ 1 implies ai-j-1 ∈ H and we are done.
Proper and Improper (or Trivial) subgroup
Every group G of order greater than 1 has atleast two subgroups which are :
(i) G (itself)
(ii) {e} i.e. the group of the identity alone.
The above two subgroups are known as improper or trivial subgroups.
A subgroup other than these two is known as a proper subgroup.
Important Remark : If any subset of the group G is a group for any operation other than the composition of G, then it is not called a subgroup of G.
For example, the group {1, - 1 } is a part o f (C, +) which is group for the multiplication but not for the composition (+) of the basic group. Therefore this is not the subgroup of (C, +).
Examples of Sub Group
- Additive Groups :
Example : (Z,+) is a subgroup of (Q,+)
Example : (Q,+) is a subgroup of (R,+).
Example : The set E of even integers is a proper subgroup of additive group (E,+), whereas the set O of odd integers is not a subgroup of the additive groups (Q,+), (Z,+).
Example : The set mZ of multiples of some given integer m is a sub group of (Z,+),
Example : The group {0, 4} is a subgroup of (Z8, +8) - Multiplicative Groups :
Example : (Q+, x) is a subgroup of (R+, x).
Example : {1, - 1 } , {1, ω, ω2}, {1, -1, i, - 1 } are subgroup of (C0, x), the group of non zero complex numbers
Example : For multiplication operation ({1, -1}, x) is a subgroup of {1, -1, i, -i}
Theorem : If H is a subgroup of a G, then :
- The identity of H is the same as that of G,
- The inverse of any element a of H is the same as the inverse of the same regarded as an element of G
- The order of any element a of H is the same as the order of a in G.
Proof.
- Let e and e’ be the identifies of G and H respectively.
If a ∈ H, then ae’ = e’ a = a ...(1)
Again a ∈ H ⇒ a ∈ G
∴ ae = ea = a ...(2)
From (1) and (2),
ae’ = ae
⇒ e’ = e [by cancellation law in G] - If e is the identity of G, so by (a) e is also the identity of H. Suppose that b and c are inverses of a in H and G respectively.

Therefore the inverse of any element of subgroup is the same as the of the subgroup and the original group. - Let the order of a ∈ H be m and n in H and G respectively. If e be the identity, then by the definition of order
am = e and an = e ⇒ am = an
⇒ am a-n = an a-n = a0
⇒ am-n = e
⇒ m - n = 0 [∵ m - n < m = O(a) in H]
⇒ m = n [m - n < n = O(a) in G]
Therefore, the order of any element of sub group is the same as that of the sub group and the original group.
In the above results, we conclude that a subset H of a group G is sub group iff :
(i) a ∈ H, b ∈ H, ⇒ ab ∈ H
(ii) e ∈ H where e is the identity of G
(iii) a ∈ H ⇒ a-1 ∈ H, where a-1 is the inverse of a in G.
Conversely : The above conditions are also sufficient because the conditions (ii) and (iii) show the existence of identity and inverse respectively and since the associative law holds in G, so also in H.
Algebra of complexes of a group
If H and K be two complexes of a group G, then their product HK and the inverse H-1 are defined as follows :
HK = {hk | h ∈ H, k ∈ K}
H-1 = {h~1 | h ∈ H}
For example, if H = {-2, 4}, K = {1, 3} are two complex of the group(Z, +), then HK = {(-2 + 1), (-2 + 3), (4 + 1), (4 + 3)}
= {-1, 1. 5, 7}
H-1 = {-2(-1), -4} = {2, -4}
and K-1 = {-1, -3}
Properties of Complexes
The following properties can be easily established for the complexes H, K and L of the group G:
- (a) (HK) L = H(KL) [Associativity]
(b) (HK)-1 = K-1 H-1 - If H is a subgroup of G, then :
(a) H-1 = H (but not conversely)
(b) HH = H
Remark : If HK = KH, then it does not mean that
hk = hk, ∀ h ∈ H, k ∈ K
∴ a ∈ H, b ∈ H ⇒ a ∈ H, b-1 ∈ H
⇒ ab-1 ∈ H [by closure property in H]
Therefore if H is a sub group of G, then the condition is necessary
Conversely : Suppose the given condition is true in H, then we shall prove that H will be a sub group.
∵ H ≠ φ
∴ Let a ∈ H
Now by the given condition,
a ∈ H, a-1 ∈ H ⇒ aa-1 = e ∈ H
Therefore identity exists in H.
Again by the same condition,
e ∈ H, a-1 ∈ H ⇒ ea-1 = a-1 ∈ H
Thus the inverse of every element exist in H.
Finally, a ∈ H, b ∈ H ⇒ a ∈ H, b-1 ∈ H
⇒ a(b-1)-1 = ab ∈ H
H is closed for the operation of G.
Therefore H is a sub group of G which proves that the given condition is sufficient of H to be a sub group.
Remark. If the operation of the group is addition (+), then the above condition will be :
a ∈ H, b ∈ H ⇒ (a - b) ∈ H
Using the complex property, the above condition may also be written in the form of the following corollary:
A nonvoid subset of H of a group G is a subgroup iff :
(a) HH-1 ⊂ H (b) HH-1 = H
Criterion for a finite complex to be a sub group
Theorem : A nonvoid finite subset H of a group G is a subgroup if a ∈ H, b ∈ H ⇒ ab ∈ H
Proof : Let H be a finite sub group of the group G, then H will be closed for the operation of G.
So a ∈ H, b ∈ H ab ab ∈ H
Conversely : If a ∈ H, b ∈ H ab ∈ H,
then a ∈ H aa = a2 ∈ H
Again a ∈ H, a2 ∈ H ⇒ aa2 = a3 ∈ H
Thus we will see that
an-1 ∈ H, a ∈ H ⇒ an ∈ H, ∀ n ∈ N
Therefore a, a2, a3, .... an, ... are all elements of H. But H is a finite sub set of G, so all the powers of a can not be distinct.
Cor : A nonvoid finite subset H of a group G is a subgroup iff HH = H.
Important Remark : It should be noted that the above condition is necessary for all groups (finite or infinite) but it is not sufficient for infinite groups.
Example : N is an infinite subset of the group (Z, +) which satisfies the above conditions but is not a sub group because the identity 0 ∈ N
Example : Let (G = {2n | n ∈ Z}, x) and H = {1, 2, 22, 23, . . . } then H ⊆ G and closed wrt multiplication but it is not a sub group of G because the multiplicative inverse of 2 i.e. (1/2) ∉ H.
Example : {1, -1} is a finite subgroup of (Q0, x)
Intersection of subgroups
Theorem : The intersection of any two subgroups of a group G is again a subgroup of G.
Proof. Let H1 and H2 be two sub groups of a group G.
∵ e ∈ H1, e ∈ H2 ⇒ e ∈ H1 ∩ H2 ⇒ H1 ∩ H2 ≠ φ
Now let a, b ∈ H1 ∩ H2, then
a, b ∈ H1 ∩ H2 ⇒ a, b ∈ H1 and a, b ∈ H2
⇒ ab-1 ∈ H1 and ab-1 ∈ H2 [∵ H1 and H2 are subgroups]
⇒ ab-1 ∈ H1 ∩ H2
∴ H1 ∩ H2 is a subgroup of G.
Generalisation
If H1, H2, .... Hn be a finite family of sub groups of G; then H1 ∩ H2 ∩ .... ∩ Hn is also a subgroup of G.
Most Important Remark
The union of two subgroups is not necessarily a subgroup.
For example, the group G = (Z, +) has two subgroups
H = 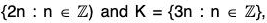 then their union
then their union
HUK = {... -6, -4, -3, -2, 0, 2, 3, 4, 6, ...}
is not a subgroup of G because this is not closed for +.
For example, 2 ∈ H ∪ K, 3 ∈ H ∪ K
but their 2 + 3 = 5 ∉ H ∪ K
which shows that H ∪ K is not closed for addition.
Theorem : The union of two subgroups is a subgroup iff one is contained in the other.
Proof. Let H1 and H2 be two subgroups of a group G.
First suppose that H1 ∪ H2 is a subgroup of G, then we have to show that either H1 ⊂ H2, or H2 ⊂ H1.
Now let us suppose that H1 ⊂ H2,
then H1 ⊄ H2 ⇒ ∃ a ∈ H1 and a ∉ H2 ...(1)
Let b ∈ H2, then
a ∈ H1, b ∈ H2 ⇒ a ∈ H1 ∪ H2 and b ∈ H1 ∪ H2
⇒ ab ∈ H1 ∪ H2 [∵ H1 ∪ H2 is a subgroup]
⇒ ab ∈ H1 or ab ∈ H2
Now ab ∈ H2, b ∈ H2 ⇒ (ab)b-1 = a ∈ H2
which contradicts our assumption (1).
Therefore ab ∉ H2. Hence ab ∈ H1
But ab ∈ H1 ⇒ a-1 (ab) = b ∈ H1
⇒ H2 ⊂ H1
Conversely : Now suppose that H1 ⊂ H2 or H2 ⊂ H1, then H1 ∪ H2 = H2 or H1
⇒ H1 U H2 is also a subgroup of G.
Criteria for the product of two subgroups of a group G
Theorem : Let H, K be subgroups of a group G. Then HK is a subgroup of G if and only if HK = KH.
Proof. Let HK = KH, then we shall prove that HK is a subgroup of G
∵ (HK)(HK)-1 = (HK)(K-1 H-1) [∵ (HK)-1 = K-1 H-1]
= H(KK-1)H-1 [by associativity]
= (HK)H-1 [∵ K is a subgroup ⇒ KK-1 = K]
= (KH)H-1 [∵ HK = KH]
= K(HH-1)
= KH [∵ H is a subgroup ⇒ HH-1 = H]
= HK
∴ HK is a subgroup of G.
Conversely : Now let HK be a subgroup of G, then
HK is a subgroup ⇒ (HK)-1 = HK
⇒ K-1 H-1 = HK
⇒ KH = HK [∵ H, K are subgroups ⇒ H-1 = H, K-1 = K]
Therefore HK is a sub group ⇔ HK = KH
Corollary : If H and K are subgroups of a commutative group then HK is a subgroup of G.
Proof : ∵ G is abelian ⇒ HK = KH ⇒ HK is a subgroup
Example : Prove that the set of the nth roots of unity is a subgroup of the multiplicative group 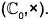
Let H =
be n complex numbers in H.
Therefore H is a non empty subset ofthen x, y ∈ H ⇒ xn = 1 and yn = 1
⇒ xn.(1/yn) = 1.1. = 1
⇒ (x/y)n = 1 ⇒ (xy-1)n = 1
⇒ xy-1 ∈ H
∴ H is a subgroup of (C0, x).
Example : Prove that H = {a + ib | a, b e 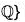 is a subgroup of the group
is a subgroup of the group
Clearly H is a non empty subset of C.
Let x, y ∈ H where x = a1 + ib1, y = a2 + ib2
then x - y = (a1 + ib1) - (a2 + ib2)
= (a1 - a2) + i(b2 - b2) ∈ H [∵ a1 - a2 ∈ Q, b1 - b2
∴ x ∈ H, y ∈ H ⇒ (x - y) ∈ H
Therefore H is a subgroup of (C, +).
Example : Prove that H is a subgroup of the group (C0, x) where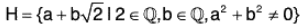
Clearly H is a non empty subset of C0.
Let x, y ∈ H where x = a1 + b1√2 and y = a2 + b2√2
then
Now ifwhich is false.
Therefore
Consequentlyare rational.
Therefore xy-1 ∈ H. Hence H is a sub group of
Example : Show that H is a subgroup of G for matrix multiplication :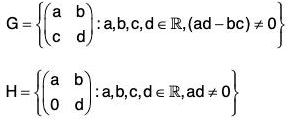
Clearly H is a non empty subset of G.
Let A, B ∈ G wherea1, a2, b1, b2, d1, d2 ∈ R, a1d1 ≠ 0 a2d2 ∈ 0
then
∴[∵ a2d2 ≠ 0, d2 ≠ 0]
Thus we see that A ∈ H, B ∈ H ⇒ AB-1 ∈ H
Therefore, H is a subgroup of G.
Example : If a is an element of a group G, then prove that its normalizer N(a) = {x ∈ Glax = xa} is a subgroup of G :
∵ e ∈ G ⇒ ae = ea ⇒ e ∈ N(a) ⇒ N(a) ≠ φ
Therefore let x1 x2 ∈ N(a), then by definition of N(a)
ax1 = x1a and ax2 = x2a
Now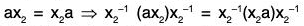
⇒
⇒
⇒
⇒
∴
Again[by associativity]
[∵ x1 ∈ N(a)]
[by associativity]
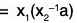
[by associativity]
∴
Thus we see that
Therefore N(a) is a subgroup of G.
Example : For any group G, prove that its centre Z(G) = {x ∈ GI xg = gx, ∀ g ∈ G} is a subgroup of G.
∵ e ∈ Q ⇒ eg = ge, ∀ g ∈ G
⇒ e ∈ Z(G) ⇒ Z(G) ≠ φ
Therefore let x1, x2 ∈ Z(G)
∴ x1g = gx1 and x2g = gx2, ∀ g ∈ G
Now
⇒
⇒
⇒
⇒
∴
Again[by associativity]
= x1(gx2-1) [∵ x2-1 ∈ Z(G)]
= (x1g)x2-1 [by associativity]
= (gx1)x2-1 [∵ x1 ∈ Z(G)]
= g(x1x2-1) [by associativity]
∴ x1x2-1 ∈ Z(G)
Thus we see that
x1 ∈ Z(G), x2 ∈ Z(G) ⇒ x1x2-1 ∈ Z(G)
Therefore Z(G) is a subgroup of G.
Example : Let G be the set of all ordered pairs (a, b) of real numbers for which a ≠ 0. Let a binary operation * on G be defined by (a, b) * (c, d) = (ac, be + d). Does the subset H of all those elements of G which are of the form (1, b) form a subgroup of G ?
If (a, b) ∈ G, then a ≠ 0
∴
Again
and
∴∈ G is the inverse of (a, b)
Thus the inverse of every element of G also exist in G.
Hence (G, o) is a group.
Clearly H is a non empty subset of G
Let (1, b),(1, c) ∈ H, then
= (1, b)*(1, -c)= (1, b-c)[by def of * on G]
But (1, b - c) is definitely an element of H.
Therefore, (1, b),(1, c) ∈ H ⇒ (1, b)*(1, c)-1 ∈ H
Hence H is a subgroup of G.
Examples of Subgroups
- <a> Is a Subgroup
Let G be a group, and let a be any element of G. Then, <a> is a subgroup of G.
Proof : Since a ∈ <a>, <a> is not empty. Let an, am ∈ <a>. Then, an (am)-1 = an-m ∈ <a> ; so, by Theorem <a> is a subgroup of G.
Example : In U (10), <3> = {3, 9, 7, 1} = U (10), for 31 = 3, 32 = 9, 33 = 7, 34 = 1, 35 = 34.3 = 1-3, 36.32 = 9, 3-1 = 7 (since 3.7 = 1), 3-2 = 9, 3-3 = 3, 3-4 = 1, 3-5 =3-4.3-1 = 1.7, 3-6 = 3-4.3-2 = 1.9 = 9,... - Center of a Group
The center, Z(G), of group G is the subset of elements in G that commute with every element of G. In symbols,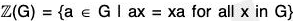
- Center Is a Subgroup
The center of a group G is a subgroup of G.
Proof : For variety, we shall use Theorem to prove this result. Clearly, e ∈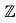 (G), so
(G), so  (G) is nonempty. Now, suppose a, b ∈
(G) is nonempty. Now, suppose a, b ∈ 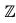 (G). Then (ab)x = a(bx) = a(xb) = (ax)b = (xa)b = x(ab) for all x in G ; and, therefore, ab ∈
(G). Then (ab)x = a(bx) = a(xb) = (ax)b = (xa)b = x(ab) for all x in G ; and, therefore, ab ∈ 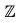 (G).
(G).
Next, assume that a ∈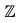 (G). Then, we have ax = xa for all x in G. What we want is a-1x = xa-1 for all x in G. Informally, all we need do to obtain the second equation from the first one is simultaneously to bring the a’s across the equal sign:
(G). Then, we have ax = xa for all x in G. What we want is a-1x = xa-1 for all x in G. Informally, all we need do to obtain the second equation from the first one is simultaneously to bring the a’s across the equal sign: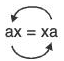 becomes xa-1 = a-1x. (Be careful here; groups need not be commutative. The a on the left comes across as a-1 on the left and the a on the right comes across as a-1 on the right.) Formally, the desired equation can be obtained from the original one by multiplying it on the left and right by a-1, like so:
becomes xa-1 = a-1x. (Be careful here; groups need not be commutative. The a on the left comes across as a-1 on the left and the a on the right comes across as a-1 on the right.) Formally, the desired equation can be obtained from the original one by multiplying it on the left and right by a-1, like so:
a-1(ax)a-1 = a-1(xa)a-1,
(a-1a)xa-1 = a-1x(aa-1),
exa-1 = a-1xe,
xa-1 = a-1x.
This shows that a-1 ∈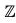 (G) whenever a is.
(G) whenever a is. - Centralizer of a in G
Let a be a fixed element of a group G. The centralizer of a in G, C(a), is the set of all elements in G that commute with a. In symbols, C(a) = {g ∈ G | ga = ag}. - C(a) Is a Subgroup
For each a in a group G, the centralizer of a is a subgroup of G is defined as
CG(A) = {g ∈ G : gag-1 = a, ∀a ∈ A}
NOTE : Normalizer and Centralizer are same for an element. Their difference can be understood only if you define them for a subset of a Group.
Normalizer of a subset A of G is defined to be NG(A) = {g ∈ G : gag-1 ∈ A, ∀a ∈ A}.
Normal Subgroup
We have seen that if H is a sub group of a group G, then, in general aH ≠ Ha, a ∈ G is an abelian group, then it holds good for every subgroup of such a group. We may also have subgroups H of a non abelian group G which satisfy aH = Ha, ∀ a ∈ G,.
Therefore such a subgroup for which every left coset is equal to its corresponding right coset is named as Normal Subgroup and it plays a very important role in the further studies. We shall now define such a subgroup in a slightly different form which will be more helpful to derive its certain properties.
Definition
A subgroup H of a group G is called a normal subgroup of G if aH = Ha for all a in G. We denote this by 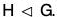
Many students make the mistake of thinking that “ H is normal in G” means ah = ha for a ∈ G and h ∈ H. This is not what normality of H means; rather, it means that if a ∈ G and h ∈ H, then there exists some h' ∈ H such that ah = h’a.
Proper and Improper Normal subgroups
It can be observed that every group G has atleast following two normal subgroups :
(ii) G itself
and (ii) {e}, the group consisting of the identity alone.
These two subgroups are called Improper normal subgroup of G and a normal subgroup other than these two is called a Proper normal subgroup.
Simple Groups
A group which has no proper normal subgroups is called a simple group
Example : Every group of prime order is simple because such a group has no proper subgroup.
Hamiltonian Group
If all the subgroups of a non Abelian group are normal, then called Hamiltonian group.
Remarks : The normal subgroup is also called a special subgroup or invariant subgroup or self conjugate subgroup.
Some properties of Normal subgroups
Theorem : Every subgroup of an abelian group is a normal group.
Proof. Let H be a subgroup of any commutative group G.
If x ∈ G and h ∈ H, then
xhx-1 = (hx)x-1 [∵ G is commutative]
= h(xx-1) [by associativity]
= he = h ∈ H
Thus, x ∈ G, h ∈ H ⇒ xhx-1 ∈ H,
∴ H is a normal subgroup of G.
Corollary. Every subgroup of a cyclic group is a normal subgroup.
Theorem : A subgroup H of a group G is a normal subgroup iff :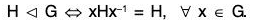
Proof. Let 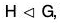 , then
, then
x ∈ G, h ∈ H ⇒ xhx-1 ∈ H
⇒ xHx-1 ⊂ H ...(1)
Again ∀ x ∈ G, xHx-1 ⊂ H ⇒ x-1 ⊂ H ...(1)
⇒ x-1Hx ⊂ H 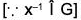
⇒ x(x-1Hx)x-1 ⊂ xHx-1
⇒ (xx-1)H(xx-1) ⊂ xHx-1
⇒ H ⊂ xHx-1 ...(2)
(1) and (2) ⇒ xHx-1 = H.
∴ 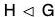 ⇒ xHx-1 = H, ∀ x ∈ G.
⇒ xHx-1 = H, ∀ x ∈ G.
Conversely : Let xHx-1 = H, ∀ x ∈ G.
then xHx-1 = H ⇒ xHx-1 ⊂ H
⇒ xhx-1 ∈ H, ∀ h ∈ H, x ∈ G.
∴ 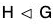
Hence 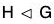 ⇔ xHx-1 = H, ∀ x ∈ G.
⇔ xHx-1 = H, ∀ x ∈ G.
Theorem : A subgroup H of a group G is a normal subgroup iff each left coset of H is right coset of H (and hence also iff each right coset of H is a left coset of H) i.e.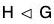 ⇔ xH = Hx, ∀ x ∈ G
⇔ xH = Hx, ∀ x ∈ G
Proof. Let 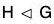 , then by theorem
, then by theorem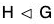 ⇒ xHx-1 = H, ∀ x ∈ G.
⇒ xHx-1 = H, ∀ x ∈ G.
⇒ (xHx-1)x = Hx
⇒ (xH)(x-1x) = Hx
⇒ xH = Hx, ∀ x ∈ G.
Conversely : If xH = Hx, ∀ x ∈ G, then
xH = Hx ⇒ xHx-1 = Hxx-1
⇒ xHx-1 = He = H
⇒ 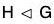
Therefore 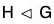 ⇔ xH = Hx, ∀ x ∈ G.
⇔ xH = Hx, ∀ x ∈ G.
Example : A subgroup H of a group G, is a normal subgroup of G iff the product of two right (left) cosets of H in G is again a right (left) coset of H in G.
Proof. Let 
If a, b ∈ G then Ha and Hb are two right cosets of H in G.
Let h1a ∈ Ha and h2b ∈ Hb, then
h1ah2b ∈ HaHb
But h1ah2b = h1(ah2)b
= h1(h2a)b [∵ Ha = aH ⇒ ah2 = h2 a, h2 ∈ H]
∴ HaHb ⊂ Hab ...(1)
Again for every h ∈ H
h(ab) = (ha)b = (ha)eb ∈ Ha Hb
∴ Hab ⊂ HaHb ...(2)
Hence (1) and (2) ⇒ Ha Hb = Hab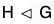 ⇒ HaHb = Hab.
⇒ HaHb = Hab.
Conversely : Suppose that the product of two right cosets of H is again a right coset of H in G. Let x ∈ G then Hx and Hx-1 are two right cosets of H in G. Then as supposed HxHx-1 is also a right coset of H in Q
Now x ∈ Hx and x-1 ∈ Hx-1 ⇒ xx-1 ∈ HxHx-1 = Hy (say)
⇒ e ∈ Hy.
But H itself is a right coset of H containing e and any two right cosets are either identical or disjoint, so
HxHx-1 = Hy = H, ∀ x ∈ G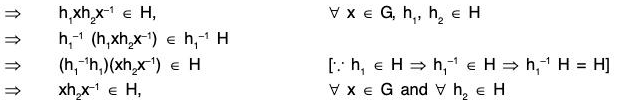
⇒ H is a normal subgroup.
Theorems on normal subgroup
Theorem : The intersection of any two normal subgroups of a group is a normal subgroup.
Proof. Let H1 and H2 be two normal subgroups of a group G.
Earlier we have seen that the intersection of two subgroups of a group G is again a subgroup, so H1 ∩ H2 is also a subgroup of G.
Now if x ∈ G and h ∈ H1 ∩ H2,
then h ∈ H1 ∩ H2 ⇒ h ∈ H1 and h ∈ H2
Now, since 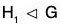
∴ x ∈ G, h ∈ H1 ⇒ xhx-1 ∈ H1.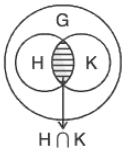 Similarly
Similarly 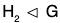
∴ x ∈ G, h ∈ H2 ⇒ xhx-1 ∈ H2.
Thus we see that
x ∈ G, h ∈ H1 ∩ H2 ⇒ xhx-1 ∈ H and xhx-1 ∈ H2
⇒ xhx-1 ∈ H1 ∩ H2
∴ H1 ∩ H2 G
G
Corollary. The intersection of any finite family of normal subgroups is a normal subgroup
Theorem. If H is a subgroup of G and N < G, then H ∩ N 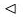 H.
H.
Proof. Since intersection of two subgroup is also a subgroup,
So H ∩ N is also a subgroup of G.
Also H ∩ N ⊂ H, therefore H ∩ N is also a subgroup of H.
Let h ∈ H ∩ N and x ∈ H,
then h ∈ H ∩ N ⇒ h ∈ H and h ∈ N
Again h ∈ H, x ∈ H ⇒ xhx-1 ∈ H [∵ H is a subgroup]
and h ∈ N, x ∈ H ⇒ h ∈ N, x ∈ G, [∵ H ⊂ G]
⇒ xhx-1 ∈ N. [∵ N is normal]
Therefore xhx-1 ∈ H, xhx-1 ∈ N ⇒ xhx-1 ∈ H ∩ N.
Thus we see that
h ∈ H ∩ N, x ∈ H ⇒ xhx-1 ∈ H ∩ N.
∴ 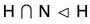
Theorem : If H and K are two normal subgroups of a group G, then 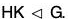
Proof. HK is a sub group of G :
∵  ∴ for every k ∈ K, k ∈ G
∴ for every k ∈ K, k ∈ G
Hk = kH ⇒ HK = KH.
⇒ HK is a subgroup of G. ...(1)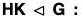
Let x ∈ G and hk ∈ HK, then
x(hk)x-1 = x(hx-1 xh)x-1
= (xhx-1)(xkx-1) ∈ HK. [∵ xhx-1 ∈ H, xhx-1 ∈ K]
Thus we see that
x ∈ G, hk ∈ HK ⇒ x(hk)x-1 ∈ HK.
From (1) and (2), 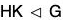
The existence of Normal Subgroups
Theorem : Every subgroup of a group with index 2 is a normal subgroups.
Let H be a subgroup of a group G such that its index is 2. Then, H has only two distinct right (left) cosets in G.
So let G = H ∪ Hx, where Hx ∩ H ≠ φ
Now, Hx ∩ H = φ and x ∈ Hx ⇒ x ∉ H
⇒ H and xH are also disjoint. [∵ x ∈ xH]
∴ G = H ∪ xH
then H ∪ H x = G = H ∪ xH ⇒ Hx = xH
⇒ 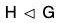
Example : Let G be a group and H be its subgroup generated by {x-1 y-1 xy | x, y ∈ G}. Show that 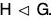
Let h ∈ H and g ∈ G, then h ∈ G, g ∈ G
Therefore h-1 ∈ G, g-1 ∈ G.
Now ghg-1 = (ghg-1 h-1h) = (ghg-1h-1)h
= [(g-1)-1(h-1)-1 g-1h-1]h
Here let g-1 = x, h-1 = y, then
ghg-1 = (x-1 y-1 xy)h ∈ H
Hence
Example : Let G be the group of all real matrices of types 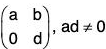 under matrix multiplication and N =
under matrix multiplication and N = 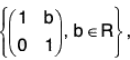 then prove that
then prove that 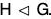
(i) N is a subgroup of G :
Let α, β ∈ N, whereand
then
Therefore[∵ b1 - b2 ∈ R]
Thus α ∈ N, β ∈ N ⇒ αβ-1 ∈ N.
∴ N is a subgroup of G.(ii)
Again ifthen
∴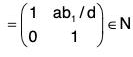
Thus γ ∈ G, α ∈ N ⇒ γαγ-1 ∈ N.
∴
Example : If H is a subgroup of a group G such that x2 ∈ H, ∀ x ∈ G, then prove that 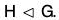 .
.
Let g ∈ G and h ∈ H.
Then g ∈ G, h ∈ H ⇒ gh ∈ G
⇒ (gh)2 ∈ H [by the given property]
Again
and (gh)2 ∈ H, h-1 g-2 ∈ H ⇒ (gh)2h-1g-2 ∈ H
⇒ ghghh-1 g-1 g-1 = ghg-1 ∈ H
Thus g ∈ G, h ∈ H ⇒ ghg-1 ∈ H
⇒
Example : If 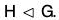 and K
and K 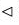 G such that H ∩ K = {e}, then show that hk = kh for every h ∈ H and k ∈ K.
G such that H ∩ K = {e}, then show that hk = kh for every h ∈ H and k ∈ K.
Since H and K are subgroups, therefore
h ∈ H ⇒ h-1 ∈ H and k ∈ K ⇒ k-1 ∈ K
Now, h-1 ∈ H, k ∈ G ⇒ kh-1 k-1 ∈ H [∵]
⇒ h(kh-1k-1) = hkh-1 k-1 ∈ H [∵ h ∈ H]
Again k ∈ K, h ∈ G ⇒ hkh-1 ∈ K
⇒ (hkh-1)k-1 = hkh-1 k-1 ∈ K
Thus hkh-1 k-1 ∈ H and hkh-1 k-1 ∈ K
⇒ hkh-1 k-1 ∈ H ∩ K
⇒ hkh-1 k-1 = e
⇒ hk = kh.
Example : If H is the only subgroup with finite order in a group G, then prove that 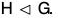
We have already proved that for any x ∈ G, xHx-1 is a subgroup of G. Since H is a subgroup of finite order, therefore let
O(H) = m and H = {h1, h2, .... hm}
∴ xHx-1 = {xh1x-1, xh2x-1, ..., xhmx-1}
∵ xhix-1 = xhjx-1 ⇒ hi = hj [by cancellation law in H]
Therefore all the elements in xHx-1 are different.
Hence O(xHx-1) = m = O(H)
But H is the only subgroup of finite order in G, therefore
xHx-1 = H ⇒
Example : Let H and N be subgroup and normal subgroup of a group G respectively, then prove that 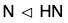
Suppose identity e ∈ H and for any arbitrary x ∈ N
Again n1 be any arbitrary element of HN, such that
h ∈ H and n ∈ N
Again n1 be any arbitrary element of N, then
(hn)n1 (hn)-1 = hn n1n-1h-1 = h(nn1n-1)h-1 ...(1)
SinceTherefore nn1n-1 ∈ N, ∀ n ∈ G and n1 ∈ N and consequently, in particular nn1n-1 ∈ N, ∀ n ∈ N and n1 ∈ N
Therefore h ∈ H, nn1n-1 ∈ N ⇒ h ∈ G, nn, n-1 ∈ N
⇒ h(nn1n-1)h-1 ∈ N
Therefore by (1), (hn)n(hn)-1 ∈ N, ∀ hn ∈ HN and n ∈ N
Hence
Normal Subgroup Test
A subgroup H of G is normal in G if and only if xHx-1 ⊆ H for all x in G.
Example : Every subgroup of an Abelian group is normal. (In this case, ah = ha for a in the group and h in the subgroup.)
Example : The center Z(G) of a group is always normal. (Again, ah = ha for a ∈ G and h ∈ Z(G).)
Cyclic Groups
Definition : A group G is called a cyclic group if all of its element can be express as power of a single element say a ∈ G.
In this case ‘a’ is called to be a generator of G. i.e. if ‘a’ is generator then for x ∈ G there is an integer k such that ak = x
Let G be a finite group of order n then G = {a, a2, a3, ..., an-1, an = e}.
Note that order of cyclic group is equal to the order of its generator and the generating element is not necessary unique.
e.g. {±1, ±i}.
Let a = i,
a2 = i2 = -1
a3 = i3 = i • i2 = -i
a4 = (i2)2 = 1
Also if a = -i, then this is also generator i.e. i, - i are a generator.
Theorem : If a is an element of a group G, then : 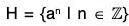 is a subgroup of G.
is a subgroup of G.
Proof. Let x, y ∈ H where x = ap, y = aq p, q ∈
then xy-1 = ap(aq)-1 = ap.a-q = ap-q ∈ H [∵ p - q ∈ 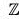 ]
]
∴ x ∈ H, y ∈ H ⇒ xy-1 ∈ H
Therefore H is a sub group of G.
From this theorem it is clear that every element of the group G generates a sub group which is called cyclic group.
For every element a of the group G
H = {an | n ∈ 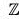 }
}
is a subgroup of G which is called cyclic group generated by a.
It is denoted by [a].
A group G is called cyclic if there is an element a in G such that G = {an | n ∈ 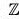 }. Such an element a is called a generator of G. we may indicate that G is a cyclic group generated by a by writing G = <a>.
}. Such an element a is called a generator of G. we may indicate that G is a cyclic group generated by a by writing G = <a>.
Example : The set of integers 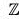 under ordinary addition is cyclic. Both 1 and -1 are generators. (Recall that, when the operation is addition, 1n is interpreted as
under ordinary addition is cyclic. Both 1 and -1 are generators. (Recall that, when the operation is addition, 1n is interpreted as
 when n is positive and as
when n is positive and as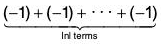 when n is negative.)
when n is negative.)
Examples of Cyclic Group
Example : 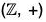 is an infinite cyclic group with 1 and -1 as its two generators.
is an infinite cyclic group with 1 and -1 as its two generators.
Example : The multiplicative group {1, - 1, i, - i }, x) is a finite cyclic group with i and - i as its two generators, because G = {i1 = i, i2 = -1, i3 = -i, i4 = 1} = [i] and G = {(-i)1= -i, (-i)2 = -1, (-i)3 = i,(-i)4 = 1} = [-i]
Example : The group [ 4 = {0, 1, 2, 3}, +4] is a cyclic group with 1 and 3 as its two generators, because
4 = {0, 1, 2, 3}, +4] is a cyclic group with 1 and 3 as its two generators, because 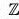 4 = (1(1) = 1, 2(1) = 2, 3(1) = 3, 4(1) = 0} = [1]
4 = (1(1) = 1, 2(1) = 2, 3(1) = 3, 4(1) = 0} = [1]
and 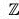 4 = (1(3) = 3, 2(3) = 2, 3(3) = 1, 4(3) = 0} = [3]
4 = (1(3) = 3, 2(3) = 2, 3(3) = 1, 4(3) = 0} = [3]
Properties of cyclic group
Theorem : Every cyclic group is abelian
Proof. Let G = [a] be a cyclic group and x, y ∈ G, then
x = am, y = an m, n ∈ 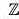
then xy = aman = am+n = an+m [∵ m + n = n + m]
= anam = yx
∴ G is an abelian group.
Remark : An abelian group need not be cyclic.
Example : (R,+) Is an abelian but not cyclic.
Theorem : If a is a generator of a cyclic group G, then a-1 is also its generator.
Proof. Let G = [a] be a cyclic group and x ∈ G
Since G is a cyclic group, so there exist an integer m such that
x = am ⇒ x = (a-1)-m, [- m ∈ Z]
⇒ x can also be expressed as some integral power of a-1
⇒ a-1 is also the generator of G.
Therefore G = [a] ⇒ G = [a-1]
Theorem : The order of a finite cyclic group is equal to the order of its generator i.e.,
Proof. Let G = [a] be a finite cyclic group and O(a) = n
Let H = {a, a2, a3,..,an = e}
Clearly H is a sub group of G whose order is n.
Case 1. When m ≤ n : If am ∈ G, then am ∈ H
∴ H ⊂ G ...(1)
Case 2. m > n : m = q n + r, 0 ≤ r < n, q, r ∈ 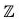
⇒ am = aqn+r [by division algorithm]
= (an)q • ar = ear
= ar ∈ H
∴ G ⊂ H ...(2)
(1) and (2) ⇒ G = H
But O(H) = n
∴ O(G) = n = O(a)
Corollary. A finite group of order n is cyclic iff it has an element of order n.
Proof. Let G = [a] be a finite cyclic group of order n.
Then by the above theorem, an element a exists in G such that
O(a) = O(G) = n
Conversely : Let G be a finite cyclic group of order n in which an element a exists such that O(a) = n
Now if H = [a], then H ⊂ G and by the above theorem O(a) = n ⇒ O(H) = n
⇒ O(H) = O(G)
Similarly, G is finite group such that
H ⊂ G and O(G) = O(H)
⇒ G = H = [a]
⇒ G is a cyclic group generated by a.
Theorem : Every infinite cyclic group has two and only two generators.
Proof. Let G = [a] be an infinite cyclic group. Then by theorem a-1 is also a generator of G.
To show : a ≠ a-1
Let a = a-1, then a = a-1
⇒ aa = a-1a ⇒ a2 = e
⇒ O(a) = 2 ⇒ O(G) = 2
which is not possible because G is an infinite group. Therefore a ≠ a-1
To show that G does not have any generator other than these two :
Let, if possible, am, m ≠ ± 1 be also a generator of g.
Then for a ∈ G there exists an integer n such that
a = (am)n = amn
⇒ aa-1 = amn a-1
⇒ e = amn-1
⇒ O(a) is finite.
⇒ O(G) is finite.
which contradicts that G is infinite.
Hence am can not a generator of G unless m = 1 or -1.
Consequently, G has exactly two generators a and a-1.
Theorem : Every subgroup of a cyclic group is also cyclic.
Proof. Let G = [a] be a cyclic group and H be a sub group of G. If H = G or H = {e}; then clearly H also cyclic.
If H is a proper sub group of G, then H contains at least one element am (m 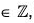 , m ≠ 0) other than the identity.
, m ≠ 0) other than the identity.
am ∈ H ⇒ a-m ∈ H [∵ H is a sub group]
Since m ≠ 0, therefore m > 0 or m < 0
⇒ There exist positive integral powers of a in H.
Let m be the least positive integer such that am ∈ H
To prove H = [am] :
Let an ∈ H, then by division algorithm, there exist two integers q and r such that n = mq + r, 0 ≤ r < m
or n - mq = r
Now since am ∈ H ⇒ (am)q = amq ∈ H
⇒ (amq)-1 = a-mq ∈ H
∴ an ∈ H, a-mq ∈ H ⇒ an • a-mq = an-mq ∈ H
⇒ ar ∈ H [∵ n-mq = r]
But m is the least positive integer such that am ∈ H and 0 ≤ r < m
Therefore r = 0 Consequently n = mq
and so an = amq = (am)q ⇒ H = [am]
Therefore every subgroup of G is cyclic.
Corollary. Every proper subgroup of an infinite cyclic group is infinite.
Proof. Let G = [a] be an infinite cyclic group and H be a proper sub group of G. Then by the above theorem H is cyclic and H = [am]
where m is the least positive integer such that am ∈ H
Let, if possible,
O(H) = p, (p ∈ N)
then O(H) = p ⇒ O(am) = p
⇒ (am)p = e
⇒ amp = e
⇒ O(a) is finite
⇒ O(G) is finite.
which is contrary to the hypothesis. Therefore the order of H can not be finite. Consequently every proper subgroup of G is infinite.
Theorem : If G = [a] is a cyclic group of order n and H = [as], then H is a cyclic subgroup of G is of order n/d where d is HCF of n and s.
Proof. Let O(H) = m
then O(H) = m ⇒ O(as) = m
⇒ (as)m = ams = e
⇒ O(a) | ms
⇒ n | ms [∵ O(G) = n ⇒ O(a) = n]
Therefore d = HCF of {n, s}
Therefore there exist two integers r and q which are relatively prime.
and n = rd and s = qd ...(1)
Now N | ms ⇒ rd | m(qd)
⇒ r | mq
⇒ r | m or r | q
⇒ r | m [∵ r and q are relatively prime] ...(2)
Again (as)r = ars = arqd = aq(rd) = aqn
⇒ (as)r = aqn = (an)q = e
⇒ O(as) | r
= m | r ...(3)
From (1), (2) and (3), m = r = n/d
O(H) = n/d
Corollary. If a is a generator of a finite cyclic group of order n, then the other generators of G are of the form ar, where r is relatively prime to n.
Proof. ∵ O(G) = O(a) = n
∴ 0[ar[ = n/d, where d is HCF of n and r. [by the above theorem]
If ar is also a generator of G, then
G = [a] = [ar] ⇒ O[a] = O[ar]
⇒ n = n/d
⇒ d = 1
⇒ r is relatively prime to n.
Corollary. Every finite cyclic group of composite order posses proper subgroups.
Proof. Let G = [a] be a finite cyclic group of composite order.
O(G) = mn, n ≠ 1; n ≠ 1
If H = [am] then by the above theorem,
O(H) = (mn/m) = n < mn = O(G)
Therefore, H is a proper subgroup of G.
Example : Prove that group of order 3 is cyclic.
Let G = {e, a, b} be a group and a and b are different.
Now a ∈ G , b ∈ G ⇒ ab ∈ G [∵ closed]
Therefore, three possibilities are :
(1) ab = e or, (2) ab = a or, (3) ab = b
Now ab = a ⇒ b = e,
which is against the hypothesis that e is different from a and b.
Therefore ab ≠ a,
Similarly ab ≠ b
Hence ab = e ...(1)
Again a2 ∈ G. Therefore there are three possibilities :
(i) a2 = e or, (ii) a2 = a or, (iii) a2 = b
(1) If a2 = e, then by (1), a2 = ab ⇒ a = b [by cancellation law]
which is against our hypothesis. Therefore
a2 ≠ e
(2) Again a2 = a ⇒ a = e but a and e are different elements
Therefore a2 ≠ a and consequently a2 = b
∴ G = {e, a, a2}
Finally, a3 = aa2 = ab = e
Hence G is cyclic and a is its generator.
Example : Prove that the set G = {x | xn = 1} of nth roots of unity is a finite multiplicative cyclic group of order n.
Let x1, x2 ∈ G,
then
But
⇒ (x1x2)n = 1
⇒ x1x2 ∈ G
∴ x1 ∈ G, x2 ∈ G ⇒ x1x2 ∈ G
So G is closed for multiplication.
Also 1n = 1 ⇒ 1 ∈ G which is the identity for multiplication.
Further for each x ∈ G,
which is the inverse of x. So each element of G is invertible.
Lastly, the multiplication of numbers is associative, so it is also associative in G. Hence G is a group for multiplication.
∵ xn = 1 has exactly n roots, So O(G) = n
G is a Cyclic group : ∵ 1 = cos 2mπ + sin 2mπ, m ∈
Therefore G is a cyclic group of order n generated by e2πi/n.
Example : Find all the generators of the cyclic group
(G = { 0 , 1 , 2, 3, 4, 5}, +6)
We find that
1(0) = 0 ⇒ O(0) = 1
1(1) = 1, 2(1) = 2, 3(1) = 3, 4(1) = 4, 5(1) = 5, 6(1) = 0 ⇒ O(1) = 6
1(2) = 2, 2(2) = 4, 3(2) = 0 ⇒ O(2) = 3
1(3) = 3, 2(3) = 0 ⇒ O(3) = 2
1(4) = 4, 2(4) = 2, 3(4) = 0 ⇒ O(4) = 3
1(5) = 5, 2(5) = 4, 3(5) = 3, 4(5) = 2, 5(5) = 1, 6(5) = 0 ⇒ O(5) = 6
Observing the orders of all the elements of G, we find
O(1) = O(5) = 6 = O(G)
Therefore G = [1] = [5] i.e. 1 and 5 are two generators of g.
Example : Find all the generators of the cyclic group (G = {1, 2, 3, 4}, x5)
Here we have O(G) = 4. Its generator is the element of G whose order is 4.
We have 1 = 1 ⇒ O(1) = 1
21 = 2, 22 = 4, 23 = 3, 24 = 1 ⇒ O(2) = 4
31 = 3, 32 = 4, 33 = 2, 34 = 1 ⇒ O(3) = 4
42 = 1 ⇒ O(4) = 1
Clearly, 2, 3 ∈ G such that
O(2) = 4 = O(G) and O(3) = 4 = O(G)
⇒ 2 and 3 are two generators of the cyclic group G.
Example : Find all the generators of the cyclic group of order
(a) 8 (b) 12
(a) Let G = [a] be a cyclic group of order 8.
By theorem the other generators of G will be of the form am where m < 8 relatively prime number.
So m = 3, 5, 7
Therefore all the generators of G are : a, a3, a5, a7
(b) Again let G = [a] be a cyclic group of order 12.
The other generators of G will be of the form am
where m < 12 and is relatively prime number.
So m = 5, 7, 11
Therefore all the generators of G are : a, a5, a7, a11.
Theorem : Criterion for ai = aj
Let G be a group, and let a belong a belong to G. If a has infinite order, then all distinct powers of a are distinct group elements. If a has finite order, say, n, then <a> = {e, a, a2, ..., an-1} and ai = aj if and only if n divides i - j.
Proof : If a has infinite order, there is no non-zero n such that an is the identity. Since ai = aj implies ai-j = e, we must have i - j = 0, and the first statement of the theorem is proved.
Now assume that |a| = n. We will prove that <a> = {e, a, ... an-1}. Certainly, the elements e, a, ..., an-1 are distinct. For if ai = aj with 0 ≤ j < i ≤ n - 1, then ai-j = e. But this contradicts the fact that n is the least positive integer such that an is the identity.
Now, suppose that ak is an arbitrary member of <a>. By the division algorithm, there exist integers q and r such that
k = qn + r with 0 ≤ r < n.
Then ak = aqn+r = aqn • ar = (an)q • ar = ar, so that ak ∈ {e, a, a2, ... an-1}. This proves that <a> = {e, a, a2, .... an-1}.
Next, we assume that ai = aj and prove that n divides i - j. We begin by observing that ai = aj implies ai-j = e. Again, by the division algorithm, there are integers q and r such that
i - j = qn + r with 0 ≤ r ≤ n.
Then ai-j = aqn+r and, therefore, e = ear = ar. Since n is the least positive integer such that an is the identity, we must have r = 0 so that n divides i - j.
Conversely, if n divides i - j, then ai-j = anq = eq = e so that ai = aj.
Corollary : ak = e Implies that |a| Divides k
Let G be a group and let a be an element of order n in G. If ak = e, then n divides k.
Proof : Since ak = e = a0, we know by Theorem that n divides k - 0.
Generators of Cyclic Groups
Let G = <a> be a cyclic group of order n. Then G = <ak> if and only if gad(k, n) = 1.
Proof : If gcd(k, n) = 1, we may write 1 = ku + nv for some integers u and v. Then a = aku+nv = aku • anv = aku. Thus, a belongs to <ak> and therefore all powers of a belongs to <ak>. So, G = <ak> and ak is a generator of G.
Now suppose that gcd(k, n) = d > 1. Write k = td and n = sd.
Then (ak)s = (atd)s = (asd)t = (an)t = e, so that lakl ≤ s < n. This shows that ak is not a generator of G.
Generators of 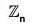
An integer k in 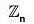 is a generator of
is a generator of 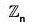 if and only if gcd(k, n) = 1.
if and only if gcd(k, n) = 1.
Classification of Subgroups of Cyclic Groups
Fundamental Theorem of Cyclic Groups
Every subgroup of a cyclic group is cyclic. Moreover, if |<a>l = n, then the order of any subgroup of <a> is a divisor of n; and, for each positive divisor k of n, the group <a> has exactly one subgroup of order k-namely, <an/k>.
Corollary Subgroups of 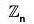
For each positive divisor k of n, the set <n/k> is the unique subgroup of 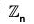 of order k; moreover, these are the only subgroups of
of order k; moreover, these are the only subgroups of 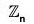 .
.
Example. The list of subgroups of Z30 is
<1> = {0, 1, 2, .... 29} order 30,
<2> = {0, 2, 4, 28} order 15,
<3> = {0, 3, 6, 27} order 10,
<5> = {0, 5, 10, 15, 20, 25} order 6,
<6> = {0, 6, 12, 18, 24} order 5,
<10> = { 0 , 10, 20} order 3,
<15> = {0, 15} order 2,
<30> = {0} order 1,
Theorem : Number of Elements of Each Order in a Cyclic Group
If d is a positive divisor of n, the number of elements of order d in a cyclic group of order n is φ(d).
Proof : By Theorem there is exactly one subgroup of order d-call it <a>. Then every element of order d also generates the subgroup <a> and, by Theorem an element ak generates <a> if and only if gcd(k, d) = 1. The number of such elements is precisely <φ>(d).
|
98 videos|34 docs|32 tests
|
FAQs on Group Theory- II - Mathematics for Competitive Exams
| 1. What is a subgroup? |  |
| 2. What is a normal subgroup? |  |
| 3. What are cyclic groups? |  |
| 4. How are subgroups related to normal subgroups? |  |
| 5. What is the significance of group theory in mathematics? |  |