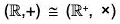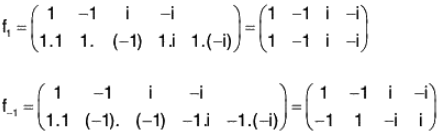Group Theory- IV | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Morphism |

|
| Group Homomorphism |

|
| FACTOR GROUPS |

|
| GROUP ACTION |

|
Morphism
In many fields of mathematics, morphism refers to a structure-preserving map from one mathematical structure to another. The notion of morphism recurs in much of contemporary mathematics. In set theory, morphisms are functions; in linear algebra, linear transformations; in group theory, group homomorphisms; in topology, continuous functions, and so on.
In category theory, morphism is a broadly similar idea, but somewhat more abstract: the mathematical objects involved need not be sets, and the relationship between them may be something more general than a map, although has to behave similarly to maps, e.g. has to admit associative composition.
The study of morphisms and of the structures (called "objects") over which they are defined is central to category theory. Much of the terminology of morphisms, as well as the intuition underlying them, comes from concrete categories, where the objects are simply sets with some additional structure, and morphisms are structure-preserving functions. In category theory, morphisms are sometimes also called arrows.
Some special morphisms
A morphism f of a group G into G’ is called :
- Monomorphism, If f is injection (one one).
- Epimorphism, If f is surjection (onto).
Here G’ is called the homomorphic image of the group G. - Isomorphism, If f is bijection (one one onto).
- Endomorphism, If G’ = G i.e., f is a homomorphism from G to itself.
- Automorphism, If G’ = G and f is bijection.
Group Homomorphism
Homomorphism
A mapping f from a group (G, *) to a group (G', o) is called a group homomorphism (or group morphism) from G to G’ if
f(a * b) = f(a) o f(b), ∀ a, b ∈ G.
Thus, if f is a morphism from G to G', then it preserves the composition in both the groups G and G’ i.e.,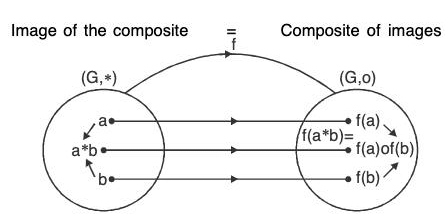
Example : Let  +) be the additive group of real numbers and
+) be the additive group of real numbers and 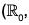 *) be the multiplicative group of non zero real numbers.
*) be the multiplicative group of non zero real numbers.
The mapping f : 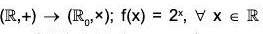 is a homomorphism of
is a homomorphism of  into
into 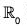 because for any x1, x2 ∈
because for any x1, x2 ∈ 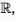
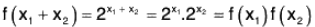
Various Morphisms
A morphism f of a group G into G’ is called
(i) Monomorphism, if f is injection (one one).
(ii) Epimorphism, if f is surjection (onto).
Here G’ is called the homomorphic image of the group G.
Example : Let G = {1, -1} be a multiplicative group. Then the map f : (Z, +) → (G, x)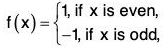
is an epimorphism from 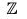 to G, because for any x1, x2 ∈
to G, because for any x1, x2 ∈ 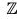
- when x1, x2 both are even, then f(x1 + x2) = 1 = 1.1 = f(x1).f(x2)
- when x1 is even and x2 is odd, then f(x1 + x2) = -1 = 1 (-1) = f(x1).f(x2)
- when x1 is even and x2 is odd, then f(x1 + x2) = -1 = 1.(-1) = f(x1).f(x2)
- when x1 is odd and x2 is even, then f(x1 + x2) = -1 = -1.1 = f(x1) f(x2)
Thus f(x1 + x2) = f(x1).f(x2), ∀ x1,x2 ∈ Z
Again f(Z) = G ⇒ f is onto.
Hence f is an epimorphism from Z onto G.
(iii) Isomorphism, if f is bijection (one one onto).
Example : For any group G, the identity mapping lG is an isomorphism of G onto itself, because for any x1,x2 in G and lG is obviously a bijection.
(iv) Endomorphism, if G’ = G i.e. f is a homomorphism from G to itself.
Example : The map f : 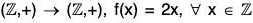 is a homomorphism from
is a homomorphism from 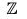 to itself because for x1, x2 ∈
to itself because for x1, x2 ∈ 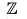
f(x1 + x2) = 2(x1 + x2) = 2x1 + 2x2 = f(x1) + f(x2)
(v) Automorphism, if G’ = G and f is bijection.
Properties of homomorphism
Theorem : If f is a homomorphism from a group G to G’ and if e and e’ be their respective identities, then :
(a) f(e) = e'
(b) f(a-1) = [f(a)]-1, ∀ a ∈ G
Proof : (a) Let a ∈ G, then ae = a = ea
⇒ f(ae) = f(a) = f(ea)
⇒ f(a) f(e) = f(a) = f(e) f(a) [∵ f is homomorphism]
⇒ f(e) is the identity in G’ ⇒ f(e) = e'
Therefore the image of the identity of G under the group morphism f is the identity of G’.
(b) Let a-1 be the inverse of a ∈ G, then
aa-1 = e = a-1 a ⇒ f(aa-1) = f(e) = f(a-1a)
⇒ f(a) f(a-1) = e’ = f(a-1) f(a) ⇒ f (a-1) = [f(a)]-1
therefore, the f-image of the inverse of any element of G under is the inverse of the f-image of a in G'.
Theorem : If f is a homomorphism of a group G to a group G’, then
(a) H is a subgroup of G ⇒ f(H) is a subgroup of G'.
(b) H’ is subgroup of G’ ⇒ f-1(H’) = {e ∈ G | f(x) ∈ H’} is a subgroup of G.
Proof : (a) Clearly f(H) ⊂ G’ and f(H) = φ, because
e ∈ H ⇒ f(e) = e’ ∈ f(H) where e’ is identity in G’
If a’, b’ ∈ f(H), then a’, b’ ∈ f(H) ⇒ there exist a, b in H such that
f(a) = a’ and f(b) = b’
⇒ a’(b’)-1 = f(a)[f(b)]-1
= f(a) f(b-1) [∵ [f(b)]-1 = f(b-1)]
= f(ab-1) [∵ f is homomorphism]
But a ∈ H, b ∈ H ⇒ ab-1 ∈ H
⇒ f(ab-1) ∈ f(H)
Thus a’, b ∈ f(H) ⇒ f(ab-1) = a’(b’)-1 ∈ f(H)
∴ f(H) is a subgroup of G’
(b) Obviously f-1(H’) ⊂ G and f-1(H’) ≠ φ because atleast e ∈ f-1 (H’)
If a, b ∈ f-1(H’), then
a, b ∈ f-1(H’) ⇒ f(a) ∈ H’ and f(b) ∈ H'
⇒ f(a)[f(b)]-1 ∈ H’ [∵ H is a subgroup]
⇒ f(a) f(b-1) ∈ H'
⇒ f(ab-1) ∈ H’ [∵ f is homomorphism]
⇒ ab-1 ∈ f-1 (H’)
Thus a, b ∈ f-1(H') ⇒ ab-1 ∈ f-1 (H’)
∴ f-1(H’) is a subgroup of G
Corollary : If f is a homomorphism from a group G to G \ then f(G) is a subgroup of G’.
This can be easily proved by taking H = G in part (a) of the above theorem.
Kernel of Homomorphism
Let f be a homomorphism of a group G into G', then the set K of all those elements of G are mapped to the identity e’ of G’ is called the kernel of the homomorphism f.
It is denoted by Ker f or Ker (f)
Ker f = {x ∈ G | f(x) = e’}
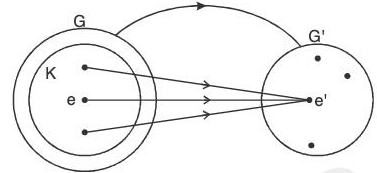
Example : The mapping f :
is a homomorphism of 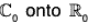 because for z1, z2 ∈
because for z1, z2 ∈ 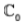
f(z1 z2) = |z1 z2| = |z1| |z2| = f(z1) f(z2)
Again Ker (f) = {z ∈ C0 | f(z) = 1}
= {z ∈ C0 ||z| = 1}
Example : The mapping f : 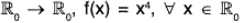 is a homomorphism on
is a homomorphism on  , because for any x1, x2 ∈
, because for any x1, x2 ∈ 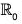
f(x1x2) = (x1x2)4 = x14.x24 = f(x1).f(x2) and
Ker(f) = {x ∈ 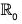 | f(x) = 1}
| f(x) = 1}
= {x ∈ 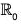 | x4 = 1} = {1 -1}
| x4 = 1} = {1 -1}
Example : The mapping f : 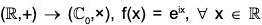
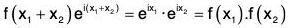
Again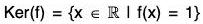
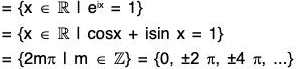
Example : If f :  f(x + iy) = x, then f is a homomorphism from to
f(x + iy) = x, then f is a homomorphism from to 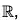 because for any (x1 + iy1), (x2 + iy2) ∈
because for any (x1 + iy1), (x2 + iy2) ∈ 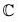
f[(x1 + iy1) + (x2 + iy2)] = f[(x1 + x2) + i(y1 + y2)]
= x1 + x2
= f(x1 + iy1) + f(x2 + iy2)
Again Ker (f) = {(x + iy) ∈ 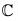 | f(x + iy) = 0}
| f(x + iy) = 0}
= {(x + iy) ∈ 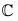 | x = 0}
| x = 0}
= the set of imaginary numbers.
Example : Let Sn be the symmetric group of degree n and G = {1, -1} multiplicative group, then the mapping f defined by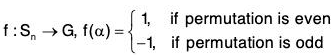
is a homomorphism of Sn onto G and Ker(f) = An
(Alternating group i.e., the set of even permutations of degree n)
Theorem : [First theorem on homomorphism]
If f is a homomorphism from a group G to G’ with kernel then  .
.
Proof : Let e and e' be the identities of G and G’ respectively
Ker(f) K = {x ∈ G | f(x) = e’} ⊂ G.
∵ f(e) = e’ ⇒ e ∈ K ⇒ K ≠ 4 φ
∵ Let a, b ∈ K; then f(a) = e’ and f(b) = e’.
Again f(ab-1) = f(a) f(b-1) [∵ f is homomorphism]
= f(a)[f(b)]-1
= e’(e’)-1 = e’e' = e’
ab-1 ∈ K
Thus we see that a ∈ K, b ∈ K ∈ ab-1 ∈ K
Therefore the Ker(f) is a subgroup of G. : Let x ∈ G and a ∈ K, then f(xax-1) = f(x).f(a) f(x-1) [∵ f is homomorphism]
: Let x ∈ G and a ∈ K, then f(xax-1) = f(x).f(a) f(x-1) [∵ f is homomorphism]
= f(x)e’[f(x)]-1 [∵ a ∈ K ⇒ f(a) = e’]
= f(x) [f(x)]-1 = e'
∴ x ∈ G, a ∈ K ⇒ xax-1 ∈ K.
Therefore 
Theorem : If f is a homomorphism of a group G onto a group and g is a homomorphism of G’ onto a group G", then gof is a monomorphism of G onto G”.
Also the kernel of f is a subgroup of that of gof.
Proof : Since f : G → G’ and g : G’ → G” are onto mappings so are composite mapping g o f : G → G” exist and it is also onto.
Again for any a, b ∈ G
(gof)(ab) = g[f(ab)]
= g[f(a) f(b)] [∵ f is homomorphism]
= g[f(a)].g[f(b)] [∵ g is homomorphism]
= (gof)(a).(gof)(b)
∴ gof is also a group homomorphism from G to G”.
If K and K’ are kernel’s of f and gof respectively, then K = {x ∈ G | f(x) = e’}, where e’ is the identity of G’
and K = {x ∈ G | (gof) (x) = e”}, where e’’ is the identity of G”
By theorem, K and K’ are subgroups of G.
K is a subgroup of K’ : Let x ∈ K.,
then x ∈ K ⇒ f(x) = e’
⇒ g[f(x)] = g(e’) = e”
⇒ (gof)(x) = e” ⇒ x ∈ K’
∴ K ⊂ K’.
which shows that K is a subgroup of K'.
Theorem : A homomorphism f defined from a group G to a group G’ is a monomorphism iff Ker f = {e}, where e is the identity of G.
Proof : (⇒) : First suppose that f is a monomorphism of G onto G and K is the kernel of f. If a ∈ K, then
a ∈ K ⇒ f(a) = e’, where e’ is the identity of G'
⇒ f(a) = f(e) [∵ f(e) = e’]
⇒ a = e [∵ f is one one]
or K = {e}
Conversely (⇐) : Suppose f is a homomorphism from G to G’ and kernel of f i.e. K = {e}. If a, b ∈ G, then
f(a) = f(b) ⇒ f(a) [f(b)]-1 = f(b)[f(b)]-1
⇒ f(a) f(b-1) = e’
⇒ f(ab-1) = e’ ⇒ ab-1 ∈ K
⇒ ab-1 = e [∵ K = {e}]
⇒ a = b
∴ f is one one mapping.
Therefore f is monomorphism ⇔ Ker f = {e}.
Theorem : Every homomorphic image of an abelian group is abelian but not conversely.
Proof. Let f be a homomorphism of an abelian group G to a group G’. By theorem, the homomorphic image f(G) of G is a subgroup of G'.
f(G) is abelian :
Let a’, b’ ∈ f(G), then there exist a, b in G such that
f(a) = a’ and f(b) = b'.
Now a’b’ = f(a) f(b)
= f(ab) [∵ f is homomorphism]
= f(ba) [∵ G is commutative]
= f(b) f(a)
= b’ a'
Thus a’, b’ ∈ f(G) ⇒ a’ b’ = b’ a’
∴ f(G) is also an abelian group.
Conversely (⇐) : The converse is not necessarily true as can be seen from the following example :
f : S3 → {1,-1}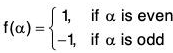
is a homomorphism of S3 onto {1, -1}
Moreover the multiplicative group f(S3) = {1, -1} is abelian cyclic, but S3 is neither abelian not cyclic.
Theorem : Every homomorphic image of a cyclic group is cyclic but not conversely.
Proof : Let f be a homomorphism of a cyclic group G = [a] to a group G\ By theorem f(G) is a subgroup of G’.
f(G) is cyclic :
Let x ∈ f(G), then x = f(an), where n ∈ Z
Again f(an) = f(aaa.... (n times))
= f(a) f(a)...f(a) (n times) [∵ f is homomorphism]
= [f(a)]n
which shows that every element of f(G) is some integral power of f(a)
i.e. f(G) = [f(a)]
Hence f(G) is also a cyclic group.
Conversely (⇐) : The converse is not necessarily true as can be seen from the following example :
f :S3 → {1,-1}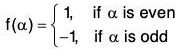
is a homomorphism of S3 onto {1, -1}
Moreover the multiplicative group f(S3) = {1, -1} is abelian cyclic, but S3 is neither abelian nor cyclic.
Natural morphism : Definition :
Let 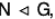 , then f : G → G/N s.t. f(x) = Nx, ∀ x ∈ G is called a natural morphism of canonical mapping or projection mapping of G onto G/N.
, then f : G → G/N s.t. f(x) = Nx, ∀ x ∈ G is called a natural morphism of canonical mapping or projection mapping of G onto G/N.
Theorem : Every group is homomorphic to its quotient group.
Proof : Let N be a normal subgroup of a group G.
Consider a mapping p from G to G/K defined as :
p : G → G/N, p(x) = Nx, ∀ x ∈ G.
We see that Na ∈ (G/N), there exists a e G such that p(a) = Na
∴ p is onto.
Again for any a, b ∈ G
p(ab) = Nab = NaNb = p(a) p(b).
∴ p is a epimorphism of G onto G/N.
Corollary. If p is a homomorphism of G onto G/N defined as above, then Ker p = N.
Proof : As proved above, the mapping p : G → G/N, p(x) = Nx, ∀ x ∈ G is a homomorphism of G onto G/N. Let Ker (p) = K, then K = {x ∈ G | p(x) = N} [N is the identity in G/N]
K = N :
If x ∈ K ⇒ px = N
⇒ Nx = N ⇒ x ∈ N
∴ K ⊂ N ...(1)
Again, if x ∈ N ⇒ p(x) = Nx
⇒ p(x) = N [∵ x ∈ N ⇒ Nx = N]
⇒ x ∈ K
N ⊂ K ...(2)
(1) and (2) ⇒ K = N.
Theorem : Let f : G → G’ be a morphism of groups. Let ⊂ K, the kernel of f; then there exists a unique morphism
⊂ K, the kernel of f; then there exists a unique morphism
φ : G/N → G' such that f = φ o p
Proof : Let Ker f = K = N, therefore N ⊂ L ...(1)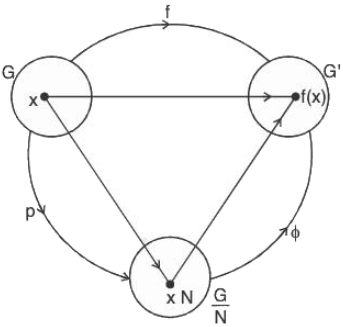 Let p be a canonical map defined by
Let p be a canonical map defined by
p : G → G/N, p(x) = xN. ...(2)
Let φ : G/N → G', φ(xN) = f(x) ...(3)
φ is well defined :
∵ x1 N = x2 N ⇒ x2-1 x1 ∈ N ⊂ K
⇒ f(x2-1x1) = e' [e' ∈ G']
⇒ f(x2-1)f(x1) = e'
⇒ f(x1) = f(x2)
⇒ f(x1N) = f(x2N)
Therefore φ is well defined,
and (φ o p)x = φ[p(x)] x ∈ G
= φ(xN) = f(x)
∴ f = φ o p
φ is a morphism :
f(x1 Nx2 N) = f(x1 x2 N)
= f(x1 x2)
= f(x1) f(x2)
= φ(x1 N)φ(x2 N)
∴ φ is a morphism.
Corollary : Ker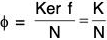
Proof : Let x ∈ K then φ(x N) = f(x) = e’
∴ x N ∈ Ker φ
⇒ (K/N) ⊂ Ker φ ...(i)
and x N ∈ Ker φ ⇒ f(x N) = e'
⇒ f(x) = e’
⇒ x ∈ Ker f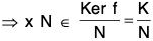
⇒ Kerφ ⊂ K/N ...(ii)
(i) and (ii) ⇒ Ker f = 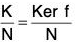
Corollary : Image φ = Image f
Proof : x ∈ Image φ ⇒ x = f(g), g ∈ G
⇒ Image φ ⊂ Image f
and f(g) = φ(g N)
Image φ = Image f
Theorem : Every homomorphic image of a group G is isomorphic to some quotient group of G.
Proof: Let G’ be a homomorphic image of a group G and f be the corresponding onto morphism from G onto G'.
If K is the kernel of f, then 
Hence G/K is a quotient group of G.
To prove that G / K = G'.:
Define a map φ from G/K to G’ as follows :
φ : G/K → G', f(Kx) = f(x), x ∈ G.
φ is well defined :
i.e., Ka = Kb ⇒ φ(Ka) = φ(Kb), a, b ∈ G
We see that Ka = Kb ⇒ ab-1 ∈ K
⇒ f(ab-1) = e', where e' is identity in G’
⇒ f(a) f(b-1) = f(a) [f(b)]-1 = e’
⇒ f(a) = f(b)
⇒ f(Ka) = φ(Kb)
∴ φ is a well defined mapping.
Again φ(Ka) = f(Kb) ⇒ f(a) = f(b)
⇒ f(a) [f(b)]-1 = f(b) [f(b)]-1 = e
⇒ f(a) f(b)-1 = e’
⇒ f(ab-1) = e’
⇒ ab-1 ∈ K [∵ K is the kernel of f]
⇒ Ka = Kb [∵ Ka = Kb ⇔ ab-1 ∈ K]
∴ φ is one one.
φ is onto :
Lastly, if a ∈ G’ then a ∈ G such that
f(a) = a’ [∵ f is onto]
Hence Ka ∈ G/K such that
ψ(Ka) = f(a) = a’
∴ φ is onto
φ is a homomorphism : Now for any Ka, Kb ∈ G/K
φ[Ka Kb] = φ [Kab] = f(ab) = f(a) f(b) = φ(Ka) φ(Kb)
∴ φ is a morphism from G/K to G.
Therefore φ is an isomorphism from G/K to G’.
Hence G/K ≅ G’.
Example : If Sn be the symmetric group of degree n and G = [{1, -1}, x], then show that the mapping f : Sn → G defined by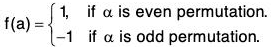
is a homomorphism of Sn onto G. Also find its kernel.
Let α, β ∈ Sn. Here four cases arise :
Case 1. When α, β will also be an even permutation :
In this case αβ will also be an even permutation.
Therefore f(αβ) = 1 =1.1 = f(α).f(β)
Case 2. When α, β both are odd permutations :
In this case αβ will be an even permutation.
Therefore f(αβ) = 1 = (-1).(-1) = f(α).f(β)
Case 3. When is α even and β is odd permutation :
In this case αβ will be an odd permutation.
Therefore f(αβ) = -1 = 1.(-1) = f(α).f(β)
Case 4. When α is odd and β is even permutation :
In this case αβ will be an odd permutation.
Therefore f(αβ) = -1 = (-1).1 = f(α).f(β)
Thus we see that f(αβ) = f(α).f(β) ∀ α, β ∈ Sn
Therefore f is a morphism from Sn to G.
By definition, Ker(f) = {α ∈ Sn | f(α) = 1}
= {α ∈ Sn | (α) is even permutation}
= group of even permutations of degree n.
= An.
Example : If 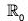 denote the multiplicative group of non-zero real numbers, then show that the mapping
denote the multiplicative group of non-zero real numbers, then show that the mapping 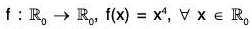 is a homomorphism in
is a homomorphism in 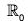 . Also find its kernel.
. Also find its kernel.
Let x1, x2 ∈
. then
f(x1x2) = (x1x2)4 = x14x24 = f(x1).f(x2)
∴ f is a morphism in
Again kernel of
or ker f = {1, -1}
Example : If f is a homomorphism of a group G to G’ with kernel K and a ∈ G, a' ∈ G’ are such that f(a) = a’; then prove that the set of those elements of G which are mapped to a’ is the coset Ka of K in a
We have to prove that f-1(a’) = {x ∈ G | f(a) = a’} = Ka
Let e and e’ be the identities of G and G’ respectively,
Let y ∈ f-1(a’) then f(y) = a’ and
f(ya-1) = f(y) f(a-1)
= a’[f(a)]-1
= a’(a’)-1 = e’
∴ ya-1 ∈ K ⇒ y ∈ Ka
Thus y ∈ f-1(a’) ⇒ y ∈ Ka ⇒ f-1(a’) ⊂ Ka ...(1)
Again, let x ∈ Ka, then
x ∈ Ka ⇒ x = ka where k is any element of K
⇒ f(x) = f(ka) = f(k) f(a) = e’a’ = a’
⇒ x ∈ f-1(a’)
∴ Ka ⊂ f-1(a’) ...(2)
(1) and (2) ⇒ f-1(a’) = Ka.
Example : If f is a homomorphism of a group G to Gr with kernel K then prove that for any a, b ∈ G;
f(a) = f(b) ⇔ ab-1 ∈ K
For any a, b ∈ G
f(a) = f(b) ⇔ f(a)[f(b)]-1 = f(b)[f(b)]-1 = e' where e’ is the identity of G
⇔ f(a) f(b-1) = e’
⇔ f(ab-1) = e’ [∵ f is a morphism]
⇔ ab-1 ∈ K
A homomorphism φ from a group G to a group 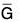 is a mapping from G into
is a mapping from G into 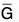 that preserves the group operation; that is, φ(ab) = φ(a)φ(b) for all a, b in G.
that preserves the group operation; that is, φ(ab) = φ(a)φ(b) for all a, b in G.
Kernel of a Homomorphism
The kernel of a homomorphism φ from a group G to a group with identity e is the set {x ∈ G | φ(x) = e}. The kernel of φ is denoted by Ker φ.
Example : Any isomorphism is a homomorphism that is also onto and one-to-one. The kernel of an isomorphism is the identity.
Example : Let G = GL(2, 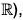 and let
and let 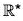 be the group of non-zero real number under multiplication. Then the determinant mapping A → det A is a homomorphism from G to
be the group of non-zero real number under multiplication. Then the determinant mapping A → det A is a homomorphism from G to 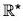 . The kernel of the determinant mapping is SL(2,
. The kernel of the determinant mapping is SL(2, 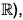 .
.
where
GL(2, R) : is the group of non-singular real-valued matrices under multiplication. It contains all non- singular transformations, including expansions or contractions, reflections, and translations.
SL(2, R) : is the group of determinant 1 real-valued matrices under multiplication. Since the determinant of a product is the product of the determinants, this is a closed group. It contains all rotations without any reflections. This is all rotation-translations, and it preserves
Also OL(2, R) : is the group of orthogonal matrices, whose transposes are also their inverses. Obviously their determinant will be +1 (As det(A)2 = det(A)det(AT) = det(AAT) = det(AA-1) = det(ld) = 1).
Also SOL(2, R) : is the group of special orthogonal matrices, whose transposes are also their inverses and determinant is +1. It is the group of rotation matrices or equivalently, the unit circle.
Properties of Homomorphisms
Theorem : Properties of Elements under Homomorphism’s
Let φ be a homomorphism from a group G to a group 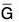 and let g be an element of G. Then
and let g be an element of G. Then
- φ carries the identity of G to the identity of
 .
. - φ(gn) = (φ(g))n.
- If |g| = n, then |φ(g)| divides n.
- If φ(g) = g', then φ-1(g') = {x ∈ G | φ(x) = g’} = gKer φ.
Theorem : Properties of Subgroups under Homomorphism
Let be a homomorphism from a group G to a group 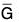 and let H be a subgroup of G. Then
and let H be a subgroup of G. Then
- φ(H) = {φ(h) | h ∈ H} is a subgroup of
 .
. - If H is cyclic, then φ(H) is cyclic.
- If H is Abelian, then φ(H) is Abelian.
- If H is normal in G, then φ(H) is normal in φ(G).
- If |Ker φ| = n, then φ is an n-to-1 mapping from G onto φ(G).
- If |H| = n, then lφ(H)| divides n.
- If
 is a subgroup of
is a subgroup of  , then φ-1(
, then φ-1( ) = {k ∈ G | φ(k) ∈
) = {k ∈ G | φ(k) ∈  } is a subgroup of G.
} is a subgroup of G. - If
 is a normal subgroup of
is a normal subgroup of  then φ-1(
then φ-1( ) = {k ∈ G | φ(k) ∈
) = {k ∈ G | φ(k) ∈  } is a normal subgroup of G.
} is a normal subgroup of G. - If φ is onto and Ker φ = {e}, then φ is an isomorphism from G to
 .
.
Kernels Are Normal
Let φ be a group homomorphism from G to 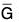 . Then Ker φ is a normal subgroup of G.
. Then Ker φ is a normal subgroup of G.
The First Isomorphism Theorem
Theorem : Frist Isomorphism Theorem
Let φ be a group homomorphism from G to 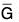 . Then, the mapping from G/Ker φ to φ(G), given by φKer φ → φ(g), is an isomorphism. In symbols, G/Ker φ ≈ φ(G).
. Then, the mapping from G/Ker φ to φ(G), given by φKer φ → φ(g), is an isomorphism. In symbols, G/Ker φ ≈ φ(G).
Proof : Let us use ψ to denote the correspondence gKer φ → φ(g). First, we show that ψ is well defined (that is, the correspondence is independent of the particular coset representative chosen). Suppose xKer φ = yKer φ. Then y-1x ∈ Ker φ and e = φ(y-1x) = (φ(y))-1φ(x). Thus φ(x) = φ(y), and ψ is indeed a function. To show that y is operation-preserving, observe that ψ(xKer φ yKer φ) = ψ(xyKer φ) = φ(xy) = φ(x)φ(y) = ψ(xKer φ)ψ(yKer φ). Finally, if ψ(g1 Ker φ) = ψ (g2Ker φ), then φ(g1) = φ(g2), so that g2-1g1, ∈ Ker φ. It follows that ψ is one -to -one.
Example : 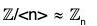
Consider the mapping from 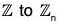 defined in Example. Clearly, its kernel is <n>. So, by First Isomorphism Theorem
defined in Example. Clearly, its kernel is <n>. So, by First Isomorphism Theorem 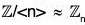 .
.
Theorem : Normal Subgroup Are Kernels
Every normal subgroup of a group G is the kernel of a homomorphism of G. In particular, a normal subgroup N is the kernel of the mapping g → gN from G to G/N.Proof: Define φ:G → G/N by φ(g) = gN. (This mapping is called the natural homomorphism from G to G/N.) Then, φ(xy) = x(xy)N = xNyN = <φ(x)φ(y).
Isomorphism : Definition :
A morphism f of a group (G, *) to a group (G', o) is an isomorphism if
- f is one-one i.e., f(a) = f(b) ⇒ a = b, f is a morphism i.e., f(a*b) = f(a) o f(b), V a,b e G a, b ∈ G
- f is onto i.e, f(G) = G’
- f is a morphism i.e., f(a*b) = f(a) o f(b), ∀ a, b ∈ G
From the above definition, it is clear that a group morphism is an isomorphism if f is a bijection.
Isomorphic Groups
A group G is said to be isomorphic to a group G \ if there exists an isomorphism of G onto G’. Symbolically, we write it as G ≅ G’.
Examples of Isomorphism
Example : For every group G, the identity mapping lG defined by
lG: G → G, lG(x) = x, ∀ x ∈ G
is an isomorphism of G onto itself, because lG is clearly one-one onto and for a, b ∈ G, lG(ab) = ab = lG(a) lG(b)
Example : The map f : 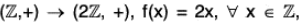 is an isomorphism from Z onto 2
is an isomorphism from Z onto 2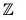 , because for any x1, x2 ∈
, because for any x1, x2 ∈ 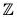
- f(x1 + x2) = 2(x1 + x2) = 2x1 + 2x2 = f(x1) + f(x2)
∴ f is a group morphism. - f(x1) = f(x2) ⇒ 2x1 = 2x2 ⇒ x1 = x2
∴ f is one-one. - f(Z) = 2
 ∴ f is onto.
∴ f is onto.
Hence Z ≅ 2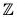 .
.
Example : The map f : 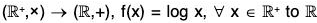 is an isomorphism, because for x1, x2 ∈
is an isomorphism, because for x1, x2 ∈ 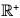
- f(x1 x2) = log(x1 x2) = log x1 + log x2 = f(x1) + f(x2)
- f(x1) = f(x2) ⇒ log x1 = log x2 ⇒ x1 = x2
- f(R+) = R
Properties of Isomorphism
Theorem : A homomorphism f defined from a group G onto G’ is an isomorphism iff Ker(f) = {e}.
Proof : (⇒): Suppose f is an isomorphism of G onto G’ and K is the kernel of f. If a ∈ G, then
a ∈ K ⇒ f(a) = e’, where e’ is the identity of G
⇒ f(a) = f(e) [∵ f(e) = e’]
⇒ a = e [∵ f is one-one]
This shows that K contains only the identity e i.e., ∴ K = {e}
Conversely (⇐) : Suppose that K = {e}.
Let a, b ∈ G, then
f(a) = f(b) ⇒ f(a) [f(b)]-1 = f(b)[f(b)]-1
⇒ f(a) f(b-1) = e’ ⇒ f(ab-1) = e’
⇒ ab-1 ∈ K
⇒ ab-1 = e [∵ K = {e}]
⇒ a = b
∴ f is bijective homomorphism.
Hence it is an isomorphism.
Theorem : The relation of isomorphism '≅' in the set of group is an equivalence relation.
Proof : (i) Reflexive : For any group G, the identity mapping lG defined by lG(x) = x is an isomorphism because lG is a bijection and for any a, b ∈ G, lG(ab) = ab = lG(a) lG(b)
∴ G ≅ G
⇒ relation ≅ is reflexive.
(ii) Symmetric : Let G and G’ be two groups such that G ≅ G and let f be the corresponding isomorphism. Since by definition f is a bijection, so its inverse f-1 : G' → G exists and it is also a bijection.
Further if a, b ∈ G and a', b’ ∈ G’ such that
f(a) = a’ and f(b) = b'.
then a = f-1 (a’) and b = f-1 (b’)
then f-1 (a’b’) = f-1 [f(a) f(b)] [by (1)]
= f-1 [f(ab)]
= ab
= f-1(a’) f-1(b’)
Therefore f-1 is an isomorphism from G' onto G.
Hence G’ ≅ G.
∴ G ≅ G’ ⇒ G' ≅ G
Therefore the relation ≅ is symmetric.
(iii) Transitive : Let G, G’ and G” be three groups such that
G ≅ G’ and G’ ≅ G”
Also let f and g be their respective isomorphism. Since by definition f and g are bijections, so gof : G → G” is also a bijection. Further, gof is a homomorphism of G to G”. Hence gof is an isomorphism from G to G”.
∴ G ≅ G”
Therefore the relation ≅ is transitive.
From the above discussion, the relation of isomorphism '≅’ is an equivalence relation.
Remark : The relation of isomorphism ≅ in a family of groups being an equivalence relation, partitions that family into disjoint equivalence classes. If G ≅ G’ i.e., if G and G’ belong to the same equivalence class, then we simply say that G and G’ are isomorphic. When two groups are isomorphic, then their structures will be basically identical. In such a case, we sometimes say that two groups are abstractly identical.
Theorem : Cayley Theorem :
Every group is isomorphic to some permutation group or G ≅ PA.
Proof : Let G be a group. Corresponding to every a in G, we define a map fa as follows :
fa(x) = ax, ∀ x ∈ G
∵ a ∈ G, x ∈ G ⇒ ax ∈ G
∴ fa : G → G is a function
Further for any x, y ∈ G
fa(x) = fa(y) ⇒ ax = ay
⇒ x = y [by cancellation law in G]
∴ f is one-one and for every x ∈ G, there exists a-1x ∈ G such that fa(a-1 x) = a(a-1 x) = (aa-1)x = x
∴ fa is onto.
As such fa is a one one mapping of G onto G itself.
Hence fa is a permutation of G.
Let SG be the group of all permutations of G.
Let us now consider the mapping φ from G to SG, defined by φ : G → SG, φ(x) = fx, ∀ x ∈ G.
Now for any x, y ∈ G
φ(xy) = fxy = fxfy = φ(x) φ(y)
∴ φ is a homomorphism from a group G onto SG.
Consequently φ(G) = G’ is a subgroup of the permutation group SG and φ is an epimorphism from G onto G’.
Also for any a, b ∈ G
φ(a) = φ(b) ⇒ fa = fb
⇒ fa(x) = fb(x), ∀ x ∈ G
⇒ ax = bx ⇒ a = b
∴ φ is one-one.
Hence φ is an isomorphism from a group G onto permutation group G'. Consequently, G ≅ G’.
Theorem : Every infinite cyclic group is isomorphic to the additive group of integers i.e. 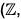 +).
+).
Proof. Let G = [a] be an infinite cyclic group generated by a.
First we show that no two distinct integral powers of a can be equal.
For if possible, let ai = aj where i, j ∈ 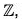 i > j, then
i > j, then
ai = aj ⇒ ai a-j = aj a-j
⇒ ai-j = a0 = e
⇒ O(a) is finite.
⇒ G is finite which is a contradiction.
∴ G = {...a-3, a-2, a-1, a0 = e, a, a2, a3,...} has all distinct elements.
Consider the mapping f from the group G to the group 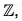 defined as
defined as
f : G → Z, f(an) = n, ∀ an ∈ G
We see that for any am, an ∈ G
am ≠ an ⇒ m ≠ n ⇒ f(am) ≠ f(an)
∴ f is one-one
and for any n ∈ 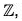 , there exists a" such that f(an) = n
, there exists a" such that f(an) = n
∴ f is onto.
Again, f(am an) = f(am+n) = m + n = f(am) + f(an)
∴ f is a homomorphism from the group G to Z
Hence f is an isomorphism of G onto 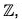 which proves thatG ≅
which proves thatG ≅ 
Remark. Since the relation of isomorphism is an equivalence relation, so with the help of theorem, we conclude that any two infinite cyclic groups are isomorphic to each other. Hence we can say that there exists one and only one infinite cyclic group.
Example : If m is a fixed integer then show that the following mapping f is an isomorphism from 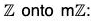
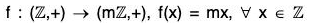
For any x1 x2 ∈
f(x1) = f(x2) ⇒ mx1 = mx2 ⇒ x1 = x2
∴ f is one-one and for any mx ∈ mZ there exists x ∈ Z such that
f(x) = mx
∴ f is onto.
Again f(x1 + x2) = m(x1 + x2) = mx1 + mx2 = f(x1) + (x2)
∴ f is homomorphism
Thus we see that f is a homomorphism from the grouponto m
which is bijective.
Consequently,
Example : Show that the additive group  of real numbers is isomorphic to the multiplicative group
of real numbers is isomorphic to the multiplicative group 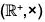 of positive real numbers.
of positive real numbers.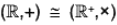
Consider the mapping f from the group
to group
defined as
We know that for any x1, x2 ∈
∴ f is one-one.
and for everythere exist log
such that
f(log x) = elog x = x
∴ f is onto.
Again, f(x1 + x2) =
∴ f is homomorphism.
As such f is a homomorphism from the groupto the group
which is bijection. Hence f is an isomorphism.
Consequently
Example : Prove that the following groups are isomorphic groups :
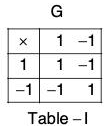
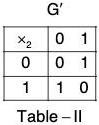
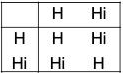
(a) ({1, - 1}, x ) and ({0, 1}, +2)
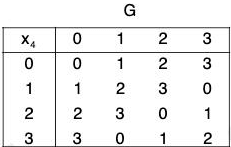
(b) ({0, 1, 2, 3},+4) and ({1, 2, 3, 4}, x5)
(a) Let G = {1, -1} and G’ = {0, 1}
Define a map f from G to G' as f(1) = 0, f(-1) = 1.
Clearly f is bijection.
The composition table of both the groups G and G’ are as below :

In table II, if we replace 0 by 1 and 1 by -1, then the two tables become identical. This show that f preserves composition and is a bijection.
Therefore f is isomorphism.
Hence G ≅ G’
(b) Let G = {0, 1, 2, 3} and G’ = {1, 2, 3, 4}
Define a map f from G to G’ as
f(0) = 1, f(1) = 2, f(2) = 3 and f(3) = 4
Clearly f is bijection. The composition table of both the groups are :Replacing 1, 2, 4, 3 by 0, 1, 2, 3 respectively in the table II, the two tables become identical.
This shows that f preserves composition and is a bijection.
Therefore f is isomorphism.
Hence G ≅ G’
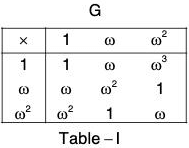
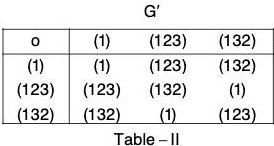
Example : Prove that the following group of permutations (G’) are isomorphic to multiplicative group G = {1, ω, ω2}.
(a) G’ = ({(1), (123), (132)}, o)
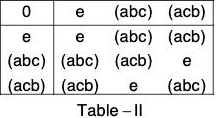
(b) G’ = ({e, (abc), (acd)}, o)
(a) Let G {1, ω, ω2} and G’ = {(1),(123),(132)}
Define a mapping f from G to G’ as follows :
f(1) = (1), f(ω) = (123) and f(ω2) = (132).
Clearly f is bijection. The composition table of both the groups are:
Replacing (1), (123), (132) by 1, ω and ω2 respectively in the table II, the two tables become identical.
This shows that f preserves composition and is a bijection.
Therefore f is isomorphism.
Hence G ≅ G’
(b) Define a mapping f from G to G’ as follows :
f(1) = e, f(ω) = (abc) and f(ω2) = (acb)
Clearly, f is bijection. The composition table of the group G’ is :
Replacing e, (abc) and (acb) by 1, ω and ω2 respectively in the above table of G \ the two tables of group G and G\ the two tables of group G and G’ become identical. This show that f preserves composition and is a bijection.
Therefore f is isomorphism.
Hence G ≅ G'
Example : Find the permutation group isomorphic to the group ({1, -1, i, -i} ,x)
Let G = {1, -1, i, -i}. Define a map f for a ∈ G as
fa : G → G, fa(x) = ax, ∀ x ∈ G
Then we shall have
Hence by Cayley’s theorem, the permutation group isomorphic to G is G' = {f1, f(-1), f(i), f(-i)}
It can be easily seen that the corresponding isomorphism φ is defined as φ(x) = fx, ∀ x ∈ G.
Note. The group G’ is generally known as the Regular permutation group isomorphic to the group G.
Example : Prove that a finite cyclic group of order n is isomorphic to the additive group of residue classes modulo n.
Solution : Let G = [a] = {a, a2, a3 ..., an = e} be a cyclic group of order n. Let G ’ be the additive group of residue classes modulo n. Then G’ = {[0], [1], [2],...,[n - 1]}
Define a map f : G → G’.f(ar) = [r], ∀ ar ∈ G
Clearly f(an) = [n] = [0]. We see that for any ar, as ∈ S
f(ar) = f(as) ⇒ [r] = [s] ⇒ r = s ⇒ ar = as
∴ f is one one.
and O(G) = n = O(G’) and f is one-one ⇒ f is onto
Again f(ar.as) = f(ar+s) = [r + s] = [r] + [s] = f(ar) + f(as).
Therefore f is an isomorphism from G to G'.
Hence G ≅ G’.
Automorphism
An isomorphic mapping of a group G onto G itself is called an automorphism of G.It is denoted by AG or Aut (G)
A mapping f : G → G is called automorphism of G if
(i) f is a bijection
and (ii) f(ab) = f(a) f(b), ∀ a, b ∈ G
Example : The identity mapping lG is an automorphism on G because lG is a bijection and lG(ab) = ab = lG (a) lG (b), ∀ a, b ∈ G
Example : The mapping f : (C, +) → (C, +), f(z) = 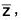 ∀ z ∈ G is an automorphism on C because for any z1, z2 ∈ C
∀ z ∈ G is an automorphism on C because for any z1, z2 ∈ C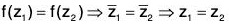
∴ f is one-one.
and for every z ∈ C there exists 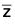 ∈ C such that f(
∈ C such that f(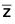 ) = (
) = (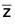 ) = z
) = z
∴ f is onto
Again 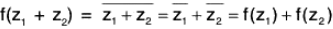
Therefore f is an isomorphism on the group C
i.e., this is an automorphism on the group C.
Theorem : The set AG of all automorphisms of a group G with composite of functions as binary operation is a group.
Proof : Let AG be the set of all automorphisms on G and f, g ∈ AG,
then f, g ∈ AG ⇒ f and g are one-one mappings of G onto itself
⇒ gof is also a one-one mapping of G onto itself.
Further if a, b ∈ G, then
(gof)(ab) = g[f(ab)]
= g[f(a) f(b)] [∵ f is automorphism]
= g[f(a)] g[f(b)] [∵ g is automorphism]
= (gof)(a)(gof)(b)
∴ gof is an automorphism of G.
Therefore f ∈ AG, g ∈ AG ⇒ gof ∈ AG
i.e., AG is closed for the operation of composite of functions.
Verification of Group axioms in AG :
[G1] Since the composite of mappings is always is always associative, so this is also associative in AG i.e., (fog)oh = fo(goh), ∀ f, g, h ∈ AG.
[G2] Since the identity mapping lG of G is an automorphism such that for every f ∈ AG, lG of = f = f o lG
∴ lG is the identity element of AG
[G3] Let f ∈ AG, then
f ∈ AG ⇒ f is a bijection on G.
Again, for any a, b ∈ G, let
f-1(a) = a1 and f-1(b) = b1 ∀ a1, b1 ∈ G.
⇒ a = f(a1) and b = f(b1)
Now f-1 (ab) = f-1 [f(a1) f(b1)]
= f-1 [f(a1 b1)] [∵ f is automorphism]
= a1 b1 = f-1 (a) f-1 (b)
∴ f-1 is also an automorphism of G.
Hence f-1 ∈ AG, Thus the inverse for each f exists in AG.
From the above discussion, AG is also a group for the composite of functions.
Example : If a be an element of a group G, then the mapping fa : G → G, fa(x) = axa-1, ∀ a ∈ G is an automorphism of g.
Let x1, x2 ∈ G, then
fB(x1) = fa(x2) ⇒ aax1a-1 = ax2a-1
⇒ x1 = x2 [by cancellation law]
∴ fa is one-one.
Again for every x ∈ G, there exists a-1 xa ∈ G such that
fa(a-1 xa) = a(a-1 xa)a-1 = (aa-1)x(aa-1) = exe = x.
∴ fa is onto.
Lastly, we see that for any x1, x2 ∈ G
fa(x1 x2) = a(x1 x2)a-1
= (ax1 a-1)(ax2 a-1) = fa(x1) fa(x2)
∴ fa is an automorphism on the group G.
Remark : The above automorphism fa is called the Inner automorphism of the group G determined by a.
Example : In a group G, show that, the mapping f : G → G, defined by f(x) = x-1, ∀ x ∈ G is an automorphism iff G is abelian.
(⇒) Suppose that G is an abelian group and a, b ∈ G. Then
f(a) = f(b) ⇒ a-1 = b-1 (a-1)-1 = (b-1)-1 ⇒ a = b.
∴ f is one-one and for every a ∈ G there exists a-1 ∈ G such that
f(a-1) = (a-1)-1 = a.
∴ f is onto.
Again, f(ab) = (ab)-1 = b-1 a-1 = a-1 b-1 [∵ G is cumulative]
= f(a) f(b).
∴ f is an isomorphism on G i.e., this is an automorphism on G.
Conversely (⇐) : Suppose that f is an automorphism of G, then for any a, b ∈ G,
f(ab) = (ab)-1 [by definition of f]
= b-1 a-1 = f(b) f(a)
= f(ba) [∵ f is an automorphism]
Now, since f is one-one, therefore
f(ab) = f(ba) ⇒ ab = ba
⇒ G is an abelian group.
FACTOR GROUPS
We have already seen that if 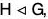 , then every left (right) coset of H is equal to its corresponding right (left) coset in G. Again the product of any two right (left) cosets of H is also a right (left) coset of H. This leads to a natural definition of a binary composition in the set of all cosets of H in G. As such the set of all left cosets of H coincide with the set of all right cosets of H. In the next theorem, we shall prove that this set is a group for the natural binary composition. This group is called the Quotient group or Factor group of G by H and is denoted by G/H.
, then every left (right) coset of H is equal to its corresponding right (left) coset in G. Again the product of any two right (left) cosets of H is also a right (left) coset of H. This leads to a natural definition of a binary composition in the set of all cosets of H in G. As such the set of all left cosets of H coincide with the set of all right cosets of H. In the next theorem, we shall prove that this set is a group for the natural binary composition. This group is called the Quotient group or Factor group of G by H and is denoted by G/H.
Theorem : The set of all cosets of 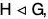 is a group with respect to multiplication of cosets defined as follows :
is a group with respect to multiplication of cosets defined as follows :
Ha Hb = Hab, a b ∈ G
Proof : Binary composition is well defined :
Let G/H be the set of all cosets of H in G.
i.e. G/H = {Ha | a ∈ G} = {aH | a ∈ G}.
∵ a ∈ G, b ∈ G ⇒ ab ∈ G ⇒ Hab ∈ G/H.
∴ Ha ∈ G/H, Hb ∈ G/H ⇒ HaHb = Hab ∈ G/H.
Therefore G/H is closed for the defined binary operation.
Verification of group axioms in G/H :
G1 : Let Ha, Hb, Hc ∈ G/H; a, b, c ∈ G, then
(HaHb)Hc = HabHc = H(ab)c
= Ha(bc) [by associativity in G]
= Ha Hbc = Ha(HbHc)
∴ the composition is associative in G/H.
G2 : H = He ∈ G/H is the identity element because for Ha ∈ G/H
HaHe = Hae = Ha
and HeH = Hea = Ha
G3 : We see that
Ha ∈ G/H ⇒ Ha-1 ∈ G/H [∵ a ∈ G ⇒ a-1 ∈ G]
and HaHa-1 = Haa-1 = He = H
Ha-1 Ha = Ha-1 a = He = H
∴ Ha-1 is the inverse of Ha in G/H.
Thus every element of G/H is invertible.
Therefore G/H is a group for the defined composition.
On the basis of the above theorem, the quotient group may also be defined as follows :
Quotient group
Let G be a group and 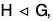 then the set G/H of all cosets of H in G together with the binary composition defined by
then the set G/H of all cosets of H in G together with the binary composition defined by
HaHb = Hab, where Ha ∈ G/H, Hb ∈ G/H is a group, and is called the quotient group of G by H.
Remarks :
- If the composition in the group is addition (+), then the composition in G/H is defined as (H + a) + (H + b) = H + (a + b).
- For the existence of the quotient group G/H, it is necessary that H is a normal subgroup of G.
Theorem : If N is a normal subgroup of a finite group G, then :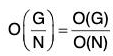
Proof : By definition,
O(G/N) = the number of different right (left) cosets of N in G.
= the index of N is G
= No. of elements in G/No. of elements in N [by Lagrange’s theorem]
= O(G)/O(N)
Properties of Quotient group
Theorem : Every quotient group of an abelian group is abelian but not conversely.
Proof : Let H be a normal subgroup of an abelian group G and a ∈ G, b ∈ G, then
a ∈ G, b ∈ G ⇒ Ha ∈ G/H, Hb ∈ G/H
∵ HaHb = Hab
= Hba [∵ G is commutative ⇒ ab = ba]
= HbHa
Thus, we see that
Ha ∈ G/H, Hb ∈ G/H ⇒ HaHb = HbHa
∴ G/H is also commutative.
Conversity (⇐) : The converse is not necessarily true.
For example : S3/A3 is an abelian group, while S3 is a non abelian group. The order of group S3/ A3 is 2 and every group of order 2 is an abelian.
Theorem : Every quotient group of a cyclic group is cyclic but not conversely.
Proof : Let H be a normal subgroup of any cyclic group G = [a].
Since every element of G is of the form an, n ∈ Z
therefore let Han ∈ G/H then
Han = H(a.a...(n times))
= HaHa...Ha (n times) [∵ Hab = HaHb]
= (Ha)n
∴ G/H = [Ha]
Therefore G/H is also a cyclic group whose generator is Ha.
Conversely : The converse is not necessarily true.
For example : S3/A3, being a group of order 2, necessarily cyclic but S3 is not cyclic group.
Example : Find the quotient group G/H and also prepare its operation table when :
G = ({1, -1, i, -i},*)
H = ({1, -1}, *)
Since G is a commutative group, therefore
Consequently, G/H exist having the following cosets of H:
H.1 ={1.1, -1.1} = {1,-1} = H
H(-1) = {1.(-1), -1 -(-1)} = {-1.1} = H
H.i. ={1.i, -1, i} = {i, -i] = Hi
H(-i) = {1 -(-i), -1 (-i))} = (-1, i} = Hi
Thus we see that G/H = {H, Hi}
The composition table of G/H is as follows :
Example : Find the quotient group G/H and also prepare its operation table when G = 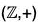 , H =
, H = 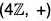
Since 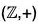 is a commutative group, therefore
is a commutative group, therefore 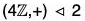
Hence G/H exists.
The cosets of H in G are as follows :
0+ H = H + 0 = {..., -8, -4, 0, 4, 8, ...} = H
1 + H = H + 1 = {..., -7, -3, 1, 5, 9, ...}
2 + H = H + 2 = {..., -6, -2, 2, 6, 10, ...}
3 + H = H + 3 = {..., -5, -1, 3, 7, 11, ...}
We further observe that
H = H + 4 = H + 8 = H + 12 = ... = H + (-4) = H + (-8) = ...
H + 1 = H + 5 = H + 9 = H + 13 = ... = H + (-3) = H + (-7) = ...
H + 2 = H + 6 = H + 10 = H + 14 = ... = H + (-2) = H + (-6) = ...
H + 3 = H + 7 = H + 11 = H + 15 = ... = H + (-1) = H + (-5) = ...
Thus H has four distinct cosets and so
G/H = {H, H + 1, H + 2, H + 3}
The composition table of G/H is as shown below :
When the subgroup H of G is normal, then the set of left (or right) cosets of H in G is itself a group-called the factor group of G by H (or the quotient group of G by H).
Theorem : Factor Group
Let G be a group and H a normal subgroup of G. The set G/H = {aH | a ∈ G} is a group under the operation (aH)(bH) = abH.
Proof : Our first task is to show that the operation is well defined; that is, we must show that the correspondence defined above from G/H x g/H into G/H is actually a function. To do this, assume that aH = a’H and bH = b’H. Then a’ = ah1 and b’ = bh2 for some h1, h2 in H, and therefore a’b’H = ah1bh2H = ah1bH = ah1Hb = aHb = abH , eH = H is the identity; a-1 H is the inverse of aH; and (aHbH)cH = (ab)HcH = (ab)cH = a(bc)H = aH(bc)H = aH(bHcH). This proves that G/H is a group.
Example : Let G = 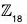 and H = <6> = {0, 6, 12}. Then G/H = {0 + H, 1 + H, 2 + H, 3 + H, 4 + H, 5 + H}. To illustrate how the group elements are combined, consider (5 + H) + (4 + H). This should be one of the six elements listed in the set G/H. Well, (5 + H) + (4 + H) = 5 + 4 + H = 9 + H = 3 + 6 + H = 3 + H, since H absorbs all multiples of 6.
and H = <6> = {0, 6, 12}. Then G/H = {0 + H, 1 + H, 2 + H, 3 + H, 4 + H, 5 + H}. To illustrate how the group elements are combined, consider (5 + H) + (4 + H). This should be one of the six elements listed in the set G/H. Well, (5 + H) + (4 + H) = 5 + 4 + H = 9 + H = 3 + 6 + H = 3 + H, since H absorbs all multiples of 6.
Example : A4 has no subgroup of order 6.
The group A4 of even permutations on the set {1, 2, 3, 4} has no subgroup H of order 6. To see this, suppose that A4 does have a subgroup H of order 6. We know that 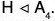 Thus, the factor group A4/H exists and has order 2. Since the order of an element divides the order of the group, we have (αH)2 = α2H = H for all α ∈ A4. Thus, a2 ∈ H for all α in A4. However, we observe that A4 has nine different elements of the form α2, all of which must belong to H, a subgroup of order 6. This is clearly impossible, so a subgroup of order 6 cannot exist in A4.
Thus, the factor group A4/H exists and has order 2. Since the order of an element divides the order of the group, we have (αH)2 = α2H = H for all α ∈ A4. Thus, a2 ∈ H for all α in A4. However, we observe that A4 has nine different elements of the form α2, all of which must belong to H, a subgroup of order 6. This is clearly impossible, so a subgroup of order 6 cannot exist in A4.
Theorem : The 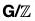 Theorem
Theorem
Let G be a group and let 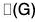 be the center of G. If
be the center of G. If 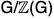 is cyclic, then G is Abelian.
is cyclic, then G is Abelian.
Proof. Suppose that G/Z(G) is cyclic. Then there is some aZ(G) ∈ G/Z(G) such that <aZ(G)> = G/Z(G).
Let x, y ∈ G We wish to show that xy = yx. It follows that there exist integers j, k such that xZ(G) = (aZ(G))i and yZ(G) = (aZ(G))k. So there exist z1, z2 ∈ Z(G) such that x = ajz1 and y = ak z2. Now consider their product:
xy = (aj z1)(ak z2)
= aj (z1ak)z2
= (aj ak)(z1z2)
= (ak aj)(z2z1)
= (ak z2)(ajz1) = yx
Note that in the third line above we are able to commute ak and z1 since z1 ∈ Z(G).
Similarly we are able to commute from line four to five.
Thus, we have shown that G is Abelian.
Theorem : 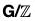 (G) ≈ Inn(G)
(G) ≈ Inn(G)
Let G be a group. For g ∈ G, let Tg : G → G be the automorphism (h)Tg = g-1hg. Let Inn(G) = {Tg : g ∈ G}. This is a subgroup of Aut(G) called the group of inner automorphisms. Show that Inn(G) is isomorphic to G/Z(G) where Z(G) = {g ∈ G : gh = hg for every h ∈ G} is the center of G.
OR
For any group G, 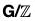 (G) is isomorphic to Inn(G).
(G) is isomorphic to Inn(G).
Proof. The map T : G → Aut(G) which sends g to Tg is a homomorphism with image Inn(G) and kernel Z(G). This implies Inn(G) ≈ G/Z(G) as claimed.
Theorem : Existence of Elements of Prime Order
Let G be a finite Abelian group and let p be a prime that divides the order of G. Then G has an element of order p.
Proof. Our proof uses two facts about finite cyclic groups. If G is cyclic and p divides IGI then G has an element of order p since G has exactly one (cyclic) subgroup for every divisor of |G|. If G = <a> has order m and an = e then min.
We proceed by induction on |G|. The case |G| = 1 is vacuous since p does not divide |G| in this case. Suppose m ≥ 1 and that theorem holds for all abelian groups of order less than or equal to m. Let G be an abelian group such that |G| ≤ m + 1 and suppose that p divides |G|. Then |G| > 1 so we may chose an a ∈ G with a ≠ e. If p divides |<a>| then <a>, hence G, has an element of order p.
Suppose p does not divide |<a>|. Since G is abelian H = <a> ≥ G. Since |G| = |G/H||H| and |H| > 1 it follows that p divides |G/H| and |G/H| < |G|. Since G/H is abelian, by our induction hypothesis there is an element bH ∈ G/H or order p. Let n = |<b>|. Then (bH)n = bnH = eH = H from which we deduce pin. Thus <b> has an element of order p.
Theorem : If N is normal subgroup of a finite group G, then 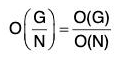
Proof : By definition, O(G/N) = the number of different right (left) cosets of N in G.
= the index of N is G
= (No. of elements in G/No. of elements in N)(O(G)/O(N)) [by Lagrange’s theorem]
Properties of Quotient Group
Every quotient of an abelian group is abelian but not conversely.Every quotient group of a cyclic group is cyclic but not conversely.
For example S3/A3 being a group of order 2 necessarily cyclic but S3 is not cyclic group.
GROUP ACTION
An action of a group G on a set S is a rule for combining an element g of G and an element s of S to get another element of S. In other words, it is a map G x S → S. For the moment we denote the result of applying this law to elements g and s by g*s. An action is required to satisfy the following axioms:
(a) id * s = s for all s in S. (Here id is the identity of G.)
(b) associative law: (gg’) *s = g*(g’*s), for all g and g’ in G and all s in S.
Given an operation of a group G on a set S, an element s of S will be sent to various other elements by the group operation. We collect together those elements, obtaining a subset called the orbit O3 of s:
Os = {s’ ∈ S | s’ = gs for some g in G}.
The orbits for a group action are equivalence classes for the equivalence relation s ~ s’ if s’ = gs, for some g in G.
So, if s ~ s’, that is, if s' = gs for some g in G, then the orbits of s and of s’ are the same.
Since they are equivalence classes the orbits partition the set S.
The stabilizer of an element s of S is the set of group elements that leave s fixed. It is a subgroup of G that we often denote by G3:
G3 = {g ∈ G | gs = s}.
Example: Let G be the group of nonzero real numbers under multiplication, and let S be the set of all vectors in 3-space. Thus S = {(a; b; c) | a, b, c ∈ R}. Then G acts on S via scalar multiplication. That is, g(a; b; c) = (ga; gb; gc) if g is a nonzero real number. Then for any vector v, we have 1* v = v and if g, h 2 G then (gh)v = g(h*v), since if v = (a; b; c) then (gh)v = (gha; ghb; ghc) = g(ha; hb; he) = g(hv).
Example : Let G be a group and S = G. Then G acts on S by left multiplication. That is, gs is defined to be the ordinary product of g and s in G. Associativity of multiplication in G and properties of the identity then show this is an action of G on S. This example leads to the proof of Cayley’s theorem.
Example : Conjugation, the operation of G on itself defined by (g, x) → gxg-1. The stabilizer of an element x of G for the operation of conjugation is called the centralizer of x. The orbit of x for conjugation is called the conjugacy class of x, and is often denoted by Cl(x). It consists of all of the conjugates gxg-1:
Cl(x)= {x’ ∈ G | x’ = gxg-1 for some g in G}.
Note :
- The centralizer C(x) of an element x of G contains x, and it contains the center Z(G).
- An element x of G is in the center if and only if its centralizer C(x) is the whole group G, and this happens if and only if the conjugacy class Cl(x) consists of the element x alone.
Since the conjugacy classes are orbits for a group operation, they partition the group. This fact gives us the class equation of a finite group:
If we number the conjugacy classes, writing them as C1,........... Ck, the class equation reads Order(G) = cardinality(C1) + cardinality(C2) + . . . + cardinality(Ck)
The numbers on the right side of the class equation divide the order of the group, and at least one of them is equal to 1 (∵ id. Has only 1 conjugate).
Example : In S3 id. has 1 conjugate. (1 2), (1 3), (2 3) are conjugates to each other (Since they have same cycle type) and (1 2 3) & (1 3 2) are conjugates. Thus, class equation of S3 = 1 + 2 + 3.
p-groups:
The class equation has several applications to groups whose orders are positive powers of a prime p. They are called p-groups.Theorem: The center of a p-group is not the trivial group.
Proof: Say that order(G) = pe with e > 1. Every term on the right side of the class equation divides pe, so it is a power of p too, possibly p° = 1. The positive powers of p are divisible by p. If the class C1 of the identity made the only contribution of 1 to the right side, the equation would read pe = 1 + ∑(multiples of p).
This is impossible, so there must be more 1’s on the right. The center is not trivial.
Theorem: Every group of order p2 is abelian.
Proof: Let G be a group of order p2. According to the previous theorem, its center Z is not the trivial group. So, the order of Z must be p or p2. If the order of Z is p2, then Z = G, and G is abelian as the proposition asserts. Suppose, that the order of Z is p, and let x be an element of G that is not in Z. The centralizer C(x) contains x as well as Z, so it is strictly larger than Z. Since |Z(x)| divides |G|, it must be equal to p2, and therefore Z(x) = G. This means that x commutes with every element of G, so it is in the center after all, which is a contradiction. Therefore, the center cannot have order p.
Simple group :
A group G is simple if it is not the trivial group and if it contains no proper normal subgroup- no normal subgroup other than <1> and G.
Example: An is a simple group ∀n ≥ 5. Any group of prime order is simple.
Sylow’s thorem :
Let G be a group of order n, and let p be a prime integer that divides n. Let pe denote the largest power of p that divides n, so that n = pem where m is an integer not divisible by p.
A Sylow p-subgroup is a p-group whose index in the group isn’t divisible by p.
Theorem 1: A finite group whose order is divisible by a prime p contains a Sylow p-subgroup.
Theorem 2: Let G be a finite group whose order is divisible by a prime p.
(a) The Sylow p-subgroups of G are conjugate subgroups.
(b) Every subgroup of G that is a p-group is contained in a Sylow p-subgroup.
Theorem 3: Let G be a finite group whose order n is divisible by a prime p. Say that n = pem, where p does not divide m, and let np denote the number of Sylow p-subgroups. Then np divides m and np is congruent to 1 modulo p: np = kp + 1 for some integer k > O.
Further, np is the index in G of the normalizer NG(H) for any Sylow p-subgroup H, hence np divides m.
Corollary: A group G has just one Sylow p-subgroup H if and only if that subgroup is normal.
Example: Let G be a group of order 35. According to the Third Sylow Theorem, the number of its Sylow7-subgroups divides 5 and is congruent 1 modulo 7. The only such integer is 1. Therefore, there is one Sylow 7-subgroup, say H, and it is a normal subgroup. For similar reasons, there is just one Sylow 5-subgroup, say K, and it is normal. The subgroup H is cyclic of order 7, and K is cyclic of order5. The intersection H ∩ K is the trivial group. Then G is isomorphic to the product group H X K. So, all groups of order 35 are isomorphic.to the product C7 X C5 of cyclic groups and to each other. The cyclic group of order 35 is one such group, so all groups of order 35 are cyclic.
|
98 videos|27 docs|30 tests
|
FAQs on Group Theory- IV - Mathematics for Competitive Exams
| 1. What is a group homomorphism? |  |
| 2. What are factor groups and how are they related to group homomorphisms? |  |
| 3. What is the significance of morphism in group theory? |  |
| 4. How can group actions be defined using group theory? |  |
| 5. What are some real-world applications of group theory? |  |

|
Explore Courses for Mathematics exam
|

|
 . then
. then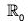
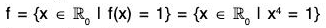
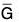 .
.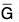 .
.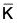 is a subgroup of
is a subgroup of 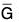 , then φ-1(
, then φ-1(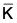 ) = {k ∈ G | φ(k) ∈
) = {k ∈ G | φ(k) ∈ 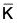 } is a subgroup of G.
} is a subgroup of G.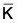 is a normal subgroup of
is a normal subgroup of 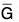 then φ-1(
then φ-1( .
.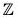 ∴ f is onto.
∴ f is onto.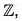
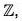 onto m
onto m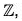 which is bijective.
which is bijective.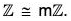
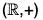 to group
to group  defined as
defined as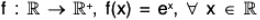
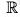
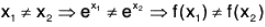
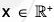 there exist log
there exist log 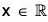 such that
such that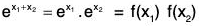
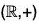 to the group
to the group 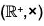 which is bijection. Hence f is an isomorphism.
which is bijection. Hence f is an isomorphism.