Group Theory | Engineering Mathematics - Civil Engineering (CE) PDF Download

Semigroup

A finite or infinite set ‘S′ with a binary operation ‘ο′ (Composition) is called semigroup if it holds following two conditions simultaneously −

• Closure − For every pair (a,b)∈S,(aοb) has to be present in the set S.
• Associative − For every element a,b,c∈S,(aοb)οc=aο(bοc) must hold.

Example

The set of positive integers (excluding zero) with addition operation is a semigroup. For example, S = {1,2,3,…}
Here closure property holds as for every pair (a,b)∈S,(a+b) is present in the set S. For example, 1+2=3∈S]
Associative property also holds for every element a,b,c∈S,(a+b)+c=a+(b+c). For example, (1+2)+3=1+(2+3)=5

Monoid

A monoid is a semigroup with an identity element. The identity element (denoted by e or E) of a set S is an element such that (aοe)=a, for every element a∈S. An identity element is also called a unit element. So, a monoid holds three properties simultaneously − Closure, Associative, Identity element.
Example
The set of positive integers (excluding zero) with multiplication operation is a monoid.
S={1,2,3,…}
Here closure property holds as for every pair (a,b)∈S,(a×b) is present in the set S.
[For example, 1×2=2∈S and so on]
Associative property also holds for every element a,b,c∈S,(a×b)×c=a×(b×c)
[For example, (1×2)×3=1×(2×3)=6 and so on]
Identity property also holds for every element a∈S,(a×e)=a
[For example, (2×1)=2,(3×1)=3 and so on]. Here identity element is 1.

Group

A group is a monoid with an inverse element. The inverse element (denoted by I) of a set S is an element such that (aοI)=(Iοa)=a, for each element a∈S. So, a group holds four properties simultaneously - i) Closure, ii) Associative, iii) Identity element, iv) Inverse element. The order of a group G is the number of elements in G and the order of an element in a group is the least positive integer n such that an is the identity element of that group G.

Examples
The set of N×N non-singular matrices form a group under matrix multiplication operation.
The product of two N×N non-singular matrices is also an N×N non-singular matrix which holds closure property.
Matrix multiplication itself is associative. Hence, associative property holds.
The set of N×N non-singular matrices contains the identity matrix holding the identity element property.
As all the matrices are non-singular they all have inverse elements which are also nonsingular matrices. Hence, inverse property also holds.

Abelian Group

An abelian group G is a group for which the element pair (a,b)∈G always holds commutative law. So, a group holds five properties simultaneously - i) Closure, ii) Associative, iii) Identity element, iv) Inverse element, v) Commutative.

Example
The set of positive integers (including zero) with addition operation is an abelian group.
G={0,1,2,3,…}
Here closure property holds as for every pair (a,b)∈S,(a+b) is present in the set S.
[For example, 1+2=2∈S and so on]
Associative property also holds for every element a,b,c∈S,(a+b)+c=a+(b+c)
[For example, (1+2)+3=1+(2+3)=6 and so on]
Identity property also holds for every element a∈S,(a×e)=a [For example, (2×1)=2,(3×1)=3 and so on]. Here, identity element is 1.
Commutative property also holds for every element a∈S,(a×b)=(b×a) [For example, (2×3)=(3×2)=3 and so on]

Cyclic Group and Subgroup

A cyclic group is a group that can be generated by a single element. Every element of a cyclic group is a power of some specific element which is called a generator. A cyclic group can be generated by a generator ‘g’, such that every other element of the group can be written as a power of the generator ‘g’.

Example
The set of complex numbers {1,−1,i,−i} under multiplication operation is a cyclic group.
There are two generators − i and –i as i¹=i, i²=−1, i³=−i, i⁴ = 1 and also (–i)¹=−i, (–i)²=−1, (–i)³=i,(–i)⁴=1 which covers all the elements of the group. Hence, it is a cyclic group.

Note: A cyclic group is always an abelian group but not every abelian group is a cyclic group. The rational numbers under addition is not cyclic but is abelian.
A subgroup H is a subset of a group G (denoted by H≤G) if it satisfies the four properties simultaneously − Closure, Associative, Identity element, and Inverse.
A subgroup H of a group G that does not include the whole group G is called a proper subgroup (Denoted by H<G). A subgroup of a cyclic group is cyclic and a abelian subgroup is also abelian.
Example
Let a group G={1,i,−1,−i}
Then some subgroups are H₁={1}, H₂={1,−1},

This is not a subgroup − H₃={1,i} because that (i)⁻¹=−i is not in H₃

Partially Ordered Set (POSET)

A partially ordered set consists of a set with a binary relation which is reflexive, antisymmetric and transitive. "Partially ordered set" is abbreviated as POSET.
Examples
The set of real numbers under binary operation less than or equal to (≤) is a poset.
Let the set S={1,2,3} and the operation is ≤
The relations will be {(1,1), (2,2), (3,3), (1,2), (1,3), (2,3)}

This relation R is reflexive as {(1,1), (2,2), (3,3)} ∈ R
This relation R is anti-symmetric, as
{(1,2), (1,3), (2,3)} ∈ R and {(1,2), (1,3), (2,3)} ∉ R
This relation R is also transitive as {(1,2), (2,3), (1,3)}∈R.
Hence, it is a poset.

The vertex set of a directed acyclic graph under the operation ‘reachability’ is a poset.

Hasse Diagram

The Hasse diagram of a poset is the directed graph whose vertices are the element of that poset and the arcs covers the pairs (x, y) in the poset. If in the poset x<y, then the point x appears lower than the point y in the Hasse diagram. If x<y<z in the poset, then the arrow is not shown between x and z as it is implicit.

Example

The poset of subsets of {1,2,3}={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}} is shown by the following Hasse diagram −

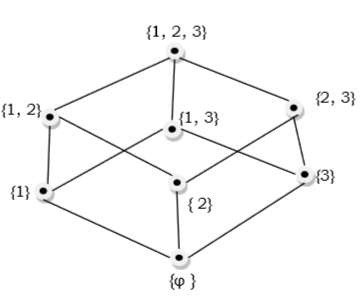
Linearly Ordered Set

A Linearly ordered set or Total ordered set is a partial order set in which every pair of element is comparable. The elements a, b ∈ S are said to be comparable if either a ≤ b or b ≤ a holds. Trichotomy law defines this total ordered set. A totally ordered set can be defined as a distributive lattice having the property {a∨b, a∧b}={a, b} for all values of a and b in set S.
Example
The powerset of {a,b} ordered by subseteq is a totally ordered set as all the elements of the power set P={∅,{a},{b},{a,b}} are comparable.
Example of non-total order set
A set S={1,2,3,4,5,6} under operation x divides y is not a total ordered set.
Here, for all (x,y)∈S, x|y have to hold but it is not true that 2 | 3, as 2 does not divide 3 or 3 does not divide 2. Hence, it is not a total ordered set.

Lattice

A lattice is a poset (L,≤) for which every pair {a,b} ∈ L has a least upper bound (denoted by a∨b) and a greatest lower bound (denoted by a∧b). LUB ({a,b}) is called the join of a and b. GLB ({a,b}) is called the meet of a and b.

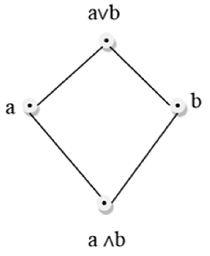
Example

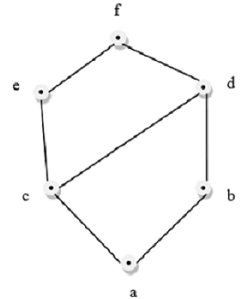
This above figure is a lattice because for every pair {a,b} ∈ L, a GLB and a LUB exists.

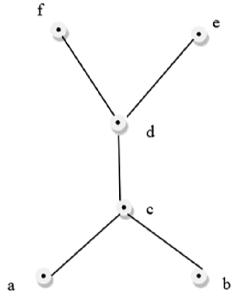
This above figure is a not a lattice because GLB(a,b) and LUB(e,f) does not exist.

Some other lattices are discussed below −

Bounded Lattice
A lattice L becomes a bounded lattice if it has a greatest element 1 and a least element 0.

Complemented Lattice
A lattice L becomes a complemented lattice if it is a bounded lattice and if every element in the lattice has a complement. An element x has a complement x’ if ∃x(x∧x′=0andx∨x′=1)

Distributive Lattice
If a lattice satisfies the following two distribute properties, it is called a distributive lattice.

• a∨(b∧c)=(a∨b)∧(a∨c)
• a∧(b∨c)=(a∧b)∨(a∧c)

Modular Lattice
If a lattice satisfies the following property, it is called modular lattice.
a∧(b∨(a∧d))=(a∧b)∨(a∧d)

Properties of Lattices

1. Idempotent Properties

• a∨a=a
• a∧a=a

2. Absorption Properties

• a∨(a∧b)=a
• a∧(a∨b)=a

3. Commutative Properties

• a∨b=b∨a
• a∧b=b∧a

4. Associative Properties

• a∨(b∨c)=(a∨b)∨c
• a∧(b∧c)=(a∧b)∧c

Dual of a Lattice
The dual of a lattice is obtained by interchanging the '∨' and '∧' operations.
Example
The dual of [a∨(b∧c)] is [a∧(b∨c)]