HOTS Questions: Be My Multiple, I’ll Be Your Factor | Mathematics for Class 5: NCERT PDF Download
Q1: Find the first four common multiples of the following :3,4 and 6.
(a) 72,78,84,90
(b) 12,24,36,48
(c) 24,30,36,42
(d) 8,12,16,21
Ans: (b)
Sol: Multiples of 3 = 3, 6, 9, 12, 15, 18..
Multiples of 4 = 4, 8, 12, 16, 20..
Multiples of 6 = 6, 12, 18, 36..
The first common multiple will be 12
And the next common multiples will be multiples of 12
Hence, first four common multiples of 3,4,6 are 12,24,36,48
Q2: State whether the following statement is True or FalseThe first six multiples of 13 are:
13,26,39,52,65,78.
(a) True
(b) False
Ans: (a)
Sol: First six multiples of 13 = 13 × 1, 13 × 2, 13 × 3, 13 × 4, 13 × 5, 13 × 6
i.e.
13, 26, 39, 52, 65, 78
The given statement is true.
Q3: State true or false: The common factors of 18 and 24 are 1,2,3,6.
(a) True
(b) False
Ans: (a)
Sol: Factors of 18 = 1, 2, 3, 6, 8, 9 and 18
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 and 24
Common factors are 1,2,3,6
Q4: Find the first six multiples of 17
(a) 17,51,85,102,119
(b) 34,76,102,119,340
(c) 34,51,68,102,170
(d) 17,34,51,68,85,102
Ans: (d)
Sol: First six multiples of 17=17,34,51,68,85 and 102.
Q5: Find the first four common multiples of the following : 3 and 4.
(a) 24,28,32,36
(b) 24,27,33,36
(c) 12,24,36,48
(d) 12,15,20,24
Ans: (c)
Sol: Multiples of 3 = 3, 6, 9, 12, 15, 18..
Multiples of 4 = 4, 8, 12, 16, 20..
The first common multiple will be 12
And the next common multiples will be multiples of 12
Hence, first four common multiples of 3,4 are 12, 24, 36, 48
Q6: State the following statement is True or False
The common factors of 75 and 50 are 1, 5, 25
(a) True
(b) False
Ans: (a)
Sol: Factors of 50 = 1, 2, 5, 10, 25 and 50
Factors of 75 = 1, 3, 5, 15, 25 and 75
Common factors are 1, 5, 25
Q7: The sum of the first five multiples of 6 is
(a) 90
(b) 60
(c) 30
(d) 120
Ans: (a)
Sol: First five multiple of 6 are
6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
6 × 5 = 30
Their sum will be 6 + 12 + 18 + 24 + 30 = 90
So correct answer will be option A.
Q8: Find the first four common multiples of the following :8 and 12.
(a) 24,48,72,96
(b) 24,36,48,56
(c) 24,32,40,48
(d) 48,72,96,120
Ans: (a)
Sol: Multiples of 8 = 8, 16, 24, 32,..
Multiples of 12 = 12, 24, 36, 48...
The first common multiple will be 24
And the next common multiples will be multiples of 24
Hence, first four common multiples of 8,12 are 24, 4 8, 72, 96
Q9: The number of common factors of 20,36 and 48 is:
Sol: Factors of 20 = 1, 2, 4, 5, 10, and 20
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 and 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
Hence, common factors of 20,36,48 are 1,2,4. So, total numbers of common factors is equal to 3.
Q10: Find the common factors of :
(a) 4,8 and 12
(b) 5,15 and 25
Sol:
(a) The factors of 4 are 1, 2, 4
The factors of 8 are 1, 2, 4, 8
The factors of 12 are 1, 2, 3, 4, 6, 12
Therefore, the common factors are 1, 2, 4
(b) The factors of 5 are 1,5
The factors of 15 are 1, 3, 5, 15
The factors of 25 are 1, 5, 25
Therefore, the common factors are 1, 5
Q11: Three common multiples of 18 and 6 are:
(a) 18,6,9
(b) 18,36,6
(c) 36,54,72
(d) None of the above
Ans: (c)
Sol: Common multiple means that the number should be divisible by both 18 and 6
So, the required numbers are 36, 54 and 72.
Hence, the answer is 36, 54, 72.
Q12: Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12,15 and 21
(ii) 17,23 and 29
(iii) 8,9 and 25
Sol:
Using prime factorisation method:
(i) 12, 15 and 21
Factor of 12 = 2 × 2 × 3
Factor of 15 = 3 × 5
Factor of 21 = 3 × 7
HCF (12, 15, 21) = 3
LCM (12, 15, 21) = 2 × 2 × 3 × 5 × 7 = 420
(ii) 17, 23 and 29
Factor of 17 = 1 × 17
Factor of 23 = 1 × 23
Factor of 29 = 1 × 29
HCF (17, 23, 29) = 1
LCM (17, 23, 29) = 1 × 17 × 23 × 29 = 11,339
(iii) 8, 9 and 25
Factor of 8 = 2 × 2 × 2 × 1
Factor of 9 = 3 × 3 × 1
Factor of 25 = 5×5 × 1
HCF (8, 9, 25) = 1
LCM (8, 9, 25) = 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1,800
Q13: Fill in the blanks
45 = 3 × 3 × 5, so ____, ____, _____and _____ are the factors of 45.
Sol: 45 = 3 × 3 × 5
so, 3, 5, 9,15 are factors of 45
Q14: Write the smallest 5 digit number. Express it in terms of its prime factor by a tree diagram.
Sol: We know that,
The smallest five-digit number is 10000.
Prime factor of 10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5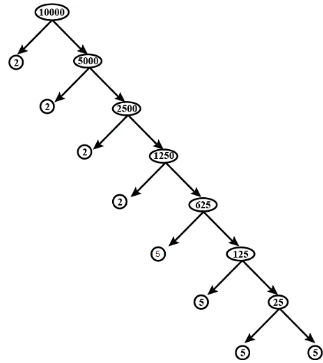
Q15: Write all the numbers less than 100 which are common multiples of 3 and 4.
Sol: The multiples of 3 less than 100 are
3, 6, 9, 12, 15, 18, 21, 24, 27,30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99
multiples of 4 less than 100 are
4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100
Therefore, the common multiples less than 100 are 12,24,36,48,60,72,84,96
Q16: Find the smallest number which is divisible by 85 and 119.
Sol: To find the smallest number which is divisible by 85 and 119, we have to take L. C. M. of 85 and119.
Prime Factors of 85 = 5 × 17
Prime Factors of 119 = 7 × 17
So,
L. C. M. of85 and 119 = 5 × 7 × 17
L. C. M. of 85 and 119 = 595
So,595 is the smallest number which is divisible by85 and119.
Q17: Write the first five multiples of 10 and 20. Highlight their common multiple and find their LCM.
Sol:
Multiples of 10:
10, 20, 30, 40, 50
Multiples of 20
20, 40, 60, 80, 100
Common multiples of 10 and 20 are 20,40
To find LCM of 20 and 40, we need to write these numbers in the form of product of their prime factors:
20 = 2 × 2 × 5 = 22 ×5
40 = 2 × 2 × 2 × 5 = 23 × 5
LCM(20, 40) = 2 × 2 × 2 × 5
= 40 Ans
Q18: Define multiple. Give four examples.
Sol: Multiple-It is a number which when multiplied with another number produces a given number.
For example:
- 30 is a multiple of 6 as 6 × 5 = 30
- 45 is a multiple of 5 as 5 × 9 = 45
- 21 is a multiple of 7 as 7 × 3 = 21
- 39 is a multiple of 13 as 13 × 3 = 39
Q19: Write all the numbers less than 100 which are common multiples of 3 and 4.
Sol: Multiples of 3 = 3, 6, 9, 12, 15….
Multiples of 4 = 4, 8, 12, 16, 20…
Common multiples=12, 24, 36, 48, 60, 72, 84, 96.
Q20: Write first five multiplies of the following number: 35
Sol: To find first 5 multiples of 35,
35 × 1 = 35
35 × 2 = 70
35 × 3 = 105
35 × 4 = 140
35 × 5 = 175
So, the first 5 multiples of 35 are 35, 70, 105, 140 and 175.
|
31 videos|192 docs|41 tests
|
















