Class 8 Maths Chapter 2 HOTS Questions - Linear Equations in One Variable
Q1: Half of a herd of deer are grazing in the field and three fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
(a) 65
(b) 36
(c) 72
(d) 74
Ans: c
Sol: Let the total no of deer be x
So, we have
Thus, x=72 deer in the herd.
Q2: It costs Rs. 10/kilometer to fly and Rs. 2/kilometer to drive. If one travels 200 km covering x km of the distance by flying and the rest by driving, then the cost of the trip is
(a) Rs. 2,000
(b) Rs. 24,000
(c) Rs.(8x+400)
(d) Rs. (12x+400)
Ans: c
Sol: Let distance travelled by flying is x km.
Hence, the distance travelled by driving =(200−x)km.
The cost of flying = Rs. 10 per km
Hence, the cost of flying x km =10 × x = 10x
The cost of driving = Rs. 2 per km
The cost of driving (200 − x) km =2 × (200 − x)= 400 − 2x
Hence, the total cost =10x + 400 − 2x = Rs.8x + 400
Q3: The present ages of a father and his son are in the ratio 7:3 and the ratio of their ages will be 2:1 after 10 years. Then, the present age of father (in years) is
(a) 42
(b) 56
(c) 70
(d) 77
Ans: c
Sol: Let the present ages of father and son be 7x and 3x.
After 10 years, their ages will be 7x+10 and 3x+10.
According to the question, we have
1(7x+10)=2(3x+10)
7x+10=6x+20
7x−6x=20−10
x=10
Then present age of father is 7x, i.e. 7×10=70 years.
Q4: The sum of three non-zero prime numbers is 100. One of them exceeds the other by 36. Then the largest number is
(a) 73
(b) 91
(c) 67
(d) 57
Ans: c
Sol: The sum of three prime numbers can only be even if one of the prime numbers is even, the only prime number that is even is 2.
So, the sum of the other two prime numbers must be 98.
x+x+36=98
⇒2x=62
⇒x=31
Numbers are 2,31 and 67.
The highest among them is 67.
Q5: The ages of Rahul and Haroon are in the ratio 5:7. Four years later the sum of their ages will be 56 years. What is the present age of rahul?
(A)14
(B) 18
(C) 20
(D) 11
Ans: c
Sol: Let the ages of Rahul and Haroon be 5x and 7x.
Four years later, their ages will be 5x + 4 and 7x + 4.
Given, the sum of their ages is 56.
∴ 5x + 4 + 7x + 4 = 56
12x = 56 − 8
12x = 48
∴x = 4
Therefore, age of Rahul will be 5x = 5 × 4 = 20 and that of Haroon will be 7x =7 × 4 = 28.
Thus, Rahul is 20 years and Haroon is 28 years old.
Q6: One of the two digits of a two digit number is three times the other digit. If you interchange the digits of this two-digit number and add the resulting number to the original number, you get 88. What is the original number?
(a) 26
(b) 12
(c) 43
(d) 16
Ans: a
Sol: Let one of the digits be x.
Then the other digit is 3x.
Original number =10x+3x=13x
Interchanged number =10(3x)+x=31x
⇒13x+31x=88
⇒44x=88
⇒x=2
The other digit =3x=3×2=6
Therefore the original number is 26.
Q7: Three consecutive integers are such that when they are taken in increasing order and multiplied by 2,3 and 4 respectively, they add up to 74. Find these numbers.
(a) 4,5,6
(b) 5,6,7
(c) 8,9,10
(d) 7,8,9
Ans: d
Sol: Let the consecutive integers be x,x+1,x+2
Given that they are taken in increasing order and multiplied by 2,3,4.
∴(x)2+3(x+1)+4(x+2)=74
2x+3x+3+4x+8=74
9x=74−11=63
∴x=7
Then, the numbers would be x=7,
x+1=7+1=8,
x+2=7+2=9.
So, the integers are 7,8,9.
Q8: The sum of three consecutive odd numbers is 57. Find the numbers.
(a) 17,19 and 21
(b) 19,15 and 25
(c) 13,17 and 26
(d) 21,13 and 29
Ans: a
Sol: Let the 3 consecutive odd numbers be x,x+2,x+4
x+x+2+x+4=57
3x=51
x=17
So the numbers are 17,19 and 21.
Q9: A student was asked to divide a number by 6 and add 12 to the quotient. He, however, first added 12 to the number and then divided it by 6, getting 112 as the answer. The correct answer should have been.
(a) 122
(b) 118
(c) 114
(d) 124
Ans: a
Sol: Let the number be x.
Then as per the given condition, the student was asked to find out the result of x/6 + 12...(1)
But he write it as x + 12/6 and got result as 112.
Therefore, x + 12/6 = 112
⇒x+12=112×6
⇒x=660
So, the number is 660
So, the correct result would be x/6 + 12 = 660/12 +12=122.
Hence, option A is correct.
Q10: The sum of the digits of a two digit number is 6 and its ten's digit is twice its unit digit. Find the number.
(a) 58
(b) 20
(c) 42
(d) 76
Ans: c
Sol: Let the unit's digit be x, then the ten's digit = 2x
Given sum of digits =6
⟹x+2x=6
3x=6
x=2
Ten's digit =2x=4
Required number =10(2x)+1(x)=10(4)+1(2)=42
Q11: Lakshmi is a cashier in a bank. She has notes of denomination of Rs. 20, Rs. 10 and Rs. 5. The ratio of number of these notes is 1:2:3. The total cash with Lakshmi is Rs. 1100. How many notes of Rs. 20 denomination does she have?
(a) 10
(b) 20
(c) 30
(d) None of the above.
Ans: b
Sol: Let the common multiple be x.
Therefore, the number of notes of each denomination are:
Rs. 20=1(x)=x notes
Rs. 10=2(x)=2x notes
Rs. 5=3(x)=3x notes
According to the given condition, total amount with Lakshmi is Rs. 1100.
20(x)+10(2x)+5(3x)=1100
⟹ 20x+20x+15x=1100
⟹ 55x = 1100
⟹ x = 20
Therefore, Lakshmi has 20 notes of Rs. 20 denomination.
Q12: Three friends, returning from a movie, stopped to eat at a restaurant. After dinner, they paid their bill and noticed a bowl of mints at the front counter. Sita took 1/3 of the mints, but returned four because she has a monetary pang of guilt. Fatima then took 1/4 of what was left but returned three for similar reasons. Eswari then took half of the remainder but threw two back into the ball. The ball has only 17 mints left when the raid was over. How many mints were originally in the bowl?
(a) 38
(b) 31
(c) 41
(d) 48
Ans: d
Sol: Number of mint before Esware has taken
Number of mint before Fatima has taken
Number of mint before Sita has taken
Hence there were 48 mints originally.
Q13: A container is 1/8 full of water. After 10 cups of water are added, the container is 3/4 full. What is the volume of the container, in cups?
(a) 15
(b) 16
(c) 40
(d) 20
Ans: b
Sol: Let the container full of water be 1/8x.
After 10 cups added, the container is 3/4 full.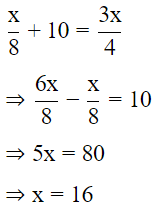
Therefore, volume of container in cups is 16.
Q14: A box contains x 50 paise coins, 2x one-rupee coins and 5x two-rupee coins. If the total value of these coins is Rs. 25 what is the value of x?
Ans: Total value of 50 paise coinss is 0.5 × x
Total value of one rupee coins is 1 × 2x
Total value of two rupee coins is 2 × 5x
Let R be the total value of given coins
R = 0.5 × x+1 × 2x+2 × 5x = 25
⇒ 0.5x + 2x + 10x = 25
⇒ 12.5x = 25
⇒ x = 25/12.5
⇒ x = 2
Q15: The sum of 3 consecutive multiples of 8 is 888. Find the multiples
Ans: Step 1: Find the integers.
Let, first multiple=x, Second multiple=x+8, third multiple=(x+8)+8=x+16
Now, Sum of multiple=21
⇒ x + (x + 8) + (x + 16) = 888
⇒ x + x + 8 + x + 16 = 888
⇒ x + x + x + 8 + 16 = 888
⇒ 3x + 24 = 888
⇒3x = 888 − 24
⇒ 3x = 864
⇒ x = 864/3
⇒ x = 288
Therefore, First integer = x = 288
Second integer = x + 8 = 296
Third integer = x + 16 = 304
Thus, the consecutive integers are 288, 296, 304
Q16: Construct 3 equations starting with x=−2.
Ans: x = −2
(1) x = −2
x + 2 = 0
(2) x − 2 = −2 − 2
x − 2 = −4
(3)2x = 2 × (−2)
2x = −4
Q17: Some ticket of 200 and some of 100, of a drama in theatre were sold. The number of tickets of 200 sold was 20 more than the number of tickets of 100. The total amount received by the theatre by sale of tickets was 37000. Find the number of 100 tickets sold.
Ans: Let the number of ticket of 100 sold be x
∴ Amount of ticket of 100 =100x
The number of tickets of 200 sold be 20+x
∴ Amount of tickets of 200 =200(20+x)
= 4000 + 200x
Total amount received = 37000
∴ 37000 = 100x + 4000 + 200x
= 300x + 4000
300x = 33000
Q18: In a scout camp, there is a food provision for 300 cadets for 42 days. If 50 more persons join the camp for have days will the provision last?
Ans: Initially there were 300 persons in the camp who had food for 42 days.
Now, with more 50 coming in, there are a total of 350 persons and say the food will now last for x day, then
300 × 42= 350 × x
Q19: In a study of bat migration habits, 240 male bats and 160 female bats have been tagged. If 100 more female bats are tagged, how many more male bats must be tagged so that 3/5 of the total number of bats in the study are male?
Ans: Once the 100 additional female bats are tagged, you’ll have 240 males and 260 females — a total of 500 bats.
Every male bat you tag adds not only to the number of male bats, but also to the total number of tagged bats. Your current male to total ratio is 240/500.
Let the number of male bats added be x
Then,
⇒ 3(500 + x) = 5(240 + x)
⇒ 1500 + 3x = 1200 + 5x
⇒ 300 = 2x
⇒ x = 150
Hence, 150 more male bats must be tagged.
Q20: A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (full weight 29.5 kg includes the empty cylinders tare weight of 15.3 kg.). If it is use with constant rate then it last for 24 days. Then the new cylinder is replaced Find the equation relating the quantity of gas in the cylinder to the days
Ans: From the given information, we may take two points (0, 14.2),(24, 0)
Since we are replacing the cylinder for every 24 days once, we have to consider this as periodic function.
f(x)= f(x + 24)
|
79 videos|408 docs|31 tests
|

|
Explore Courses for Class 8 exam
|

|

















