Class 8 Maths Chapter 9 HOTS Questions - Mensuration
Q1: The area of a trapezium is 34cm2 and the length of one of the parallel sides is 10cm and its height is 4cm. Find the length of the other parallel side in cm.
(a) 4
(b) 21
(c) 7
(d) 14
Ans: c
Sol: Area of trapezium = 1/2 (b1 + b2) × h = 34cm2
Where b1 = One parallel side of trapezium =10cm
b2 = Other parallel side of trapezium =b cm
h = height of trapezium = 4cm
Area of trapezium=34cm2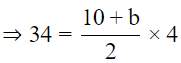
⇒ b + 10 = 17
⇒ b = 7cm
Q2: In a cylinder, radius is doubled and height is halved, curved surface area will
(a) halved
(b) doubled
(c) same
(d) four times
Ans: c
Sol: Step 1: Using the given condition find Curved Surface Area of Cylinder
Let us assume r is the radius of cylinder and h is the height of cylinder
∴ Curved surface area of cylinder is 2πrh.
If the radius is doubled and height is halved
⇒R = 2r, H = h/2
∴Curved surface area of the cylinder =2πRH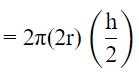
= 2πrh
Therefore, the curved surface area of the cylinder will be the same.
Q3: The number of dimensions, a solid has:
(a) 1
(b) 2
(c) 3
(d) 0
Ans: c
Sol: Step 1: Describing the dimensions in solid.
Dimension is a measurement of something in a particular direction. And as a solid has length, breadth and height.
Step 2: Finding the number of dimensions in solid.
So, the number of dimensions in solid=3.
Hence, correct option is C.
Q4: The area of a filed in the shape of a trapezium measures 1440m 2 . The perpendicular distance between its parallel sided is 24 m. If the ratio of the parallel sides is 5:3, the length of the longer parallel side is
(a) 45m
(b) 60m
(c) 75m
(d) 120m
Ans: c
Sol: Area of trapezium = 1/2 (sum of parallel sides) × height
= 1/2 (5x + 3x) × 24 = 1440.
Solving, we get x = 15 and length of longer side = 5 × 15 = 75m.
Q5: The shape of the top surface of a table is a trapezium. Find its area in cm2 if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
(A) 880cm2
(B) 88cm2
(C) 8800cm2
(D) 8.8cm2
Ans: c
Sol: Length of parallel sides is given as 1m = 100 cm and 1.2 m = 120 cm
Height (h) = 0.8 m = 80 cm
Area of trapezium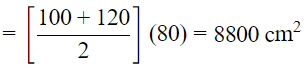
Q6: The ratio of the height of a circular cylinder to the diameter of its base is 1:2, then the ratio of the areas of its curved surface to the sum of the areas of its two ends is
(a) 1:1
(b) 1:2
(c) 2:1
(d) 1:3
Ans: a
Sol: Height : Diameter of cylinder = 1 : 2
Height : Radius of cylinder = 1 : 1
Curved surface area = 2πrh
Areas of two ends =2πr2
∴ their Ratio = 2πrh/2πr2 = 1 : 1
Q7: If the perimeter of one face of a cube is 20cm, then its surface area is
(A) 120cm2
(B) 150cm2
(C) 125cm2
(D) 400cm2
Ans: b
Sol: Perimeter of one face of a cube is 4a=20
⇒a=5 cm
Now the surface area will be 6a2
=6 × 5 × 5
=150cm2
Q8: If the radius of the base of a cylinder is 2 cm and its height 7 cm, then its curved surface is
(a) 44cm2
(b) 22cm2
(c) 88cm2
(d) 56cm2
Ans: c
Sol: Given, radius of cylinder =2 cm and height of cylinder =7 cm
∴ curved surface area of cylinder =2πrh
= 2π × 2 × 7
= 88cm2
Q9: If the curved surface of a cylinder be doubled the area of the ends, then the ratio of its height and radius is
(a) 2:3
(b) 1:1
(c) 2:1
(d) 1:2
Ans: c
Sol: Let the height and radius of the ends of a cylinder be h and r respectively.
Now Curved surface =2× Area of the ends
∴ 2πrh = 2 × (πr2 + πr2)
∴ h/r = 2/1
∴ h : r :: 2 : 1
Q10: A sphere has the same curved surface as the total surface area of cylinder of height 4 cm and diameter of base 8 cm. The radius of the sphere is
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 6 cm
Ans: c
Sol: The curved surface area of a sphere is same as the total surface area of a cylinder.
The height of the cylinder is 4 cm and the diameter of its base is 8 cm
To find out, The radius of the sphere.
Let the radius of the sphere be x cm.
We know that, total surface area of cylinder = 2πrh + 2πr2
We have r = d/2 = 4 cm and h = 4 cm
∴ Total surface area of the cylinder =2π(4)(4) + 2π(4)2
= 32π + 32π
= 64π
We also know that, curved surface area of a sphere = 4πr2
Hence, 4πx2 = 64π
⇒x2 = 16
∴ x = 4 cm
Hence, the radius of the sphere is 4 cm.
Q11: Find the area of four walls of a room having length, breadth and height as 8 m, 5 m and 3 m respectively. Find the cost of white-washing the walls at the rate of Rs. 15/m 2 .
Ans: It is given that length, breadth and height of a room are 8 m, 5 m and 3 m respectively.
Area of four walls of the room is: 2h(l+b)
A=2h(l+b)=2×3(8+5)=6×13=78 m 2
Area of the ceiling is:
A=l×b=8×5=40 m 2
Total area of the four walls and the ceiling of the room is 78+40=118 m 2
It is given that cost of white washing is Rs.15/m 2 , therefore,
Total cost of white washing is:
118×15=1770
Hence, the cost of white washing the walls is Rs.1770.
Q12: The length, breadth and height of a cuboid are in the ratio 5:3:2. If its volume is 35.937 m3 , find its dimension. Also find the total surface area of the cuboid.
Ans: Let the length, breadth, and height of the cuboid be 5x,3x and 2x respectively.
We know that the volume of the cuboid is l×b×h.
It is given that the volume of the cuboid is 35.937 m 3 , therefore,
35.937=5x × 3x × 2x
⇒30x3 =35.937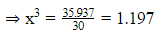

⇒x=1.06177
Therefore, the length l=5x=5×1.06177=5.309m, breadth b=3x=3.185m and height h=2x=2.124m
Now, the total surface area of cuboid is 2(lb+bh+hl), therefore, the total surface area with length 5.309 m, breadth 3.185 m and height 2.124 m is:
A=2[(5.309×3.185)+(3.185×2.124)+(2.124×5.309)]=69.9 m2
Q13: Length of the fence of a trapezium shaped field ABCD is 120 m. If BC=48 m, CD=17 m and AD=40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.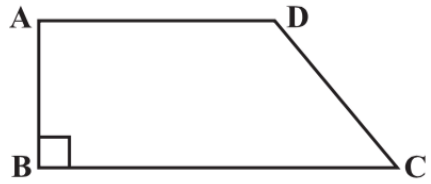
Ans: Length of fence of trapezium ABCD=AB+17+48+40
⇒120=105+AB
⇒AB=15 m
Area of trapezium
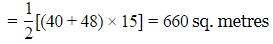
Q14: Find the difference in volume of two tanks of the following dimensions, in cm3 and in litres. Tank1; l=35 cm,b=20 cm,h=20 cm; Tank 2: l=40 cm,b=24 cm,h=24 cm.
Ans: V1=35×20×20=400×35=14000=14litre
V2=40×24×24=23040=23.04litre
V2−V1=23.04−14
=9.04litre
Q15: From a solid wooden cube of sides 14 cm a biggest hemispherical depression is carved out. What is the total surface area of the remain solid?
Ans: Total surface area of remaining solid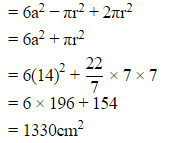
Q16: A box with a lid is made of wood which is 3 cm thick. Its external length, breadth and height are 5 cm,39 cm and 30 cm respectively. Find the capacity of the box. Also find the volume of wood used to make the box.
Volume =(56−6)×(39−6)×(30−6)
=39600cm3
Volume of wood =3cm × SA of external box
⇒3×2(56×39+56×30×39×30)
⇒30204cm3 .
Hence, the answer is 30204cm3 .
Q17: An open box of length 1.5m, breadth 1m, and height 1m is to be made for use on a trolley for carrying garden waste. How much sheet metal will be required to make this box? The inside and outside surface of the box is to be painted with rust proof paint. At a rate of 150 rupees per sqm, how much will it cost to paint the box?
Ans: Surface Area =2(l*b+b*h+h*l)
Surface Area =2(1.5*1+1*1+1*1.5)
Surface Area =2(1.5+1+1.5)
Surface Area =2*4=8m2 answer
cost of paint the box =8*150=1200rupees
Q18: A matchbox measures 4cm×2.5cm×1.5cm. What will be the volume of a packet containing 12 such boxes?
Ans: VOLUME: The space occupied by an object is called the volume of the particular object.
Volume is always measured in cubic unit.
Given: Dimensions of the matchbox =4 cm×2.5 cm×1.5 cm
So, l=4 cm, b=2.5 cm and h=1.5 cm
Volume of cuboid =(l×b×h)
Volume of one matchbox = Volume of cuboid
Volume of one matchbox =4×2.5×1.5
=15 cm3
Volume of a packet containing 12 such boxes =12× volume of one match box
=(12×15) cm 3 =180 cm3
Hence, the volume of a packet containing 12 such boxes =180 cm3
Q19: The length of parallel sides of trapezium is 14 cm and 6 cm and its height is 5 cm. Its area will be
(a) 50cm2
(b) 100cm2
(c) 210cm2
(d) 10cm2
Ans: Given: Length of parallel sides of trapezium =14 cm and 6 cm
Height of trapezium =5 cm
To find: Area of trapezium.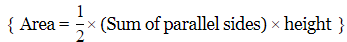
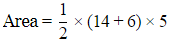
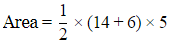
Area =50 cm2
Q20: The dimensions of a rectangular box are in the ratio of 2:3:4 and the difference between the cost of covering it with sheet of paper at the rates of Rs. 8 and Rs. 9.50 per m2 is Rs. 1248. Find the dimensions of the box,
Ans: Let l=2x,b=3x and h=4x in metres.
Surface area =2(lb+bh+lh)=52 x2m2
Difference of costs at the two rates =Rs{52 x 2 ×9.5−52 x 2 ×8}=78 x 2
∴78 x 2 =1248⇒x=4
dimensions of the box are l=8,b=12,h=16
|
79 videos|408 docs|31 tests
|

|
Explore Courses for Class 8 exam
|

|

















