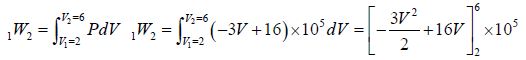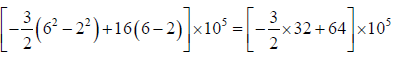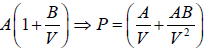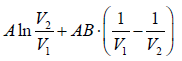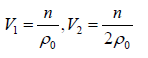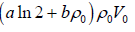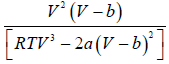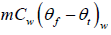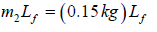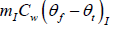Heat & Work Done | Kinetic Theory & Thermodynamics - Physics PDF Download
Heat Exchanged (Q)
When two systems with different temperatures are put in contact, heat flows spontaneously from the hotter to the colder system. There are different parameter which is helpful to determine Heat exchange of system mainly comprises Fluid and Gas.
Specific Heat
Heat capacity of a body is numerically equal to quantity of heat required to raise its temperature by 1 unit
C = 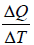
The specific heat of a material is numerically equal to quantity of heat required to raise the temperature of unit mass of that materials through 1 unit
C = 
Heat Capacity of Ideal Gas
If f is degree of freedom of Ideal gas, then from equi-partition law of energy, the total sum of energy is equivalent to sum of kinetic energy associated with each degree of freedom
Molar Heat Capacity
Molar heat capacity is defined as the energy required to raise the temperature of one mole of Ideal gas by one Kelvin at constant volume.
U = 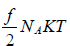 , where NA is Avogadro number
, where NA is Avogadro number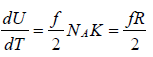
Cv = Rf/2, for ideal gas
Cp = Cv + R = 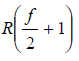
γ is defined as ratio of heat capacity at constant pressure to heat capacity at constant
volume.
γ = 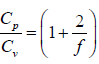
Latent Heat
The heat required to convert a solid into a liquid or vapor, or a liquid into a vapor, without change of temperature. Latent heat can be understood as heat energy in hidden form which is supplied or extracted to change the state of a substance without changing its temperature. Examples are latent heat of fusion and latent heat of vaporization involved in phase changes, i.e. a substance condensing or vaporizing at a specified temperature and pressure. A specific latent heat L expresses the amount of energy in the form of heat Q required to
completely effect a phase change of a unit of mass (m) , usually 1kg , of a substance as
an intensive property, then
Q = mL
Work Done during Process
Suppose due to heat supplied Q to a system, the system expands and applies pressure P on piston of area A while is displaced by dx
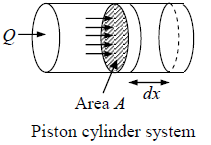
Work done by system 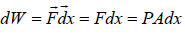
Total work W = ∫PAdx or W = ∫PdV where Adx = dV volume swept by piston.Work done when process is occurred between A to B is the area under the PV curve i.e. 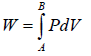
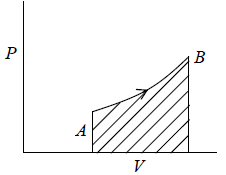
If work is done by the system, it has positive sign and if work is done on the system, it has negative sign.
valid for a reversible pressure only as integration can be done only for a continuous path. Otherwise W = PΔV irreversible process.
Sign convention:
Work done(∂W ) by the system is positive but work done on the system is negative, Heat (∂Q) absorbed by system is positive and heat rejected by the system is negative.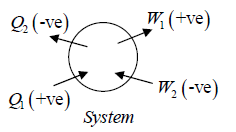
Example 3: A non flow quasi – static (reversible) process occurs for which P = (-3V + 16)bar, where V is volume in m3 . What is the work done when V changes from 2m3 to 6m3?
P = (-3V + 16)bar = (3V + 16)x105N/M2
=
=[-48 + 64]x105 = 16 x 105 Nm or J
Example 4: The equation of state for one mole of a non-ideal gas is given by  , where the coefficient A and B are temperature dependent. If the volume changes from V1 to V2 in an isothermal process, find the work done by the gas.
, where the coefficient A and B are temperature dependent. If the volume changes from V1 to V2 in an isothermal process, find the work done by the gas.
PV =
W==
Example 5: The pressure P of a fluid is related to its number density ρ by the equation of state P = aρ + bρ2 where a and b are constants. If the initial volume of the fluid is V0 , Find the work done on the system when it is compressed, so as to increase the number density from an initial value of ρ0 to2ρ0.
P = aρ + bρ2 ⇒ P =ρ = n/V
W =where
⇒ W ==
, n = ρ0V0
Work done on the system = -W =
Thermodynamical coefficient for Gases
Coefficient of Volume Expansion or Expansivity(α) the ratio of the increase of length, area, or volume of a body per degree rise in temperature to its length, area, or volume, respectively, at some specified temperature, commonly 0°C, the pressure being kept constant also called expansivity.
α = 
Isothermal Elasticity
The Ratio of the change in pressure acting on volume to the fractional change in volume. Isothermal Elasticity can be compare to Bulk modulus of Ideal gases
Isothermal compressibility
The inverse of Isothermal Elasticity is identified as Isothermal compressibility

Adiabatic Elasticity
The Ratio of the change in pressure acting on volume to the fractional change in volume in such a way that heat is not allowed to exchanged
Adiabatic compressibility
The inverse of Adiabatic elasticity is identified is Adiabatic compressibility
βs = 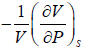
Example 6: Find the isothermal compressibility βT of a van der Waals gas which is given by equation of state 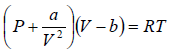 as a function of volume V at temperature T .
as a function of volume V at temperature T .
Note: By definition, βT = 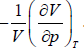
We know bulk modulus of a gas is given by
van der Wall equation =
(i)
If process is isothermal: T = constant
= 0
= 0
dP/dV =
βT =
=
(ii)
Put values of P from (i) in (ii)
βT =
Conservation of energy base of first law of thermodynamics
Energy can neither be created nor destroyed; rather, it can only be transformed or transferred from one form to another.
Consider a system of Ideal gas with boundary in which the process is reversible
Case -1 -when boundary of system is rigid
When system is rigid volume cannot be changed, when heat energy Q is supplied to a
system, the activity of its constituent particles increases because of this energy.
The level of increased energy is measured in terms of internal energy of the system
particles. So, Q = 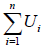 , Ui is internal energy of ith system particles. The level of activity is measured in terms of temperature. If body is cooled, the reverse of this happens. In nutshell we can say that Q has been converted into U or vice versa. So energy is conserved.
, Ui is internal energy of ith system particles. The level of activity is measured in terms of temperature. If body is cooled, the reverse of this happens. In nutshell we can say that Q has been converted into U or vice versa. So energy is conserved.
In this case heat is converting into internal energy and vice versa .
Case -2 when when boundary of system is not rigid and made of conductor
Suppose heat supplied Q into a system, then pressure developed on such that boundary
of system expands by volume dV then mechanical work done is given by W = ∫PdV. The heat exchanged Q is equal to work done W similarly if boundary of system contracted then work done on the system and Heat will flow out of system. In this case heat is converting into mechanical energy and vice versa.
Case 3: When boundary not rigid but made of insulator.
In this case heat cannot be exchanged but if boundary of system is expand such that it cool the gases so internal energy will decrease similarly if boundary will compressed then
temperature of gas increase so internal will increased energy
Example 7: When 0.15kg of ice at 0oC is mixed with 0.3kg of water at 50oC in a container, the resulting temperature is 6.7oC . Calculate the heat of fusion of ice.
(Cwater = 4186Jkg-1K-1)
Heat lost by water
= (0.30kg)(4186Jkg-1K-1)(50oC -0oC ) = 54376.14J
Heat required to melt ice =
Heat required to raise temperature of ice water to final temperature =
= (0.15kg)(4186Jkg-1K-1)(6.7oC -0oC ) = 4206.93J
Heat lost = Heat gained
54376.14J = (0.15kg)Lf + 4206.93J ⇒ Lf = 3.34 x 105Jkg-1
Example: If one mole of a monatomic gas (γ = 5 / 3) is mixed with one mole of a diatomic gas (γ =7 / 5) , then value of γ for the mixture. Assume volume of container is constant and no heat can be exchanged
(b): For a monatomic gas Cv1= 3R/2 for diatomic gas, Cv2 = 5R/2
n1 =1,n2 =1
From conservation of energy n1CV1T n2CV2T = (n1 + n2 )CvT
Cv =
= 2R
CP = Cv + R = 2R + R = 3R
γmixture =
= 1.5
|
6 videos|20 docs|32 tests
|
FAQs on Heat & Work Done - Kinetic Theory & Thermodynamics - Physics
| 1. What is the concept of heat exchange in thermodynamics? |  |
| 2. What is latent heat and how does it affect thermodynamic processes? |  |
| 3. How is work done during a thermodynamic process calculated? |  |
| 4. What is the thermodynamic coefficient for gases and how is it related to the ideal gas law? |  |
| 5. How does adiabatic elasticity differ from isothermal elasticity in thermodynamics? |  |